
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Условное математическое ожидание
Свойство 3.
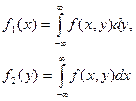
Для того, что бы охарактеризовать зависимость между составляющими двумерной случайной величины введем понятие условия распределения. Рассмотрим дискретную случайную величину (x,y). Пусть возможное значение составляющих 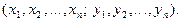
Определение. Условным распределением составляющей х при 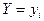 называется совокупность условных вероятностей
называется совокупность условных вероятностей 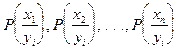 , вычесленная в предположении, что событие уже наступило. Аналогично определяется условное распределение составляющей Y.
, вычесленная в предположении, что событие уже наступило. Аналогично определяется условное распределение составляющей Y.
Определение.Пусть 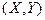 – непрерывная дискретная случайная величина с условной плотностью
– непрерывная дискретная случайная величина с условной плотностью 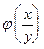 распределение составляющей х при данном значении
распределение составляющей х при данном значении 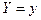 называется отношение плотности совместного распределения
называется отношение плотности совместного распределения 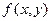 системы
системы 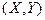 к плотности распределения
к плотности распределения  составляющей Y.
составляющей Y.
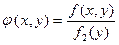 (*)
(*)
Важной характеристикой условного распределения вероятности является условие математического ожидания.
Определение. Условным математическим ожиданием дискретной случайной величины Y, при Х=х (х–определенное возможное значение Х) называется произведение возможных значений Y на их условные вероятности.
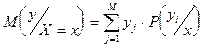 .
.
Для некоторых величин:
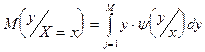
где 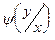 –это условная плотность случайной величины Y при Х=х.
–это условная плотность случайной величины Y при Х=х.
Условное математическое ожидание 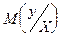 есть функция от f(x), которая называют функцией регрессии Y на Х. Аналогично определяют условное мат. ожидание случайной величины Х и функции регрессии Х на Y:
есть функция от f(x), которая называют функцией регрессии Y на Х. Аналогично определяют условное мат. ожидание случайной величины Х и функции регрессии Х на Y: 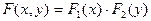 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности). Ее свойства | | | Зависимые и независимые лучайные величины |
Дата добавления: 2014-02-26; просмотров: 1112; Нарушение авторских прав

Мы поможем в написании ваших работ!