Тема 3. Нестационарная теплопроводность в телах простейшей формы

Методы решения краевой задачи в теории теплопроводности

Все методы решения краевой задачи теории теплопроводности можно разделить на две большие группы. К первой группе относят методы, использующие современные средства математического анализа, вычислительной математики и вычислительной техники, поэтому их называют теоретическими методами. Во вторую группу включены методы, при использовании которых, температурное поле находят в результате проведения эксперимента. Поэтому их называют экспериментальными методами.

Экспериментальные методы делятся на методы теории подобия и методы аналогий. По методу теории подобия температурное поле находят экспериментально на модели, в которой реализуется процесс той же физической природы, что и в объекте моделирования. По методу аналогий исследование процесса теплопроводности заменяется исследованием процесса другой физической природы, который протекает аналогично процессу теплопроводности. Эта аналогия проявляется в одинаковых по форме записи дифференциальных уравнениях переноса, относящихся к разным физическим явлениям.

Теоретические методы можно подразделить на аналитические, численные, численно-аналитические методы.

При использовании аналитических методов решение получают в виде конечной формулы или бесконечного ряда. Различают точные аналитические методы (метод разделения переменных или метод Фурье, метод интегральных преобразований, метод конформных отображений и др.) и приближенные аналитические методы (различные формы вариационных методов, метод подстановок и др.). Точные аналитические методы можно применять только к линейным задачам теории теплопроводности.

При использовании численных методов решение задачи получают в виде набора значений температур в дискретных точках пространства в дискретные моменты времени. В настоящее время для методами решения задач теплообмена наиболее часто используют метод сеток и метод конечных элементов.

Методы, которые используют аналитические решения для получения значений температур в дискретных точках пространства в дискретные моменты времени, называются численно-аналитическими (метод граничных элементов, метод R-функций, метод дискретного удовлетворения краевых условий и др.).

В результате решения задачи нестационарной теплопроводности находят температурное поле 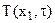, изменяющееся в пространстве и во времени. Точные аналитические решения дифференциального уравнения теплопроводности для тел простейшей формы с граничными условиями I, II и III родов приведены в методических указаниях "Нестационарная теплопроводность" №1684. Для удобства инженерных расчетов аналитическое решение при ГУ III рода представлено в виде графиков – номограмм, которые для тел простейшей формы также приведены в той же методичке №1684. Поэтому далее рассмотрим постановку задачи и алгоритм определения температурного поля с помощью номограмм.

Дата добавления: 2014-03-11; просмотров: 505; Нарушение авторских прав

Мы поможем в написании ваших работ!