Пуассоновский (простейший) поток запросов

Стационарный ординарный поток без последействия называют простейшим.

Он задается набором вероятностей P_i(t) поступления i требований впромежутке длиной t.

Можно показать, что при этих предположениях формула для P_i(t) дается формулой Пуассона (Poisson):

.

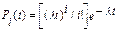Проанализируем основные характеристики пуассоновского потока. Рассмотрим отношение P_i(t)/P_i-1(t). При i ≤ λt вероятность растет, а при обратном соотношении – убывает. Графики функции распределения Пуассона в зависимости от величины λt для различных значений k приведены на рис. 1.

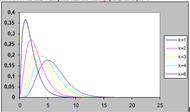
Рис. 1. Графики Пуассоновского распределения в зависимости от lt для различных k.

Наряду с распределением P_i(t) используют вероятности поступления не менее i требований в интервал t или не более i требований за время t:

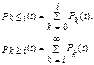
Если рассмотреть закон распределения вероятностей промежутка между поступлением соседних требований τ, то можно показать, что

.

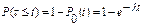Дифференцируя, получаем плотность распределения вероятностей: .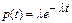

Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно

,

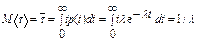а дисперсия и среднеквадратическое отклонение соответственно будут равны:

,

.

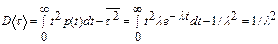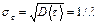Определим математическое ожидание и дисперсию числа требований за промежуток t :

,

.

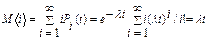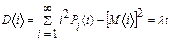Одним из важных свойств пуассоновского потока является аддитивность.

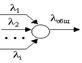Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока _.

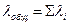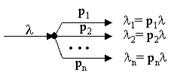При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p_i (Sp_i =1) поступает на i-тоенаправление, поток i направления будет также пуассоновским с интенсивностью lp _i.

Дата добавления: 2014-03-13; просмотров: 476; Нарушение авторских прав

Мы поможем в написании ваших работ!