Определение перемещений энергетическими методами

Рассмотренные выше методы неприменимы для балок с криволинейной осью и для рам. Более универсальными в этом смысле являются энергетические методы. Наиболее популярным является метод Мора (интеграл Мора).

Согласно методу Мора рассматриваются два состояния системы (балки, рамы): грузовое и единичное.

Грузовое состояниеобусловлено действием на систему заданной внешней нагрузки. Возникающие при этом силовые факторы и их эпюры называются грузовыми.

Единичное состояниеобусловлено действием на систему единичной обобщённой нагрузки, приложенной по направлению искомого перемещения. Возникающие при этом силовые факторы и их эпюры называются единичными. Под обобщённой нагрузкой понимается либо сосредоточенная сила, либо сосредоточенный момент. Обобщённой нагрузке соответствуют обобщённые перемещения.Сосредоточенной силе соответствует линейное перемещение. Сосредоточенному моменту соответствует угол поворота сечения.

Пренебрегая перемещениями, связанными с деформацией сдвига ввиду их малости по сравнению с деформацией изгиба интеграл Мора для случая прямого плоского изгиба запишется в виде:

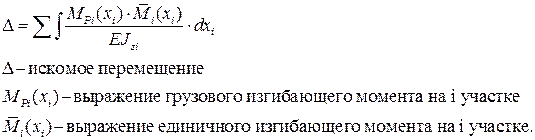
Во всех энергетических методах знак результата означает:

Знак « + » - искомое перемещение совпадает по направлению с приложенной единичной нагрузкой.

Знак «-» - искомое перемещение противоположно по направлению приложенной единичной нагрузке.

Графический способ вычисления интеграла Мора – способ Верещагина.

Формула Верещагина записывается в виде:

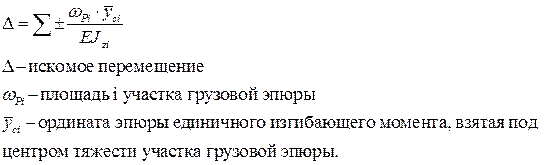
Знак « + » - когда площадь грузовой эпюры совпадает по направлению с эпюрой от единичной нагрузки.

Знак «-» - когда площадь грузовой эпюры противоположна по направлению эпюре от единичной нагрузки.

Минимальное количество слагаемых в формуле Верещагина равно количеству участков эпюры единичного момента. Если границы эпюры грузового момента не совпадают с границами эпюры единичного момента, то грузовую эпюру необходимо дополнительно разбить по границе единичной эпюры.

Если имеются трудности с определением площадей и положений центров тяжести участков грузовых эпюр, то для вычисления интеграла Мора

Рационально использовать формулу Симпсона-Корнаухова:

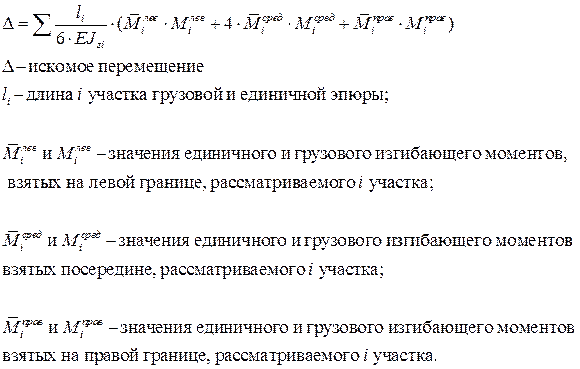
Формула Симпсона - Корнаухова справедлива для конструкций с прямыми участками (для балок и рам). Грузовая эпюра должны быть линейна или является параболой не выше второй степени.

Отметим, что перемещения, определённые с помощью дифференциального уравнения изогнутой линии балки и с помощью энергетического метода получаются одинаковыми по абсолютной величине.

Для оценки величины полученной деформации вычисляют значение перемещения 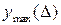балки. Значения 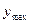приведены в учебниках по сопротивлению материалов для различных случаев нагружения балок.

Величина прогиба нужна для проверки условия жёсткости: максимальный прогиб не должен превышать допускаемого. Можно воспользоваться значением 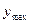из справочника при вычислении значения приложенных нагрузок.

Пример: Вычислим значение реакции средней опоры для двухпролётной неразрезной балки с консолями , где

l – длина пролёта;

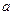– длина консоли;

Р – нагрузка.

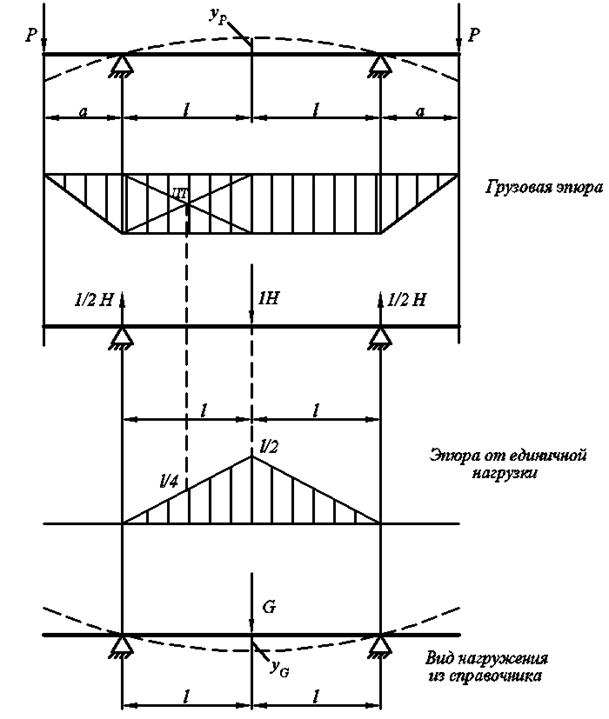
Для вычисления величины прогиба 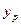от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями. Для вычисления величины прогиба 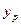от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями.

Для вычисления величины прогиба 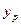от сил Р воспользуемся методом Верещагина:

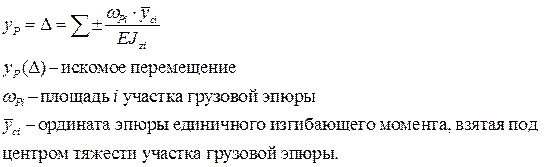
Для этого нужно площадь грузовой эпюры умножить на ординату эпюры от единичной нагрузки, находящуюся на одной линии с центром тяжести площади грузовой эпюры, получаем:

,

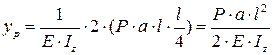где 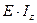– жёсткость сечения.

Значение величины прогиба 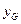, возникающее от действия силы 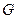, приложенной в середине, возьмём из справочника по сопротивлению материалов:

.

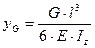Приравнивая величины прогибов ,

получим: 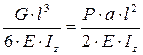, следовательно: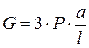

Лекция № 5 « Сложное напряжённое состояние. Гипотезы прочности»

Сложным называется напряжённое состояние при котором на трех взаимно-перпендикулярных площадках действуют нормальные и касательные напряжения.

Напряжение, перпендикулярное площадке называется нормальным и вычисляется по формуле:

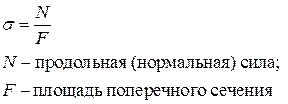
Напряжение, расположенное на площадке, называется касательным и вычисляется по формуле:

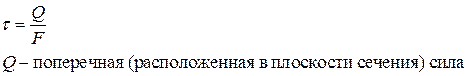
Оказывается при любом сложном напряжённом состоянии тела через каждую его точку можно провести три взаимно-перпендикулярные площадки, где будут отсутствовать касательные напряжения. Только нормальные.

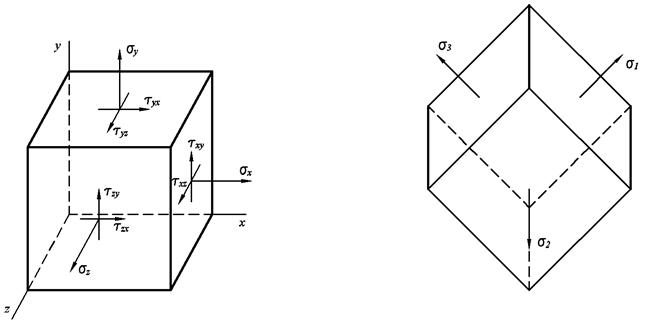
При этом они распределяются следующим образом .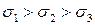

Например: 200 МПа > 150 МПа > 120 МПа.

; ; ,

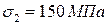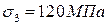С учётом знака:

; ;

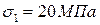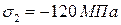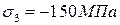
Площадки, на которых действует только один вид напряжений, называются главными.

В зависимости от количества главных напряжений, приложенных к главным площадкам, различают три вида напряжённого состояния в точке:

1. Все 3 главных напряжения не равны нулю. Такое напряжённое состояние называется объёмным (например, подводная лодка под водой).

2. Если одно из главных напряжений равно нулю. Такое напряжённое состояние называется плоским. Например, вал. В этом случае он испытывает сжатие по двум направлениям, при условии, если шкив не вращается. При вращении шкива появится ещё касательное напряжение, действующее на вал.

3. Одно главное напряжение не равно нулю. Такое напряжённое состояние называется линейным. Простое растяжение или сжатие.

В случае сложного напряжённого состояния необходимо привести все действующие напряжения к линейному состоянию и рассматривать сложное напряжённое состояние как простое линейное растяжение или сжатие.

Сначала определим главные напряжения для плоского напряжённого состояния, избавившись от касательных напряжения:

Для этого вырежем у детали элемент. Напряжения 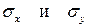не будут главными, так как действуют ещё и касательные напряжения.

Существуют формулы, позволяющие переходить от не главных напряжений к главным напряжениям:

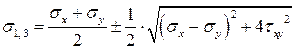
Получили плоское напряжённое состояние.

Для проверки прочности достаточно сравнить наибольшее главное 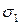или модуль главного напряжения 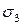(при отрицательном значении) с допускаемым .

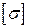Если 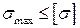, значит прочность будет обеспечена

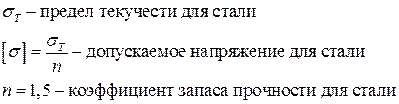
Для хрупких материалов максимальные отрицательные значения сравнивают с допускаемым значением на сжатие, положительные на растяжение. При этом коэффициент запаса прочности п=2.

Рассмотрим вторую обратную задачу:

При известных главных напряжениях нужно найти нормальные и касательные напряжения в любой точке наклонного сечения.

Дано: 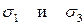, напряжения действуют по двум взаимно перпендикулярным направлениям - плоское двухосное напряжённое состояние.

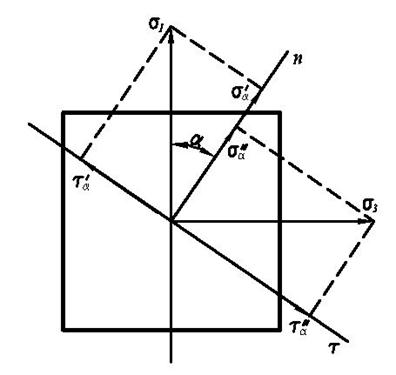
Найти: 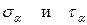, нормальное и касательное напряжения, действующие в наклонном сечении.

Рассмотрим отдельно действие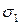

Напряжения в наклонных сечениях от действующего напряжения 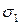будут равны:

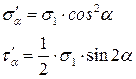
Рассмотрим действие напряжения 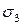, действующее к наклонному сечению под углом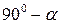

Напряжения в наклонных сечения от действующего напряжения 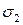будут равны:

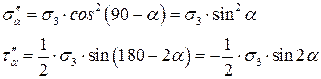
Если сложить все нормальные и касательные напряжения в наклонном сечении, получим полные нормальные и касательные:

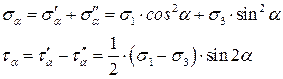
Если в формулу для 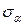подставить значение 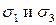, то при любом значении угла 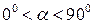, напряжение в наклонном сечении -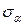всегда будет меньше 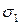, так как 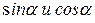всегда меньше единицы, а в число меньшее единицы в квадрате будет ещё меньше.

Это значит, что из всех напряжений главные самые большие.

Рассмотрим случай действия всех главных напряжений 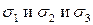. Объёмное напряженное состояние. Если в направлении действия 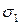будет происходить растяжение, то в направлении 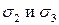будет происходить сжатие. Можно привести к обобщённому закону Гука.

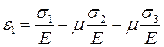
или

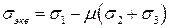, если

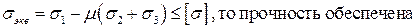
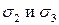уменьшают действие .

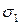Аналогично для относительных деформаций 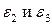можно записать:

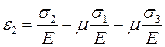
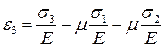
Из всех относительных деформаций 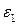будет самая большая.

Если 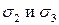будут действовать внутрь, то будет знак « + ».

Дата добавления: 2014-03-13; просмотров: 1118; Нарушение авторских прав

Мы поможем в написании ваших работ!