
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Управление инвестиционным портфелем
Приведенные выше критерии выбора инвестиций в случае одиночных активов были распространены Г.Марковицем на инвестиционные портфели. Ниже будут рассмотрены основные принципы формирования инвестиционного портфеля (детальное изложение современных подходов к формированию инвестиционного портфеля и управлению портфельными инвестициями выходит далеко за пределы базового курса финансового менеджмента и рассматривается в специальных курсах).
Очевидно, что, формируя инвестиционный портфель, инвестор будет объективно руководствоваться принципом оптимизации соотношения между риском и доходностью. Как уже отмечалось выше, это означает, что при любом заданном уровне риска инвестор будет стремиться к максимизации ожидаемой доходности, а при заданной ожидаемой доходности – стремиться к минимизации риска. Портфели, удовлетворяющие сформулированным условиям, носят название эффективных. Совокупность эффективных портфелей представляет собой выпуклую6 кривую BCDE на Рис. 3.7 и носит название набора эффективных портфелей или границы эффективности. Все остальные портфели, находящиеся внутри фигуры ABCDEGH (помечены цифрой 2) представляют собой набор возможных портфелей (допустимое множество). Вне этой фигуры лежат портфели, не являющиеся возможными.
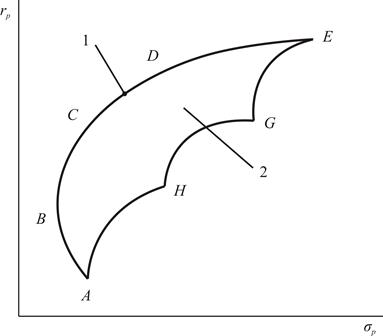
 Рис. 3.7. Эффективный набор и допустимое множество портфелей.
Рис. 3.7. Эффективный набор и допустимое множество портфелей.
Технически построение кривой границы эффективности не представляет большой сложности; соответствующие методы изложены в специальных курсах. Однако это еще не решает основной задачи – выбора оптимального с точки зрения инвестора портфеля, отражающего его (инвестора) уровень толерантности к риску. Характеристикой степени толерантности (несклонности) инвесторов к риску служат так называемые кривые безразличия; при этом для каждого инвестора можно построить целое семейство таких кривых (рис 3.8). Очевидно, что с точки зрения конкретного инвестора оптимальным будет портфель, соответствующий точке касания одной из соответствующих кривых безразличия с границей эффективности.
Необходимо отметить, что приведенные выше рассуждения отнюдь не означают, что инвестор, формируя инвестиционный портфель, выполняет все описанные процедуры. Скорее наоборот, эти процедуры моделируют поведение инвестора, делая возможным управление инвестиционными процессами.
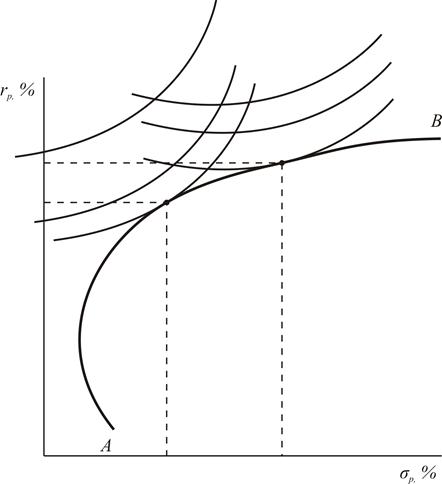
 Рис. 3.8. Выбор оптимального портфеля из набора эффективных.
Рис. 3.8. Выбор оптимального портфеля из набора эффективных.
Приложение 1. Вычисление коэффициента β
Расчет β- коэффициента по фактическим (историческим) данным сводится к построению так называемой характеристической линии, часто называемой также линией регрессии (графиком регрессионной зависимости)[Бригхем, Гапенски]. Характеристическая линия представляет собой график зависимости между доходностью рыночного портфеля (то есть, суррогата, его заменяющего) и доходностью ценной бумаги, для которой рассчитывается коэффициент β. Для построения зависимости используются статистические методы. При этом сама характеристическая линия аппроксимируется прямой, тангенс угла наклона которой к горизонтальной оси и есть коэффициент β.
В качестве примера вычисления используем расчет по гипотетическим данным, приведенный в [Levy, Sarnat, с. 190]. Вычисления можно проводить как с использованием специального финансового калькулятора, так и при помощи электронных таблиц Excel (последнее является более предпочтительным, так как позволяет наглядно, в распечатанном виде представить результаты расчета).
В рассматриваемом гипотетическом примере представлены данные, показывающие доходность некоторой ценной бумаги ri и доходность рыночного портфеля rm за период с 1978 по 1987 год (см. таблицу). Если принять безрисковую процентную ставку rf постоянной в течение всего периода, уравнение регрессии может быть представлено в виде:
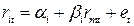 (3.15)
(3.15)
На основании этого уравнения и может быть рассчитан коэффициент β. В этом уравнении
rit – фактический доход на i-тую ценную бумагу в году t;
rmt – фактическая доходность рыночного портфеля в году t;
αi - точка пересечения характеристической линии i-той ценной бумаги с вертикальной осью;
βi - наклон характеристической линии, или мера системного риска;
et - случайная ошибка, отражающая различие между фактической доходностью i-той ценной бумаги в году t и доходностью, прогнозируемой при помощи характеристической линии.
Используя известные соотношения для определения βi, можно записать:
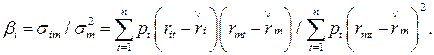 (3.16)
(3.16)
В рассматриваемом примере n = 10, а значения вероятностей pt равны единице, так как речь идет о фактической доходности. Результаты вычислений представлены в таблице 3.1.
В качестве упражнения рекомендуется приближенно построить характеристическую линию в прямоугольной декартовой системе координат. Для этого по горизонтальной оси необходимо отложить значения доходности рыночного портфеля по годам с 1978 по 1987, а по вертикальной оси – доход на i-тую ценную бумагу за те же периоды. Вычислив тангенс угла наклона построенной прямой к горизонтальной оси, следует сравнить его с исчисленным по формуле (3.16) значением βi.
Таблица 3.1. Вычисление коэффициента β.
| Год | ri | rm | ri – ři | rm – řm | (ri – ři)(rm – řm) | (rm – řm)2 |
| 5,20 | 7,40 | -17,83 | -12,40 | 221,09 | 153,76 | |
| 7,30 | 8,20 | -15,73 | -11,60 | 182,47 | 134,56 | |
| 10,10 | 12,30 | -12,93 | -7,50 | 96,98 | 56,25 | |
| 15,40 | 16,90 | -7,63 | -2,90 | 22,13 | 8,41 | |
| 19,80 | 19,10 | -3,23 | -0,70 | 2,26 | 0,49 | |
| 24,90 | 22,50 | 1,87 | 2,70 | 5,05 | 7,29 | |
| 29,70 | 25,10 | 6,67 | 5,30 | 35,35 | 28,09 | |
| 35,20 | 26,40 | 12,17 | 6,60 | 80,32 | 43,56 | |
| 40,10 | 29,80 | 17,07 | 10,00 | 170,70 | 100,00 | |
| 42,60 | 30,30 | 19,57 | 10,50 | 205,49 | 110,25 | |
| Итого: | 230,30 | 198,00 | 1021,83 | 642,66 | ||
| Среднее | 23,03 ři | 19,80 řm |
В соответствии с формулой (3.16) βi.= 1021.83/642.66 = 1.59.
Контрольные вопросы
1. Дайте определения следующих понятий: ожидаемый доход, дисперсия, стандартное отклонение, корреляция, диверсификация, системный и несистемный риск, β-коэффициент;
2. Охарактеризуйте понятие инвестиционного риска;
3. Приведите примеры несклонности инвесторов к риску из повседневной практики;
4. Поясните процесс оттока капиталов из России (притока капиталов в Россию) в терминах риска и ожидаемого дохода;
5. Приведите примеры ценных бумаг, представляющих различные компании либо отрасли, которые характеризуются а. позитивной корреляцией; б. негативной корреляцией; в. не коррелируют между собой;
6. Проанализируйте степень реалистичности допущений, лежащих в основе модели САРМ;
7. Каковы основные цели, преимущества и недостатки модели САРМ?
8. Охарактеризуйте линию рынка капитала и линию рынка ценной бумаги;
9. Что будут означать следующие значения коэффициента β для конкретной компании: β=1; β>1; β<1?
10. В чем, по Вашему мнению, заключаются причины сильной изменчивости коэффициентов β, рассчитываемых для российских предприятий?
| <== предыдущая страница | | | следующая страница ==> |
| Модель оценки капитальных активов (САРМ5) | | | Формирование бюджета (сметы) капитальных вложений |
Дата добавления: 2014-03-19; просмотров: 267; Нарушение авторских прав

Мы поможем в написании ваших работ!