Пересечение плоскостей синхронизации

Угловая засечка хорд

Пространственная угловая засечка

Идея космической триангуляции принадлежит финскому геодезисту И. Вяйсяля. Суть ее заключается в том, что при одновременных фотографических наблюдениях ИСЗ из разных пунктов земной поверхности по известным координатам некоторых из них, можно вычислить координаты ИСЗ и координаты определяемых пунктов.

1). Пространственная угловая засечка

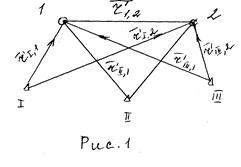
Два пункта, исходный, один определяемый.

Необходимо наблюдать спутник в 2х

положениях или наблюдать 2 разных ИСЗ.

Недостаток:

синхронность наблюдений с трех пунктов.

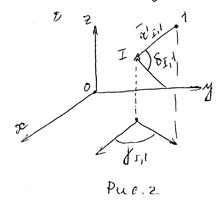
Согласно рис.2 по каждому направлению имеем:

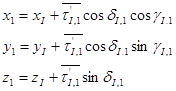(5)

Если определить x, y,z по наблюдениям со второго пункта, то:

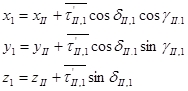(6)

Так как левые части равенств (5) и (6) равны, то прировняв правые, получим систему из 3х уравнений, в которых 2 неизвестных 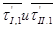, которые найдем в этом случае с контролем.

Необходимым условием реализации рассмотренного построения является фиксирование моментов каждого наблюдения ИСЗ. Основной трудностью практического осуществления данного построения состоит в обеспечении одновременной видимости спутника с трех станций, удаленных на значительные расстояния. Более гибким в этом отношении является метод хорд.

2.) Угловая засечка хорд.

Достаточно выполнить наблюдения двух положений спутника одновременно с определяемого и одного из исходных пунктов.

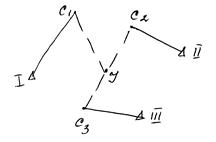
В этом методе получим хорду, как линию, образованную от пересечения плоскостей синхронизации. Например, на рис плоскость синхронизации IC₂ A пересекаются, образуя хорду IA, для которой ориентирующие углы λ_I,A Ф_I,A , необходимо определить.

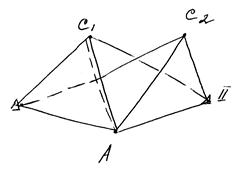
Для этого выполняются 2 пары синхронных наблюдений с I и A, а затем со II и А. Фактически, наблюдения необходимо выполнить с трех пунктов, но обеспечить одновременную синхронизацию наблюдений только с двух пунктов. Тогда:

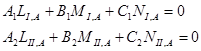(7)

Где

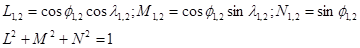
С учетом этого и полагая, что N≠0 , получим:

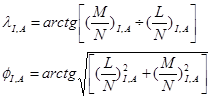
По аналогичным формулам находят λ_II,A Ф_II,A. Затем по формулам пространственной угловой засечки вычисляют координаты искомого пункта.

3.) Пересечение плоскостей синхронизации

Очень часто возникает ситуация, когда:

В зависимости от удаленности пунктов

наблюдений друг от друга; в зависимости

от характера траектории ИСЗ; в зависимости

от условий видимости спутников и от

ряда других причин может оказаться, что каждое положение спутника можно наблюдать только с двух пунктов, определяемого и исходного. Для такого случая, уравнения трех плоскостей синхронизации будут иметь вид:

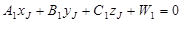где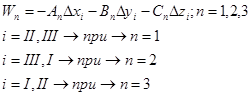

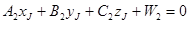
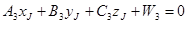
Комбинированные построения.

Дата добавления: 2014-03-24; просмотров: 508; Нарушение авторских прав

Мы поможем в написании ваших работ!