Понятия об искажениях длин, площадей и углов

Картографическим искажением называют нарушение геометрических свойств участков земной поверхности и расположенных на них объектов при изображении их на плоскости.

Имеется 4-ре вида картографических искажений: длин линий, углов, формы, площади. Эти искажения зависят от свойств проекции. Длины линий искажаются во всех проекциях, кроме отдельных линий и точек на картах.

Искажение длин линий – связано с изменением масштаба длин на одной и той же карте и выражается в том, что расстояния одинаковые на уровенной поверхности Земли изображаются на этой карте отрезками разной длины. Каждая карта имеет главный масштаб 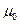, который показывает общую степень уменьшения всей картографируемой поверхности при ее изображении на плоскости.

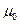- не влияет на свойство проекции, и его принимают = 1.

Частным масштабом длин 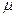- называется отношение бесконечно малого отрезка в проекции к соответствующему бесконечно-малому отрезку на картографируемой поверхности: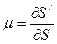. (1.8)

Частный масштаб является функцией географических координат и азимута направления: 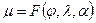, он определяет свойство проекций. (1.9)

Принято частные масштабы по координатным линиям называть масштабами по меридианам и параллелям:

По меридианам - 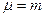, при a=0 или 180⁰.

По параллелям - 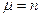, при a=90 или 270⁰.

Искажением длин называется разность между частным масштабом длин и единицей, выраженная в %: 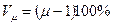. . 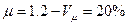Частные масштабы длин отрицательными быть не могут, если 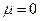, то изображение пропадает.

Частным масштабом площади (Р) называется отношение бесконечно малого участка на карте к соответствующему участку на картографируемой поверхности: 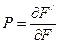(1.10)

Обычно 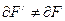, но имеется отдельный случай, когда 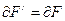, тогда проекции называются равновеликие.

Частный масштаб площади зависит только от географических координат.

Искажением площади называется разность между масштабом площади и 1, выраженный в %: 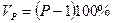(1.11)

Искажения углов (DU) – характеризуются разностью между величиной угла проекции и величиной соответствующего угла на картографируемой поверхности.

Общая теория картографических проекций

1. Вывод общей формулы частного масштаба длин.

Масштабы по меридианам и параллелям.

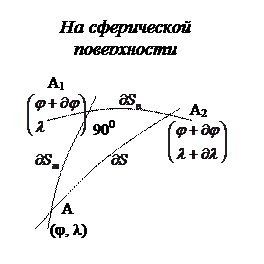
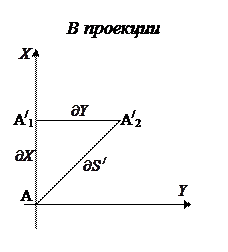
Рассмотрим элементарные треугольники и выразим элементарные отрезки: .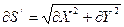

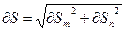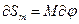- дуга меридианов;

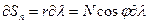- дуга параллели.

r – радиус параллели

M – радиус меридиана

N – радиус 1-го вертикала.

Частный масштаб определится формулой: 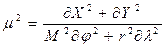, после преобразований формула примет окончательный вид:

,

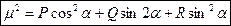где ; ;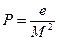

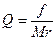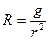
коэффициенты Гаусса:

; ;

; .

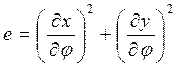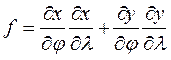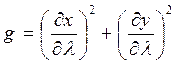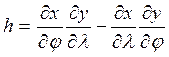Масштаб по меридианам (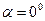или 180⁰) - 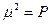, обозначим ,

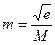Масштаб по параллелям (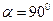или 270⁰) - 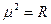, обозначим ,

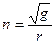2. Масштаб площади

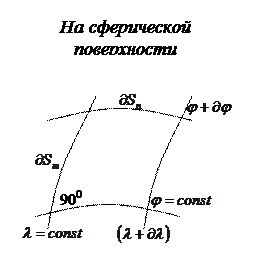
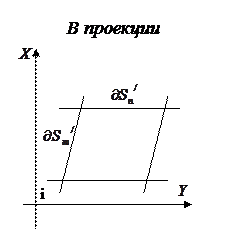
Масштаб площади определится по формуле: ,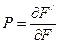

где 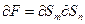и 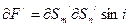, следовательно .

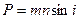По положениям Апполония: 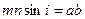, тогда .

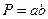Если учесть показатель неортогональности 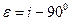, то масштаб площади будет следующим .

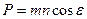При 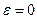(i=90⁰) 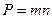, подставим в формулу значения масштабов по меридианам и параллелям, окончательно будем иметь: .

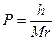3. Изображение азимута в проекции

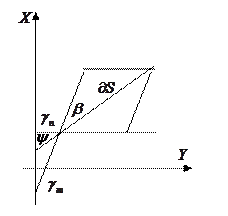
Азимут произвольного направления a в проекции обозначается b. Согласно рисунку.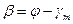

Угол y образует элементарный отрезок 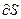с положительным направлением оси X, по аналогии углы 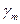и 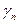образуются при пересечении меридиана и параллели с положительным направлением оси X.

Найдем значения этих углов:

, , .

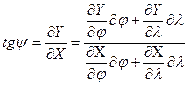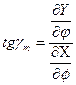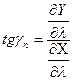Используя выражения тангенсов и выполняя определенные преобразования можно написать формулы устанавливающие свяхзь между азимутом на поверхности эллипсоида и соответствующим ему углом на плоскости:

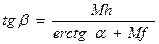или .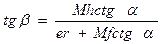

4. Угол между меридианами и параллелями

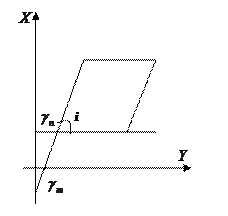
Рассмотрим данный рисунок: .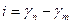

Вычислим тангенс угла и выразим полученное выражение через коэффициенты Гаусса: 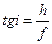, учитывая, что 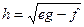, формулу можно записать:

или .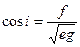

5. Условия ортогональности картографической сетки

Полученные формулы позволяют определить четверть, в которой находится угол i,

если 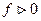, то это I четверть

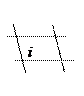
если 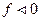, то это II четверть

если 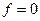, то сетка ортогональна

Условие ортогональности имеет вид:

.

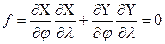, сетка будет ортогональна, когда 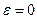, а это возможно если числитель .

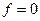Основы составления топокарт

Дата добавления: 2014-03-24; просмотров: 876; Нарушение авторских прав

Мы поможем в написании ваших работ!