Закономерности движения для стока воздуха в узкую щель

Рассмотрим сток для узкой щели (рис. VII.3).

Рис. VII.3. Сток воздуха в узкую щель.

Через длинную щель шириной 2В_о удаляется воздух в количестве L_о со скоростью . Определим компоненту скорости вдоль оси Х в произвольной точке пространства перед щелью. Считаем, что линии тока образующегося течения направлены по кратчайшему пути к всасывающей щели. Разделим всасывающую щель на бесконечно тонкие полоски длиной, равной длине щели, и шириной db. Одна из таких полосок находится на расстоянии «в» от начала координат, которое совпадает с центром щели. Через элемент щели площадью dbl_о будет отсасываться элементарный объем воздуха dL = dbl_o, который вызовет элементарную скорость воздуха 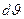в точках пространства. Поле равных скоростей будет представлять собой половину боковой поверхности цилиндра радиуса R, и, следовательно, будет справедливо равенство

. (15.6)

Так как элементарный расход dL может быть представлен через общий расход воздуха в щели , то элементарная скорость 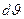запишется в виде

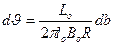. (15.7)

Компонента скорости в направлении оси Х

. (15.8)

Поскольку расстояние от рассматриваемой точки до элементарной полосы 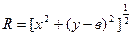, зависимость (21.8) примет вид

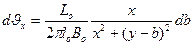. (15.9)

После интегрирования по в в пределах от -В_о до +В_о компонента скорости потока, стекающего к щели шириной 2В_о, составит

. (15.10)

Имея в виду, что , формулу (21.10) перепишем в виде:

; (15.11)

на оси потока у = 0, и осевая скорость окажется равной

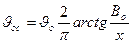. (15.12)

Спектр скоростей всасывания для отверстия квадратной формы мало отличается от спектра для круглого отверстия. Так, если для круглого отверстия _ост / _о.ц. = 0,05, оказывается на расстоянии х » 1,03d_о, то для квадратного отверстия – на расстоянии 1,2 × 2В_о.

Зона всасывания у вытяжных отверстий прямоугольной формы оказывается более активной, чем у круглых или квадратных отверстий, так как такие отверстия по форме приближаются к линейному стоку и тем больше, чем больше соотношение их сторон.

Лекция № 16 Расчет воздуховодов

План

Дата добавления: 2014-04-10; просмотров: 380; Нарушение авторских прав

Мы поможем в написании ваших работ!