ММ-8. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТИЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ КВАДРАТНОЙ МАТРИЦЫ

7.1. Что называется ограниченным носителем?

А. Элементом наилучшего приближения элемента 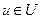в подпространстве 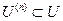называется линейная комбинация координатных функций..

Б. Элементом наилучшего приближения элемента 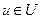в подпространстве 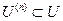называется работа внутренних сил на возможных перемещениях.

В. Элементом наилучшего приближения элемента 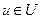в подпространстве 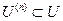называется работа внутренних сил на действительных перемещениях.

Г. Элементом наилучшего приближения элемента 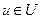в подпространстве 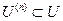называется такой элемент 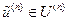, для которого выполняется требование .

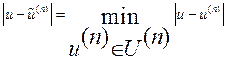6.2. Что называется координатными функциями?

А. Заранее выбранные в (для метода Ритца) и в (для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

Б. Заранее выбранные в 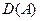(для метода Ритца) и в 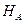(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

В. Разность между левой и правой частями дифференциального уравнения задачи.

Г. Правая часть дифференциального уравнения задачи.

6.3. Что называется координатной системой?

А. Система коэффициентов линейной аппроксимации решения.

Б. Система коэффициентов линейной аппроксимации свободного члена дифференциального уравнения задачи.

В. Система координатных функций 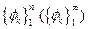, удовлетворяющая определённым требованиям, обеспечивающим сходимость последовательности приближённых решений и повышающих устойчивость процесса счёта.

Г. Система ортов осей координат.

6.4. В чём заключается метод Ритца?

А. В использовании линейной аппроксимации решения.

Б. В следующих действиях

1) формулируется вариационная задача, эквивалентная данной краевой задаче;

2.) выбирается координатная система, отвечающая установленным требованиям;

3) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) определяются коэффициенты Ритца;

б) определяются свободные члены системы уравнений Ритца;

в) решается система уравнений Ритца;

г) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

д) принимается решение о продолжении счёта или выходе из цикла;

4) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта и вычисляются значения исокмой функции в назаначенных точках её области определения.

В. В использовании линейной апроксимации свободного члена дифференциального уравнения задачи.

Г. В сведении краевой задачи к вариационной.

6.5. В чём заключается метод Бубнова-Галёркина?

А. В использовании линейной аппроксимации решения

Б. В следующем

1) формулируется вариационная задача, эквивалентная данной краевой задаче;

2.) выбирается координатная система, отвечающая установленным требованиям;

3) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) определяются коэффициенты Ритца;

б) определяются свободные члены системы уравнений Ритца;

в) решается система уравнений Ритца;

г) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

д) принимается решение о продолжении счёта или выходе из цикла;

4) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта и вычисляются значения исокмой функции в назаначенных точках её области определения.

В. В использовании линейной апроксимации свободного члена дифференциального уравнения задачи.

Г. В следующем

1) выбирается координатная система, отвечающая установленным требованиям;

2) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) записываются условия ортогональности невязки функциям координатной подсистемы;

б) определяются коэффициенты системы линейных алгебраических уравнений метода;

в) определяются свободные члены этой системы;

г) решается эта система уравнений;

д) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

е) принимается решение о продолжении счёта или выходе из цикла;

3) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта;

4) вычисляются значения исокмой функции в назаначенных точках её области определения.

.

6.1. «Г» - Элементом наилучшего приближения элемента 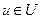в подпространстве 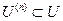называется такой элемент 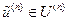, для которого выполняется требование .

6.2. «А» - Заранее выбранные в 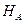(для метода Ритца) и в 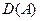(для метода Бубнова-Галёркина) функции, при помощи линейной комбинации которых записывается приближённое решение.

6.3. «В» - Система координатных функций 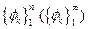, удовлетворяющая определённым требованиям, обеспечивающим сходимость последовательности приближённых решений и повышающих устойчивость процесса счёта.

6.4. «Б» - В следующем

1) формулируется вариационная задача, эквивалентная данной краевой задаче;

2.) выбирается координатная система, отвечающая установленным требованиям;

3) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) определяются коэффициенты Ритца;

б) определяются свободные члены системы уравнений Ритца;

в) решается система уравнений Ритца;

г) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

д) принимается решение о продолжении счёта или выходе из цикла;

4) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта и вычисляются значения исокмой функции в назаначенных точках её области определения.

6.5. «Г» - В следующем

1) выбирается координатная система, отвечающая установленным требованиям;

2) поочерёдно выбираются координатные подсистемы с растущим количеством координатных функций в них и для каждой подсистемы

а) записываются условия ортогональности невязки функциям координатной подсистемы;

б) определяются коэффициенты системы линейных алгебраических уравнений метода;

в) определяются свободные члены этой системы;

г) решается эта система уравнений;

д) сравнивается норма разности решений с допускаемой величиной (можно сравнивать два последовательных набора коэффициентов, исключая последний коэффициент последующего набора);

е) принимается решение о продолжении счёта или выходе из цикла;

3) формируется линейная комбинация координатных функций с полученными коэффициентами последнего расчёта;

4) вычисляются значения исокмой функции в назаначенных точках её области определения.

ММ-8. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТИЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ КВАДРАТНОЙ МАТРИЦЫ

Ключевые слова и понятия

8.1. Собственно значение матрицы.

8.2. Собственный вектор матрицы.

8.3. Метод обратных итераций.

8.4. Степенной метод.

8.5. Метод сдвига.

Дата добавления: 2014-04-15; просмотров: 352; Нарушение авторских прав

Мы поможем в написании ваших работ!