
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Входная информация для самопроверки
Для изучения данной темы Вам необходимо восстановить в памяти:
- из курса прикладной математики – решение систем линейных однородных и неоднородных алгебраических уравнений,понятия линейной и векторной алгебры, собственные значения и собственные вектора квадратной матрицы, системы линейно независимых векторов;
-из настоящего спецкурса - понятия: линейного пространства, подпространства и нормированного пространства.
8.2. Содержание темы.
 8.2.1. Структурно – логическая схема содержания темы
8.2.1. Структурно – логическая схема содержания темы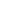
 |

 8.2.2. Тематическое содержание.
8.2.2. Тематическое содержание.
Напомним некоторые сведения из курса линейной алгебры.
Если А — квадратная матрица п-гопорядка и 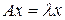 при
при 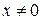 , то число
, то число 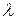 называется собственным, значением матрицы, а ненулевой вектор х — соответствующим ему собственным вектором. Перепишем задачу в виде
называется собственным, значением матрицы, а ненулевой вектор х — соответствующим ему собственным вектором. Перепишем задачу в виде
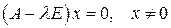 (8.1.)
(8.1.)
Для существования нетривиального решения задачи (8.1) должно выполняться условие
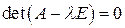 (8.2)
(8.2)
Этот определитель является многочленом 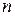 -й степени относительно
-й степени относительно 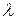 ; его называют характеристическим многочленом. Значит, существует п собственных значений — корней этого многочлена, среди которых могут быть одинаковые (кратные). В принципе можно вычислить характеристический многочлен и найти все его корни.
; его называют характеристическим многочленом. Значит, существует п собственных значений — корней этого многочлена, среди которых могут быть одинаковые (кратные). В принципе можно вычислить характеристический многочлен и найти все его корни.
Если найдено некоторое собственное значение, то, подставляя его в однородную систему (8.1), можно определить соответствующий собственный вектор. Будем нормировать собственные векторы. Тогда каждому простому (не кратному) собственному значению соответствует один (с точностью до направления) собственный вектор, а совокупность всех собственных векторов, соответствующих совокупности простых собственных значений, линейно – независима. Таким образом, если все собственные значения матрицы простые, то она имеет п линейно-независимых собственных векторов, которые образуют базис пространства .
Пример.
Заданы осевые и центробежные моменты инерции некоторого пространственного тела в центральных осях: 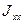 =6 кн
=6 кн 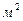 ,
, 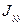 =5 кн
=5 кн 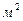 ,
,  =7 кн
=7 кн 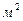 ,
, 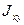 =-2 кн
=-2 кн 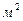 ,
, 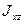 =2 кн
=2 кн 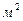 ,
, 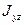 =0. Найти значения главных центральных моментов инерции и их направления.
=0. Найти значения главных центральных моментов инерции и их направления.
Решение.
Составим матрицу центральных моментов инерции
A=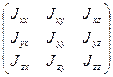 =
=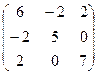 .
.
Запишем характеристическое уравнение (8.2) и найдем собственные значения этой матрицы:
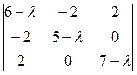 =0.
=0.
Раскрывая определитель , получим:
(6-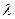 )(5-
)(5-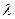 )(7-
)(7-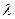 ) – 4(5-
) – 4(5-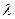 )-4(7-
)-4(7-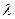 )=0,
)=0,
(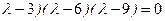 .
.
Отсюда находим собственные значения матрицы: 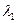 =3,
=3, 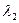 =6,
=6, 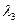 =9.
=9.
Найдем собственный вектор 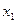 , соответствующий первому собственному значению
, соответствующий первому собственному значению 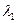 =3 из уравнения (8.1)
=3 из уравнения (8.1)

(A-3E)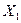 =0.
=0.
Запишем это уравнение в координатной форме
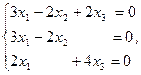
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
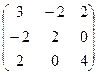
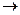
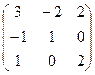
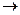

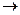
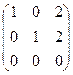
Таким образом, система имеет решение: 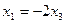 ,
, 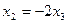 , а собственный вектор
, а собственный вектор 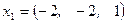 .
.
Найдем собственный вектор 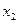 , соответствующий второму собственному значению
, соответствующий второму собственному значению 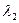 =6 из уравнения (8.1)
=6 из уравнения (8.1)

(A-6E)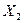 =0.
=0.
Запишем это уравнение в координатной форме
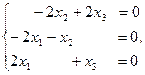
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
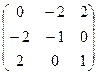
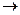
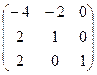
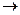
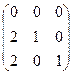 .
.
Таким образом, система имеет решение: 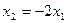 ,
, 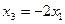 , а собственный вектор
, а собственный вектор 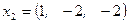 .
.
Найдем собственный вектор 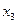 , соответствующий второму собственному значению
, соответствующий второму собственному значению 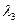 =9 из уравнения (8.1)
=9 из уравнения (8.1)

(A-9E)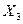 =0.
=0.
Запишем это уравнение в координатной форме
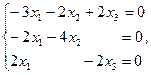
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
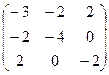
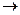
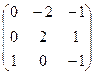 .
.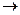
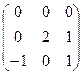 .
.
Таким образом, система имеет решение: 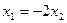 ,
, 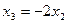 , а собственный вектор
, а собственный вектор 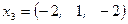 .
.
Однако, если степень многочлена достаточно высокая, то аналитически определить корни достаточно сложно. И в этом случае их определяют численными методами.
Если собственное значение известно, то собственный вектор .удовлетворяет системе (8.1). Но любой численный метод дает вместо точного собственного значения 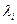 приближенное значение
приближенное значение 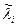
 , так что
, так что 
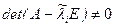 , хотя отличается от нуля очень мало. В таком случае задача
, хотя отличается от нуля очень мало. В таком случае задача 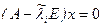 при использовании приближенного собственного значения имеет только тривиальное решение x=0. Поэтому при численных расчетах находить собственные векторы непосредственно из системы (8.1) нельзя.
при использовании приближенного собственного значения имеет только тривиальное решение x=0. Поэтому при численных расчетах находить собственные векторы непосредственно из системы (8.1) нельзя.
- Метод обратных интеграций.
Для нахождения собственных векторов удобен метод обратной итерации, заключающийся в следующем. Выберем наудачу вектор b и рассмотрим линейную неоднородную систему
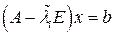 (8.3)
(8.3)
Определитель этой системы отличен от нуля, так что она имеет единственное решение. Покажем, что найденный из нее вектор x окажется почти равным собственному вектору 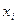 соответствующему данному собственному значению
соответствующему данному собственному значению 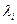 .
.
Для простоты ограничимся случаем, когда матрица n-го порядка имеет n линейно-независимых собственных векторов 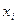 — например, матрица нормальная (случай произвольных матриц рассмотрен ниже). Тогда собственные векторы образуют базис, по которому можно разложить векторы x и b:
— например, матрица нормальная (случай произвольных матриц рассмотрен ниже). Тогда собственные векторы образуют базис, по которому можно разложить векторы x и b:
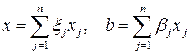 (8.4)
(8.4)
Подставляя это разложение в систему (8.3), перенося все члены влево и учитывая, что 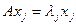 , получим
, получим
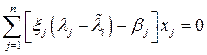 (8.5)
(8.5)
Поскольку собственные векторы линейно – независимы, то их линейная комбинация обращается в нуль только в том случае, когда все ее коэффициенты равны нулю. Поэтому из (8.5) следует
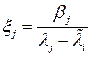 (8.6)
(8.6)
Видно, что если 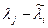 - мало, то коэффициент
- мало, то коэффициент 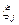 будет очень большим; в противном случае он невелик. Рассмотрим следствия из этого в трех основных случаях.
будет очень большим; в противном случае он невелик. Рассмотрим следствия из этого в трех основных случаях.
Первый случай — собственное значение 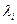
 простое. Тогда из всех коэффициентов
простое. Тогда из всех коэффициентов 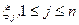 , , только один коэффициент
, , только один коэффициент 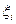 оказывается очень большим. Это означает, что найденный вектор x почти совпадает с собственным вектором
оказывается очень большим. Это означает, что найденный вектор x почти совпадает с собственным вектором 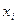 (с точностью до нормировочного множителя), что и требовалось доказать. Заметим, что поскольку найденный вектор
(с точностью до нормировочного множителя), что и требовалось доказать. Заметим, что поскольку найденный вектор 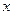 оказывается очень большим, то его обычно нормируют.
оказывается очень большим, то его обычно нормируют.
Из (8.6) видно, что при обратной итерации (т. е. при переходе от b к x) компонента 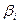 усиливается по сравнению с другими компонентами примерно во столько раз, во сколько погрешность данного собственного значения меньше разности соседних собственных значений. Поэтому чем точнее найдено
усиливается по сравнению с другими компонентами примерно во столько раз, во сколько погрешность данного собственного значения меньше разности соседних собственных значений. Поэтому чем точнее найдено 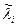 (очевидно, хорошая точность особенно важна при наличии близких собственных значений), тем ближе x будет к
(очевидно, хорошая точность особенно важна при наличии близких собственных значений), тем ближе x будет к 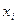 . Если собственные значения найдены слишком грубо, или случайно вектор
. Если собственные значения найдены слишком грубо, или случайно вектор 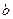 выбран неудачно, так что
выбран неудачно, так что 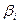 - очень мало, то разница между x и
- очень мало, то разница между x и 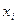 может оказаться заметной. Тогда подставляют найденный вектор x в правую часть уравнения (8.3) вместо b и организуют итерационный процесс
может оказаться заметной. Тогда подставляют найденный вектор x в правую часть уравнения (8.3) вместо b и организуют итерационный процесс
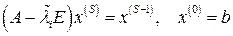 (8.7)
(8.7)
Обычно он сходится настолько быстро, что двух итераций вполне достаточно. Напомним, что на каждой итерации обязательно надо нормировать найденные 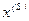 чтобы не получать в расчетах слишком больших чисел, вызывающих переполнение на ЭВМ.
чтобы не получать в расчетах слишком больших чисел, вызывающих переполнение на ЭВМ.
Замечание 8.1. Очень эффективен один простой способ выбора b. В качестве его компонент в декартовых координатах возьмем последовательные многоразрядные псевдослучайные числа 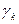 . Тогда вероятность того, что
. Тогда вероятность того, что 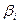 окажется очень малым, будет ничтожна.
окажется очень малым, будет ничтожна.
Второй случаи — собственное значение 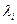 кратно; например,
кратно; например, 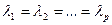 ,
,  . Напомним, что в этом случае собственные векторы
. Напомним, что в этом случае собственные векторы 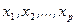 определены неоднозначно; любая их линейная комбинация удовлетворяет уравнению
определены неоднозначно; любая их линейная комбинация удовлетворяет уравнению
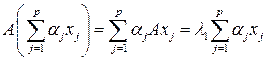
и являются собственным вектором. Т.е. они порождают p – мерное подпространство, любой базис которого можно взять в качестве системы искомых собственных векторов.
Теперь из (8.6) следует, что большими оказываются коэффициенты 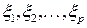 , причем степень их усиления одинакова; остальные коэффициенты остаются малыми. Значит, найденный из (8.3) вектор х будет приближенно линейной комбинацией
, причем степень их усиления одинакова; остальные коэффициенты остаются малыми. Значит, найденный из (8.3) вектор х будет приближенно линейной комбинацией 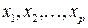 , а тем самым — искомым собственным вектором. Если точность полученного приближения недостаточна, то обратную итерацию повторяют снова по формуле (8.7).
, а тем самым — искомым собственным вектором. Если точность полученного приближения недостаточна, то обратную итерацию повторяют снова по формуле (8.7).
Чтобы найти все собственные векторы для кратного собственного значения, возьмем столько линейно-независимых векторов 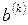 ,какова кратность корня. Обратными итерациями получим столько же векторов
,какова кратность корня. Обратными итерациями получим столько же векторов 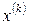 , которые и будут искомыми; они будут линейно-независимыми, поскольку преобразование (8.3) невырожденное. Остается только ортогонализовать найденные векторы, если это требуется по условиям задачи.
, которые и будут искомыми; они будут линейно-независимыми, поскольку преобразование (8.3) невырожденное. Остается только ортогонализовать найденные векторы, если это требуется по условиям задачи.
Напомним, что в качестве декартовых координат векторов 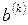 целесообразно брать псевдослучайные числа; здесь это имеет то дополнительное преимущество, что векторы автоматически получаются линейно-независимыми.
целесообразно брать псевдослучайные числа; здесь это имеет то дополнительное преимущество, что векторы автоматически получаются линейно-независимыми.
Третий случай — когда матрица имеет кратные корни, но число ее собственных векторов меньше п — выходит за рамки нашего доказательства. Однако метод обратных итераций здесь также применим в той форме, которая описана для кратных корней. Разница лишь в том, что если 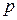 -кратному собственному значению соответствуют всего
-кратному собственному значению соответствуют всего 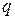 собственных векторов
собственных векторов 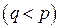 , то из полученных обратной итерацией векторов
, то из полученных обратной итерацией векторов 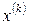 только
только 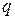 будут линейно-независимыми. Это выясняется при их ортогонализации: первые
будут линейно-независимыми. Это выясняется при их ортогонализации: первые 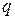 векторов ортогонализуются «без приключений», а при ортогонализации следующих векторов их компоненты обращаются почти в нуль (в пределах погрешности расчета).
векторов ортогонализуются «без приключений», а при ортогонализации следующих векторов их компоненты обращаются почти в нуль (в пределах погрешности расчета).
Каков объем расчетов в методе обратной итерации? Нахождение собственного вектора требует (при одной итерации) не более 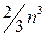 действий, так что для нахождения всех их надо около
действий, так что для нахождения всех их надо около 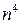 арифметических действий. Таким образом, при больших порядках матрицы метод неэкономичен, но при
арифметических действий. Таким образом, при больших порядках матрицы метод неэкономичен, но при 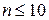 вполне удовлетворителен. Особенно употребителен этот метод из-за своей простоты, универсальности и хорошей устойчивости алгоритма.
вполне удовлетворителен. Особенно употребителен этот метод из-за своей простоты, универсальности и хорошей устойчивости алгоритма.
В некоторых частных случаях расчеты существенно упрощаются и ускоряются. Наиболее важен случай трехдиагональной матрицы. При этом линейная система уравнений (8.3) для определения компонент собственных векторов также будет трехдиагональной, и ее решают экономичным методом прогонки по несложным формулам. Для вычисления одного собственного вектора в этом случае требуется 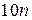 , а для всех—
, а для всех—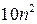 арифметических действий.
арифметических действий.
Для почти треугольной матрицы в методе обратных итераций требуется решать линейную систему с почти треугольной матрицей, что делается специальным вариантом метода исключения. Если учесть, что случайный вектор в правой части (8.3) можно задавать уже после приведения матрицы в методе исключения Гаусса к треугольной форме, то нахождение каждого собственного вектора требует 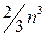 действий (тот же прием для трехдиагональной матрицы позволяет сократить число действий до
действий (тот же прием для трехдиагональной матрицы позволяет сократить число действий до 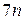 ).А для нахождения всех собственных векторов требуется соответственно
).А для нахождения всех собственных векторов требуется соответственно 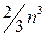 арифметических действий.
арифметических действий.
Отметим одну существенную деталь. Поскольку 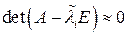 , то при нахождении собственных векторов в формулах прямого хода метода исключений (прогонки) на главной диагонали появится хотя бы один очень малый элемент. Чтобы формально можно было вести расчет, диагональные элементы не должны обращаться в нуль; для этого надо, чтобы погрешность собственного значения была не слишком мала, т. е. составляла бы 10—15 последних двоичных разрядов числа на ЭВМ. Если корни характеристического многочлена находят методом парабол (или секущих), то такая погрешность получается естественно, ибо из-за ошибок округления эти методы перестают сходиться в очень малой окрестности корня. Но если корни определялись методом Ньютона, то при этом могли быть найдены верно все знаки собственного значения; тогда, чтобы избежать деления на нуль, приходится специально вносить в
, то при нахождении собственных векторов в формулах прямого хода метода исключений (прогонки) на главной диагонали появится хотя бы один очень малый элемент. Чтобы формально можно было вести расчет, диагональные элементы не должны обращаться в нуль; для этого надо, чтобы погрешность собственного значения была не слишком мала, т. е. составляла бы 10—15 последних двоичных разрядов числа на ЭВМ. Если корни характеристического многочлена находят методом парабол (или секущих), то такая погрешность получается естественно, ибо из-за ошибок округления эти методы перестают сходиться в очень малой окрестности корня. Но если корни определялись методом Ньютона, то при этом могли быть найдены верно все знаки собственного значения; тогда, чтобы избежать деления на нуль, приходится специально вносить в 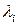 небольшие погрешности.
небольшие погрешности.
- Степенной метод .
Степенной метод (счет на установление) применяется для получения наибольшего по модулю собственного значения. Пусть 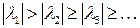 . Построим такой итерационный процесс:
. Построим такой итерационный процесс:
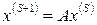 (8.8)
(8.8)
Он не сходится в обычном смысле. Разложим нулевое приближение по собственным векторам матрицы: 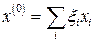 . Тогда легко убедиться, что
. Тогда легко убедиться, что 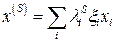 и при достаточно большом числе итераций
и при достаточно большом числе итераций 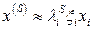 ,т. е. вектор
,т. е. вектор  сходится к собственному вектору по направлению. Очевидно, при этом
сходится к собственному вектору по направлению. Очевидно, при этом 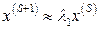 .
.
Процесс сходится линейно со знаменателем 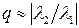 . Считается, что процесс практически сошелся, если отношения соответствующих координат векторов
. Считается, что процесс практически сошелся, если отношения соответствующих координат векторов 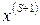 и
и  с требуемой точностью одинаковы и не меняются на последних итерациях. При этом для более точного получения собственного значения целесообразно положить
с требуемой точностью одинаковы и не меняются на последних итерациях. При этом для более точного получения собственного значения целесообразно положить
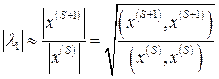 (8.9)
(8.9)
Отметим, что при расчетах на ЭВМ на каждой итерации после вычисления 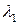 вектор
вектор 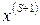 надо нормировать, чтобы не получать переполнений или исчезновений чисел.
надо нормировать, чтобы не получать переполнений или исчезновений чисел.
Формально при 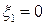 итерации сходятся к следующему собственному значению. Однако из-за ошибок округления
итерации сходятся к следующему собственному значению. Однако из-за ошибок округления 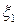 не может быть точно нулем, а при малом
не может быть точно нулем, а при малом 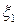 процесс по-прежнему сходится к первому собственному значению, только за большее число итераций.
процесс по-прежнему сходится к первому собственному значению, только за большее число итераций.
Если наибольшее собственное значение кратное, но соответствующий элементарный делитель матрицы линеен, то итерации сходятся обычным образом. Но если 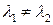 , а их модули равны или если элементарный делитель матрицы нелинеен (жорданова клетка), то процесс не сходится.
, а их модули равны или если элементарный делитель матрицы нелинеен (жорданова клетка), то процесс не сходится.
Если  , то сходимость очень медленная; этот случай нередко встречается в простейших итерационных методах решения разностных схем для эллиптических уравнений. Тогда сходимость можно ускорить процессом Эйткена.
, то сходимость очень медленная; этот случай нередко встречается в простейших итерационных методах решения разностных схем для эллиптических уравнений. Тогда сходимость можно ускорить процессом Эйткена.
Одна итерация для матрицы общего вида требует 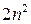 арифметических действий, а для ленточной матрицы — 2тп действий. Из-за медленной сходимости степенной метод применяют только к матрицам, содержащим очень много нулевых элементов (и даже к ним— довольно редко).
арифметических действий, а для ленточной матрицы — 2тп действий. Из-за медленной сходимости степенной метод применяют только к матрицам, содержащим очень много нулевых элементов (и даже к ним— довольно редко).
В математической литературе описана вариация степенного метода, имеющая квадратичную сходимость: 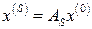 , где
, где 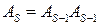 и
и 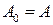 . Однако если матрица А имеет много нулевых элементов, то ее степени уже такими не будут. Поэтому этот вариант обычно не экономичен.
. Однако если матрица А имеет много нулевых элементов, то ее степени уже такими не будут. Поэтому этот вариант обычно не экономичен.
- Обратные итерации со сдвигом.
Напишем итерационный процесс, обратный по отношению к степенному процессу:
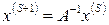 (8.10)
(8.10)
Очевидно, он сходится в указанном в предыдущем пункте смысле к наибольшему по модулю собственному значению матрицы 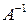 , т. е. к наименьшему по модулю собственному значению матрицы А (ибо собственные значения матриц А и
, т. е. к наименьшему по модулю собственному значению матрицы А (ибо собственные значения матриц А и 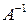 обратные друг другу). Все, что говорилось в предыдущем пункте о характере сходимости, разумеется, справедливо и в этом случае; сходимость будет довольно медленной.
обратные друг другу). Все, что говорилось в предыдущем пункте о характере сходимости, разумеется, справедливо и в этом случае; сходимость будет довольно медленной.
Однако здесь положение можно существенно улучшить методом сдвига, который заключается в следующем. Пусть нам приближенно известно некоторое, не обязательно наименьшее, собственное значение 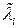 Тогда так называемая сдвинутая матрица
Тогда так называемая сдвинутая матрица 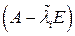 будет иметь собственные значения
будет иметь собственные значения 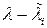 . У этой матрицы интересующее нас собственное значение
. У этой матрицы интересующее нас собственное значение 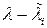 будет намного меньше по модулю, чем остальные. Поэтому обратные итерации со сдвинутой матрицей (которые мы запишем в несколько иной форме)
будет намного меньше по модулю, чем остальные. Поэтому обратные итерации со сдвинутой матрицей (которые мы запишем в несколько иной форме)
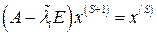 , (8.11)
, (8.11)
будут быстро сходиться и определят требуемое нам собственное значение 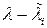 . Напомним, что после каждой итерации надо нормировать вектор, чтобы избежать переполнений. С учетом этого вместо (8.11) получим последовательность формул
. Напомним, что после каждой итерации надо нормировать вектор, чтобы избежать переполнений. С учетом этого вместо (8.11) получим последовательность формул
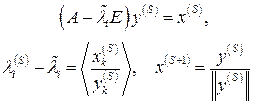 (8.12)
(8.12)
Здесь индекс 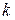 относится к компонентам векторов, а скобки
относится к компонентам векторов, а скобки 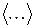 означают некоторое усреднение по всем компонентам: например, среднеарифметическое.
означают некоторое усреднение по всем компонентам: например, среднеарифметическое.
Если исходное приближение было хорошим, то иногда процесс сходится за несколько итераций; тогда выгодно непосредственно решать линейную систему (8.10). Если же требуемое число итераций велико, то лучше обратить матрицу 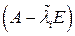 . Выгодней всего при решении линейной системы (8.11) методом исключения Гаусса использовать полученные на первой же итерации вспомогательные коэффициенты
. Выгодней всего при решении линейной системы (8.11) методом исключения Гаусса использовать полученные на первой же итерации вспомогательные коэффициенты 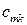 на каждой последующей итерации; но это не предусмотрено в обычных стандартных программах.
на каждой последующей итерации; но это не предусмотрено в обычных стандартных программах.
Если сдвиг постоянный, то итерации сходятся линейно. Можно получить квадратичную сходимость, если уточнять сдвиг в ходе расчета следующим образом
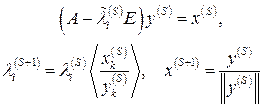 (8.13)
(8.13)
Для матриц, имеющих ортогональную систему собственных векторов (например, эрмитовых матриц), сходимость вблизи корня, будет даже кубической. Заметим, что допускать слишком точное совпадение 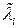 с собственным значением нельзя, ибо матрица системы (8.13) становится плохо обусловленной; в связи снахождением собственных векторов. Поэтому, когда в ходе итераций у величины
с собственным значением нельзя, ибо матрица системы (8.13) становится плохо обусловленной; в связи снахождением собственных векторов. Поэтому, когда в ходе итераций у величины 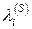 устанавливаются (т. е. перестают меняться) 5—7 знаков, то итерации следует прекращать.
устанавливаются (т. е. перестают меняться) 5—7 знаков, то итерации следует прекращать.
Замечание 8.2.. Переменный сдвиг собственного значения (8.13) нельзя включать с первой итерации; сначала надо получить грубую сходимость итераций с постоянным сдвигом.
Замечание 8.3. Обратные итерации особенно удобны, если матрица заранее приведена преобразованием подобия к почти треугольной форме. Тогда одна обратная итерация выполняется методом, исключения с выбором главного элемента всего за 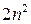 действий. Теоретически для ленточных матриц возможна еще большая экономия, но преобразование подобия почти треугольной матрицы к трехдиагональной форме не всегда устойчиво.
действий. Теоретически для ленточных матриц возможна еще большая экономия, но преобразование подобия почти треугольной матрицы к трехдиагональной форме не всегда устойчиво.
Выводы. Обратные итерации с постоянным и особенно с переменным сдвигом — очень эффективный метод расчета. Для нахождения собственных векторов этот метод считается наиболее точным. Сходимость при хорошем подборе 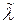 настолько быстрая, что метод пригоден и для близких или случайно равных по модулю собственных значений (ибо после сдвига они хорошо различаются), и даже при наличии у матрицы нелинейного элементарного делителя.
настолько быстрая, что метод пригоден и для близких или случайно равных по модулю собственных значений (ибо после сдвига они хорошо различаются), и даже при наличии у матрицы нелинейного элементарного делителя.
Все перечисленные методы реализованы на ЭВМ и их можно найти в пакетах прикладных программ, например: MathCAD, MathLAB.
| <== предыдущая страница | | | следующая страница ==> |
| ММ-8. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТИЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ КВАДРАТНОЙ МАТРИЦЫ | | | Критерий усвоения |
Дата добавления: 2014-04-15; просмотров: 673; Нарушение авторских прав

Мы поможем в написании ваших работ!