Глава 7. Показатели вариации в статистике

вступление

В процессе статистического анализа может сложиться ситуация, когда значения средних величин совпадают, а совокупности, на основе которых они рассчитаны, состоят из единиц, значения признака у которых достаточно резко различаются между собой. Возьмем, например, данные о количестве договоров, заключенных в двух филиалах страховой компании. Предположим, что в каждом из филиалов работает по два агента. В первом филиале один агент заключил 5 договоров, а второй – 25; во втором филиале каждый агент заключил по 15 договоров. Как видим, среднее число договоров, заключенных одним агентом в каждом филиале совпадает (15 договоров), в то же время очевидно, что первая и вторая совокупности качественно неоднородны, т. е. вариация значений признака внутри них различна.

7.1. Абсолютные и относительные показатели вариации

Вариациейназывается изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака

R = x_max - x_min.

Среднее линейное отклонение () представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение

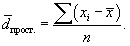
Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:

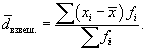
Дисперсией (s²) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней:

- для несгруппированных данных:

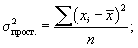
- для сгруппированных данных:

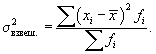
Квадратный корень из дисперсии называется средним квадратическим отклонением(его называют также стандартным отклонением):

- для несгруппированных данных:

- для сгруппированных данных:

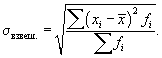
Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:

- коэффициент осцилляции:

- относительное линейное отклонение:

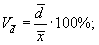
- коэффициент вариации:

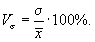
Принято считать, что если значение V_s > 33%, то совокупность неоднородна, и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во всех видах статистического анализа).

Рассмотрим две совокупности сотрудников рекламных агентств.

Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.

Таблица 7.1 – Распределение сотрудников первого агентства по уровню месячной заработной платы

Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.

Таблица 7.2 – Распределение сотрудников второго агентства по уровню месячной заработной платы

Рассчитаем средний уровень заработной платы:

- для первого агентства:

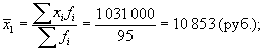
- для второго агентства:

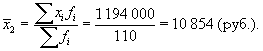
Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.

Рассчитаем показатели вариации для приведенных в табл. 7.1 и 7.2 вариационных рядов (табл. 7.3 и 7.4).

Таблица 7.3 – Расчет абсолютных и относительных показателей вариации для первого агентства

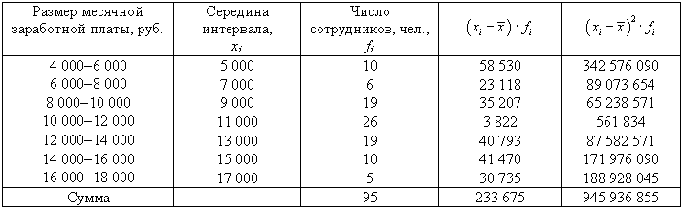
По первому агентству получим следующие данные.

Размах вариации:

R = x_max - x_min = 18 000 - 4000 = 14 000 (руб.).

Среднее линейное отклонение (так как ряд сгруппирован и частоты не равны между собой) рассчитываем как взвешенную величину:

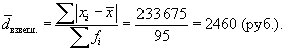
Дисперсия:

Среднее квадратическое отклонение:

Коэффициент осцилляции:

Относительное линейное отклонение:

Коэффициент вариации:

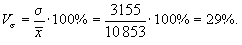
Судя по коэффициенту вариации, совокупность по данному признаку можно считать однородной.

Проведем расчет аналогичных характеристик вариации по второму агентству (табл. 7.4).

Таблица 7.4 – Расчет абсолютных и относительных показателей вариации для второго агентства

Показатели вариации по второму агентству:

Размах вариации:

R = 22 500 - 1500 = 21 000 (руб.);

Среднее линейное отклонение:

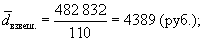
Дисперсия:

Среднее квадратическое отклонение – 5180 (руб.).

Коэффициент осцилляции – 193%.

Относительное линейное отклонение – 40%.

Коэффициент вариации – 48%.

Таким образом, по данному признаку вторая совокупность сотрудников неоднородна.

Сравнение относительных показателей вариации по двум совокупностям говорит о том, что дифференциация по уровню заработной платы во втором агентстве гораздо выше, чем в первом, хотя их средние практически совпадают между собой.

Дата добавления: 2014-04-24; просмотров: 1092; Нарушение авторских прав

Мы поможем в написании ваших работ!