Распределение скоростей и касательных напряжений в щелевом зазоре

После интегрирования полученного дифференциального уравнения получим:

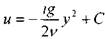
Величина постоянной интегрирования может быть получена исходя из условия, что скорость на гране пластины равна 0, т.е. при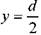, и = 0 . ^

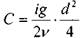5

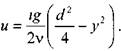
В центре потока скорость будет максимальной, т.е. при у = О

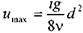
Вычислим величину средней скорости потока, для чего найдём величину расхода че­рез щель. Элементарный поток жидкости dQ в тонком слое dy будет равен:

откуда: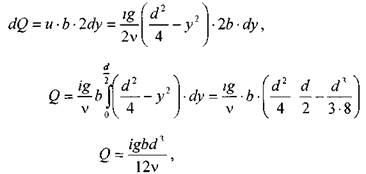

откуда средняя скорость в потоке.

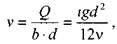
т.е. для потока в тонкой щели соотношение между средней скоростью и максимальной иное, чем в круглой трубе: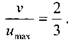

Потери напора будут равны.

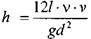3

Если одна из пластин будет двигаться относительно другой неподвижной пластины с постоянной скоростью, а давление в щели будет постоянным по всей длине, то при таком параллельном перемещении движущаяся пластина будет увлекать за собой жидкость. Та­кое перемещение жидкости называется безнапорным фрикционным движением. Выделим

в этом потоке элементарный объём жид­кости также в виде параллелепипеда.

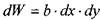
Поскольку величины сил давления на левую и правую боковые грани оди­наковы, то для равновесия необходимо, чтобы и силы трения, действующие 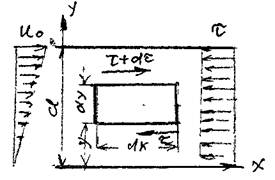вдоль верхней и нижней граней выде­ленного отсека тоже были одинаковыми.

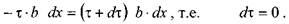
_f 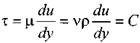j

После интегрирования получим:

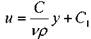
Величины постоянных интегрирования получим при следующих условиях:

при у = О и - 0 , при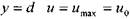

Следовательно: 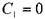и,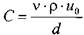т.е. будем иметь закон распределения

скоростей по сечению зазора

Таким образом, скорость по сечению зазора распределяется по линейному закону. Величина касательных напряжений постоянна по сечению зазора:

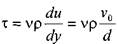
Тогда сила трения, действующая на пластину, будет равна:

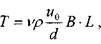
расход жидкости через зазор:

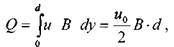
т.е. средняя скорость фрикционного потока равна половине максимальной скорости:

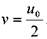
Выводы, полученные для плоских пластин легко перенести на криволинейные по­верхности, если допустить, что радиус кривизны такой поверхности бесконечно велик по сравнению с шириной зазора, что соответствует действительности.

В то время, когда жидкость проникает в узкую щель между неподвижными стенками за­зора, на поверхности стенок происходит адсорбция поляризованных молекул жидкости, обусловленная силами межмолекулярного взаимодействия. В результате этого на поверх­ности стенок образуется фиксированный слой жидкости, обладающий значительной прочностью на сдвиг, а живое сечение щели уменьшается. Это явление носит название облитерации Интенсивность облитерации зависит от свойств жидкости. Сложные по строению высокомолекулярные жидкости обладают значительно большей степенью обли­терации, по этой причине разного рода смазки являются подходящим средством для уп­лотнения соединений и устранения возможных утечек.

Явление облитерации необходимо учитывать при запуске оборудования, когда при­ходится преодолевать дополнительные усилия на страгивание простаивающих элементов оборудования.

Дата добавления: 2014-02-26; просмотров: 338; Нарушение авторских прав

Мы поможем в написании ваших работ!