Рабочих программ анализа

Преобразование математических моделей в процессе получения

Реализация функциональных математических моделей различных иерархических уровней как системы уравнений определенного типа на ЭВМ подразумевает выбор численного метода решения уравнений и преобразования уравнений в соответствии с особенностями выбранного метода. Конечная цель преобразований - получение рабочей программы анализа в виде последовательности элементарных действий (арифметических и логических операций), реализуемых командами ЭВМ. Все преобразования исходной математической модели ЭВМ выполняет автоматически по специальным программам, пользователю нужно лишь указать те программы, которые он хочет использовать. Этот процесс можно представить в виде иллюстрации (рис 14.3). На рисунке 14.3 показан процесс преобразований математической модели, относящихся к различным иерархическим уровням.

Ветвь 1 постановка задачи на микроуровне в виде ДУЧП. Методы решения ДУЧП основаны на:

1) дискретизации, заключающейся в замене непрерывных переменных конечным множеством их значений в заданных для исследования пространственном и временном интервалах;

2) алгебраизации - замене производных алгебраическими соотношениями.

Применяют различные способы дискретизации и алгебраизации переменных при решении ДУЧП. Если ДУЧП стационарное (то есть описывает статические состояния), то дискретизация и алгебраизация преобразует ДУЧП в систему алгебраических уравнений (АУ), в общем случае нелинейных (ветвь 2). Если ДУЧП нестационарное (то есть описывает изменяющиеся во времени и пространстве поля переменных), то дискретизацию и алгебраизацию можно представить состоящей из двух этапов:

1) устранение производных по пространственным координатам (ветвь 3), результат система ОДУ;

2) устранение производных по времени (ветвь 4).

Ветвь 5 непосредственное решение нелинейных АУ различными методами. Ветвь 6 линеаризация уравнения.

Ветвь 7 решение системы ЛАУ с помощью прямых методов (метод Гаусса и др.).

Ветвь 8 преобразование исходного описания задачи, относящейся к макро уровню, к системе ОДУ с известными н.у. Если это система нелинейных ОДУ, то дальнейшие преобразования по ветвям 4,6,7 или 4,5; если же система линейных ОДУ, то непосредственный переход к системе ЛАУ (ветвь 9).

Для анализа объектов на метауровне применяют либо переход к системе ОДУ (ветвь 10), либо переход к системам логических уравнений, моделям массового обслуживания или аналитическим моделям, отображающим упрощенно технико-экономические показатели объекта (ветвь 11). Сведение этих форм моделей в последовательность элементарных вычислительных операций (ветвь 12) не вызывает затруднений.

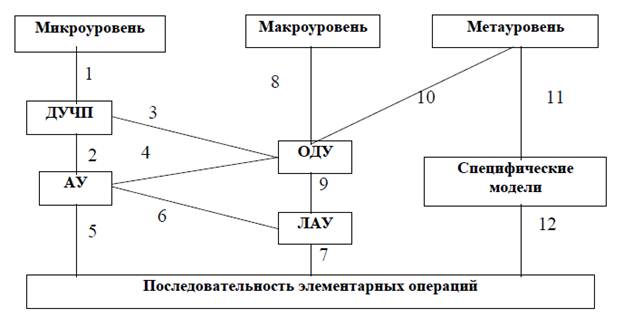
Рис. 14.3. Преобразование математических моделей с разных иерархических уровней

Дата добавления: 2014-02-26; просмотров: 622; Нарушение авторских прав

Мы поможем в написании ваших работ!