Методика получения математических моделей элементов

Классификация математических моделей

1. По характеру отображаемых свойств.

1.1 Структурные математические модели предназначены для отображения структурных свойств объекта. Различают топологические и геометрические математические модели.

1.1.1 В топологических математических моделях отображаются

состав и взаимосвязь элементов объекта. Их чаще всего применяют для

описания объектов, состоящих из большого числа элементов, при решении задач привязки конструктивных элементов к определенным пространственным позициям (компоновка оборудования, составление расписания). Может иметь форму графов, таблиц, матриц и т.п.

1.1.2 Геометрические математические модели отображают геометрические свойства объекта. Помимо сведений о взаимном расположении элементов содержатся сведения о форме деталей. Геометрические математические модели могут выражаться совокупностью уравнений линий и поверхностей, графами и списками и т.п. Применяют при решении задач конструирования, оформления конструкторской документации. Используют несколько типов геометрических математических моделей.

Для отображения свойств деталей с несложными поверхностями

применяют аналитические и алгебрологические математические моде-

ли.

1.1.2.1 Аналитические математические модели это уравнения по-

верхностей и линий. Например: плоскость Ax+By+Cz+D=0; прямая

Ax+By+C=0 и др.

1.1.2.2 Алгебрологические математические модели - геометрические тела описываются системами логических выражений, отражающих условия принадлежности точек внутренним областям тел.

Для сложных поверхностей эти модели оказываются слишком громоздкими, поэтому используются каркасные и кинематические математические модели .

1.1.2.3 Каркасные математические модели представляют собой каркасы -конечные множества элементов принадлежащих поверхности. Поверхность разбивается на отдельные участки. Каждый можно аппроксимировать (например: ломаную линию на соответствующие кривые) поверхностями с простыми уравнениями.

1.1.2.4 Кинематические математические модели - поверхность

представляется в параметрическом виде R(u,v), где R=(x,y,z); u,v параметры. Такую поверхность можно получить как результат перемещения в трехмерном пространстве кривой R(u) (образующей) по некоторой

направляющей линии R(v). Коэффициенты уравнений во всех рассмотренных моделях, как правило, не имеют простого геометрического смысла, что неудобно. Этот недостаток устраняется в канонических моделях и геометрических макромоделях.

1.1.2.5 Канонические математические модели используются, когда удается выделить параметры, однозначно определяющие геометрический объект и имеющий простую связь с его формой. Пример: плоский многоугольник -координаты вершин.

Рис.14.1. Классификация математических моделей

1.1.2.6 Геометрические макромодели - описания предварительно

отображенных типовых геометрических фрагментов. Например: фраг-

менты - типовые сборочные единицы, макромодели - условные номера,

габаритные, стыковочные размеры. При оформлении конструкторской

документации макромодели используют для описания типовых графи-

ческих изображений (зубчатых колес, винтовых соединений, подшип-

ников и т.д.).

1.2 Функциональные математические модели отражают физическое или информационное состояние объекта или процессы изменения состояния. Обычно это система уравнений, связывающая фазовые переменные, внутренние, внешние и выходные параметры.

Выделение аспектов описаний приводит к выделению соответствующих математических моделей: электрических, механических, гидравлических, химических и пр.

2. По принадлежности к иерархическому уровню.

2.1 Математические модели на микроуровне отражают непрерывные процессы, протекающие в непрерывном пространстве и времени. Типичные математические модели на микроуровне - дифференциальные уравнения в частных производных (ДУЧП). Независимые переменные - пространственные коэффициенты и время. Пример: уравнение

теплопроводности

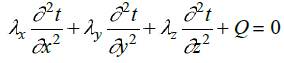
С помощью ДУЧП рассчитываются поля механических напряжений и деформаций, электрических потенциалов, давлений, температур и прочее, то есть отдельные детали сложных процессов в многокомпонентных средах. Анализировать такие процессы целиком с помощью ДУЧП очень трудоемко из-за громоздкости модели и следовательно, больших затрат машинных

ресурсов.

2.2 Математические модели на макроуровне используют укрупненную дискретизацию пространства по функциональному признаку (не обязательно отражение физической сущности процесса). Математические модели на макроуровне представляются в виде систем обыкновенных дифференциальных уравнений (ОДУ). Независимые переменные -

время, зависимые фазовые переменные, характеризующие состояние

укрупненных элементов дискретизированного пространства. Пример:

конденсатор

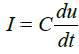
Примеры переменных: силы и скорости механических систем; напряжения и силы тока электрических систем; давления и расходы гидравлических и пневматических систем. Системы ОДУ пригодны для анализа и динамических и статических состояний объекта. Порядок системы уравнений зависит от числа выделенных элементов объекта. Если порядок 10³, то оперирование моделью становится затруднительным и необходимо переходить к представлениям на метауровне.

2.3 В математических моделях на метауровне в качестве элементов принимаются достаточно сложные совокупности деталей. Используются различные типы MM. Для многих объектов на метауровне математические модели представляют собой ОДУ, как и в предыдущем случае.

Иногда удается использовать специфические возможности функционирования объектов. Пример: цифровая техника. Переменные (напряжения и токи) могут быть представлены дискретно. В результате математическая модель становится системой логических уравнений, описывающих процессы преобразования сигналов. Очевидно, что такая математическая модель более экономична, чем та, в которой напряжения и

токи рассматривались бы как непрерывные. Важный класс - модели

массового обслуживания, применяемые для описания процессов функционирования информационных и вычислительных систем, производственных участков, линий, цехов.

3. По степени детализации описания в пределах одного уровня.

3.1 Полная математическая модель - модель, в которой фигурируют фазовые переменные, характеризующие состояние всех элементов объекта.

3.2 Макромодель - математическая модель, в которой отображаются состояния значительно меньшего числа межэлементных связей,

что соответствует описанию объекта при укрупненном выделении элементов. Понятия полная - и макро - математическая модель условные.

4. По способу представления свойств объекта.

4.1 Аналитические математические модели явные выражения

выходных параметров как функций внутренних и внешних параметров.

Высокая экономичность, но трудно получить, приходится принимать

существенные допущения и ограничения, отсюда снижение точности и

сужение области адекватности.

4.2 Алгоритмические математические модели выражают связь выходных параметров с внутренними и внешними в форме алгоритма.

Пример: уравнение с вектором фазовых переменных + алгоритм чис-

ленного метода решения + алгоритм вычисления вектора выходных па-

раметров.

4.3 Имитационные математические модели - разновидность алгоритмической модели, отражающая поведение исследуемого объекта во времени при задании внешних воздействий на объект. Пример: модели динамических объектов в виде систем ОДУ и модели систем массового обслуживания заданные в алгоритмической форме.

5. По способу получения модели.

5.1 Неформальные методы применяют на различных иерархических уровнях для получения математических моделей элементов. Эти методы включают в себя: изучение закономерностей процессов явлений, выделение существенных факторов, принятие и обоснование допущений, математическая интерпретация сведений и т.п. Применение неформальных методов, возможно для синтеза теоретических и эмпирических MM.

5.1.1 Теоретические математические модели создаются в результате исследования процессов и их закономерностей.

5.1.2 Эмпирические математические модели в результате изучения внешних проявлений свойств объекта с помощью измерений фазовых переменных и обработки результатов измерений.

5.2 Формальные методы применяют для получения математических моделей систем при известных математических моделях элементов.

Процедура получения математических моделей элементов включает в себя следующие операции:

1. Выбор свойств объекта, подлежащих отражению в модели. Этот

выбор основан на анализе возможных применений модели и определяет

степень универсальности математической модели.

2. Сбор исходной информации о выбранных свойствах объекта.

Источниками сведений могут быть опыт и знания инженера, научно-

техническая литература, результаты экспериментов.

3. Синтез структуры математической модели. Структура математической модели общий вид математических соотношений модели без конкретизации числовых значений параметров. Структура математической модели может быть также представлена в графической форме (эквивалентная схема, граф).

4. Расчет числовых значений параметров математической модели.

Эта задача ставится как задача минимизации погрешности модели заданной структуры, то есть

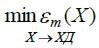
где Х вектор параметров модели; ХД область изменения параметров. 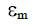определяется в соответствии с формулами (1) и (2)

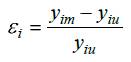
а скаляр направления

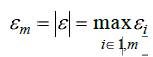
где yim функция, зависящая от x, а yiист. Определяется по результатам экспериментов. При этом эксперименты могут быть физическими, либо численными с применением более точных математических моделей, если таковые имеются в иерархическом ряду.

5. Оценка точности и адекватности математической модели. Для оценки точности, должны использоваться yiист., которые не использовались в предыдущем пункте. Большую ценность представляют не оценки

погрешностей Em , выполненные в одной-двух случайных точках про-

странства внешних переменных, а сведения об области адекватности

(ОА). Это требует больших затрат машинного времени. Поэтому расчет

ОА выполняется только при тщательной обработке математической модели унифицированных элементов, предназначенных для многократного применения.

Операции 2-5 этой методики могут выполняться многократно в процессе последовательного приближения к желаемому результату.

Так как расчет и представление сведений об ОА в многомерном пространстве затруднительны, то используют аппроксимации области адекватности (АОА). Для человека наиболее удобны АОА в виде вписанного в ОА гиперпараллелепипида со сторонами, параллельными координатным осям. Графическая иллюстрация ОА и АОА для двумерного пространства внешних переменных Q = (q1, q2), будет выглядеть в виде (рис. 12.1.), где ОА ограничена линиями i=1, i=2 и i=3, задаваемыми

уравнениями 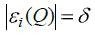, i=1,2,3. АОА выделена на рисунке штриховкой.

Сведения об АОА представляются в виде диапазонов изменения

внешних переменных, в которых модель адекватна (с точностью ):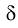

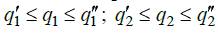. Другой возможной формой АОА является область, получаемая из ОА с помощью линеаризации ее границ. Линеаризация - метод рассмотрения нелинейных систем, при котором, при некоторых допущениях, они рассматриваются как линейные.

Такая форма неудобна для восприятия человеком, но предпочтительна при автоматическом контроле адекватности модели в процессе вычислений на ЭВМ.

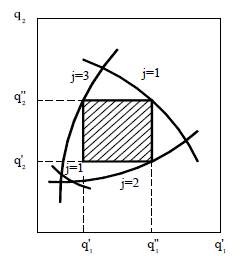
Рис.14.2 Область адекватности модели

Дата добавления: 2014-02-26; просмотров: 1057; Нарушение авторских прав

Мы поможем в написании ваших работ!