
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МОДЕЛЬ СОВЕРШЕННОЙ КОНКУРЕНЦИИ
Спрос на определенный товар отдельно взятого потребителя называется индивидуальным; всех потребителей, находящихся на выделенном рынке – совокупным.
Процесс построения совокупного спроса проиллюстрируем для квазилинейной функции полезности. Кривая индивидуального спроса задается уравнением:
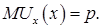
Процеес построения кривой совокупного спроса иллюстрируется на рис. 6.2.

Рисунок 6.2 – Построение кривой совокупного спроса
Кривая совокупного спроса получается из кривых индивидуального спроса путем их горизонтального суммирования. Кривая 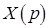 показываетколичество товара, который потребители приобретут по цене р. Кривая
показываетколичество товара, который потребители приобретут по цене р. Кривая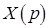 называется также кривой прямого спроса. Наряду с кривой прямогоспроса часто используется обратная к ней функция
называется также кривой прямого спроса. Наряду с кривой прямогоспроса часто используется обратная к ней функция 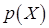 , которая называется кривой обратного спроса.
, которая называется кривой обратного спроса.
Пример.
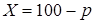 – функция прямого спроса;
– функция прямого спроса;
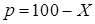 – функция обратного спроса.
– функция обратного спроса.
Легко видеть, что кривая совокупного спроса в общем случае будет более эластичной, чем кривая индивидуального спроса.
В случае большого числа потребителей (т.е. практически всегда) получение кривой совокупного спроса путем суммирования спроса отдельных потребителей вряд ли возможно. На практике для построения функции совокупного спроса используются два метода: метод репрезентативного потребителя и метод интегрирования.
Метод репрезентативного потребителя поясним на примере многострадальной функции Кобба-Дугласа.
Пример. На рынке находится N потребителей, предпочтения которых задаются функцией полезности 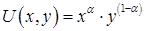 ; доходы потребителей составляют
; доходы потребителей составляют 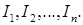
Для i-го потребителя спрос на товар х задается формулой
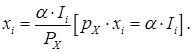
Тогда совокупный спрос составит
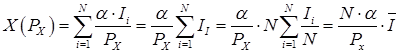 ,
,
где 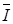 – средний доход потребителей.
– средний доход потребителей.
Потребитель с доходом равным 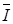 потребляет
потребляет 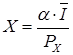 , т.е. в данном примере рынок ведет себя так, как если бы он состоял из N одинаковых потребителей с доходом, равным
, т.е. в данном примере рынок ведет себя так, как если бы он состоял из N одинаковых потребителей с доходом, равным 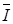 .
.
В этом случае говорят, что потребитель с доходом, равным 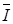 , является репрезентативным для данного рынка, а предпочтения рынка в целом описываются предпочтениями репрезентативного потребителя.
, является репрезентативным для данного рынка, а предпочтения рынка в целом описываются предпочтениями репрезентативного потребителя.
Репрезентативный потребитель существует не всегда. Когда отыскать репрезентативного потребителя не удается, применяется метод интегрирования.
Предположим, функция полезности потребителя известна с точностью до вектора параметров  . Предположим, что на множестве N потребителей распределение значений
. Предположим, что на множестве N потребителей распределение значений  характеризуется совместной плотностью распределения
характеризуется совместной плотностью распределения 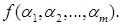 Тогда, если известен спрос для отдельно взятого потребителя с параметром
Тогда, если известен спрос для отдельно взятого потребителя с параметром 
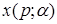 совокупный спрос будет равен
совокупный спрос будет равен
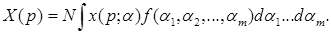
Аналитическое вычисление интеграла часто оказывается невозможным. В этом случае используются методы имитационного моделирования.
МОДЕЛЬ СОВЕРШЕННОЙ КОНКУРЕНЦИИ
8.1 Поведение фирмы на конкурентном рынке
Говорят, что на рынке имеет место совершенная конкуренция, если выполняется следующее условие:
- каждая фирма считает, что ее действия не приведут к изменению рыночной цены продукции и поэтому считает цену экзогенно заданной;
- все фирмы на рынке производят однородную продукцию;
- не существует преград к входу новых предприятий на рынок и прекращению деятельности существующих предприятий;
- все участники рынка имеют полную информацию, в частности, о ценах.
Обозначим рыночную цену продукции через p.
Поскольку фирма на конкурентном рынке не может влиять на рыночную цену выпускаемой ею продукции, задача конкурентной фирмы сводится к выбору объема выпуска продукции, который позволит получить максимальную прибыль:
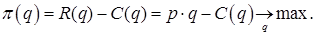
Необходимым условием максимума является равенство нулю производной от функции прибыли:
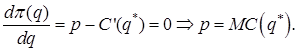
Экономическая интерпретация формулы иллюстрируется на рис. 8.1 и 8.2. Рис. 8.1 показывает, что оптимальная прибыль будет получена предприятием при таком объеме выпуска, при котором наклон функции выручки (равный p) будет равен наклону функции издержек (равному МС). Рис.8.2 иллюстрирует правило : предприятие должно увеличивать объем выпуска продукции до тех пор, пока рыночная цена продукции превышает (возрастающие краткосрочные) издержки, связанные с изготовлением дополнительной единицы продукции (т.е. пока 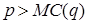 ).
).
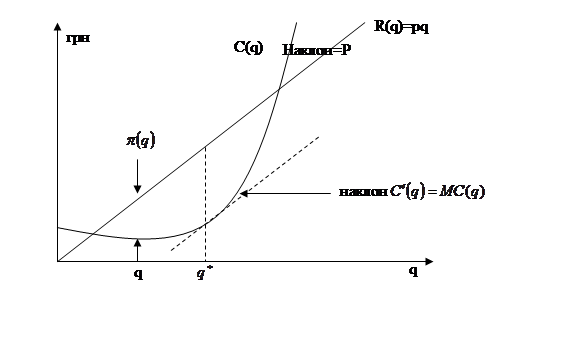 Рисунок 8.1 – Определение оптимального объема выпуска продукции
Рисунок 8.1 – Определение оптимального объема выпуска продукции
 Рисунок 8.2 – Экономическая интерпретация фомулы
Рисунок 8.2 – Экономическая интерпретация фомулы
Заметим, что формула показывает оптимальный объем выпуска продукции, но ничего не говорит о том, будет ли полученная прибыль положительной! Очевидно, при отрицательной прибыли фирме стоит задуматься о прекращении выпуска продукции, т.е. установить 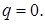 Напомним, что издержки предприятия складываются из постоянных и пременных издержек:
Напомним, что издержки предприятия складываются из постоянных и пременных издержек: 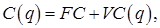 и рассмотрим эти две альтернативы.
и рассмотрим эти две альтернативы.
1) 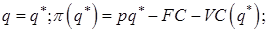
2) 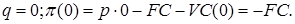
Первый вариант будет предпочтительнее, если:
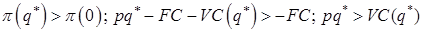
или
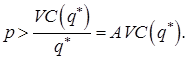
Таким образом, конкурентное предприятие будет выпускать продукцию только в том случае, когда рыночная цена будет превышать средние переменные издержки, связанные с изготовлением единицы продукции.
Полученную предприятием прибыль удобно изобразить графически следующим образом (рис. 8.3). Преобразуем следующим образом:
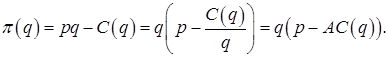
|
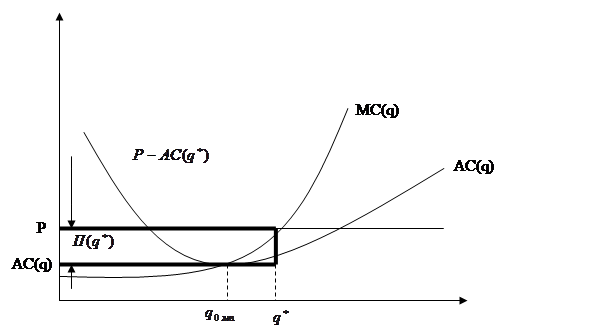 Рисунок 8.3 – Прибыль конкурентного предприятия
Рисунок 8.3 – Прибыль конкурентного предприятия
Тогда прибыль будет равна площади заштрихованого прямоугольника на рис. 8.3.
| <== предыдущая страница | | | следующая страница ==> |
| Индивидуальный спрос и совокупный спрос | | | Конкурентное равновесие |
Дата добавления: 2014-07-14; просмотров: 302; Нарушение авторских прав

Мы поможем в написании ваших работ!