
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВНЫЕ КОНЦЕПЦИИ ТЕОРИИ ИГР
Ценовой дискриминацией называется ценовая стратегия при которой различные покупатели платят различные цены за один и тот же товар.
Предположим, монополист может неким образом узнать максимальную цену, которую потребитель согласен заплатить за товар (резервированную цену потребителя). Стратегия ценообразования, при которой монополист назначает каждому потребителю его резервированню цену, называется совершенной ценовой дискриминацией (или дискриминацией 1-го рода) (рис. 9.4).
|
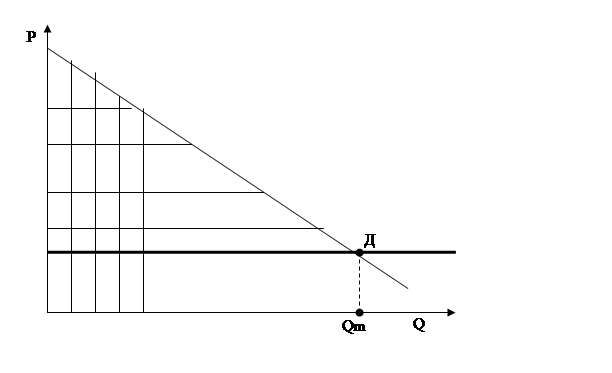 Рисунок 9.4 – Совершенная ценовая дискриминация
Рисунок 9.4 – Совершенная ценовая дискриминация
В этом случае монополист получит в качестве прибыли весь потенциально возможный общественный излишек (заштрихованная область на рис.9.4). В случае совершенной ценовой дискриминации объем выпуска продукции и общественный излишек для монополии будет таким же, как и для конкурентной отрасли. Однако в случае свободной конкуренции весь общественный излишек достанется потребителям, а в случае дискриминирующей монополии –производителю.
Совершнная ценовая дискриминация – теоретическая абстракция. Однако существует ряд стратегий, позволяющих монополисту получить результат, сравнимый с совершенной дискриминацией.
Для того, чтобы стратегии ценовой дискриминации были реализуемы, чтобы была исключена возможность арбитража, т.е. покупки товара по более низкой цене с последующей перепродажей его по более высокой цене. Поэтому ценовая дискриминация чаще всего практикуется на рынках услуг.
Различают 3 типа ценовой дискриминации:
1) 1-го рода – совершенная ценовая дискриминация;
2) 2-го рода – нелинейное ценообразование (ситуация, в которой цена единицы продукции зависит от объема покупки);
3) 3-го рода – сегментация рынка (ситуация в которой потребители могут быть отнесены к разным сегментам по критериям, доступным наблюдению монополиста, и для каждого сегмента может быть установлена отдельная цена).
Рассмотрим пример ценовой дискриминации 3-го рода.
Пример. В университетском кинотеатре 100 мест. Типичный сеанс посещают 80 студентов и 20 преподавателей. Резервированная цена билета у студентов составляет 10 грн., а у преподавателей – 20 грн. Себестоимость просмотра фильма примем равной нулю.
Без ценовой дискриминации у кинотеатра было бы две возможности: установить цену билета в 10 грн. и привлечь всех потенциальных потребителей, или установить цену в 20 грн. и обслуживать только преподавателей. Сравним прибыль каждой из этих стратегий:

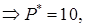
т.е. кинотеатр обслуживал бы всех потребителей по цене 10 грн. за билет.
Применяя ценовую дискриминацию 3-го рода, кинотеатр может назначить регулярную цену билета в 20 грн. и предоставлять 50-процентную скидку студентам по предъявлении студенческого билета. Прибыль такой стратегии составит
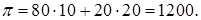
Заметим, что в результате предоставления скидки студенты ничего не выигрывают в сравнении с предыдущим сценарием – скорее, от наличия скидок проигрывают преподаватели. Это достаточно общее правило: скидки устанавливаются не для «помощи» малообеспеченным покупателям, а для повышения регулярной цены для всех остальных.
В качестве примера ценовой дискриминации 2-го рода рассмотрим стратегию, известную как линейный (или двухчастный) тариф. При использовании линейного тарифа потребители платят фиксированную сумму F за право приобрести товар или услугу и определенную расценку r за единицу приобретаемого ими товара. Примером могут служить телефонные компании, взымающие с потребителей абонентскую плату и плату за каждую минуту разговора.
При использовании линейного тарифа общие затраты потребителя при приобретении q единиц продукции составят 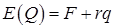 , а цена единицы продукции будет равна
, а цена единицы продукции будет равна
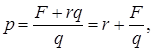
т.е. меняться в зависимости от объема закупок, что и объясняет использование термина «нелинейное ценообразование».
Рассмотрим применение линейных тарифов на примере.
Пример. Развлекательный парк взимает плату за вход F и плату за посещение аттракционов p. Спрос репрезентативного потребителя на аттракционы задается функцией 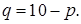 Издержки по обслуживанию одного посетителя на аттракционе равны 2 грн. Необходимо найти оптимальные значения F и p.
Издержки по обслуживанию одного посетителя на аттракционе равны 2 грн. Необходимо найти оптимальные значения F и p.
Структура оптимальной стратегии иллюстрируется на рис. 9.5.
| |
|
|
|
|
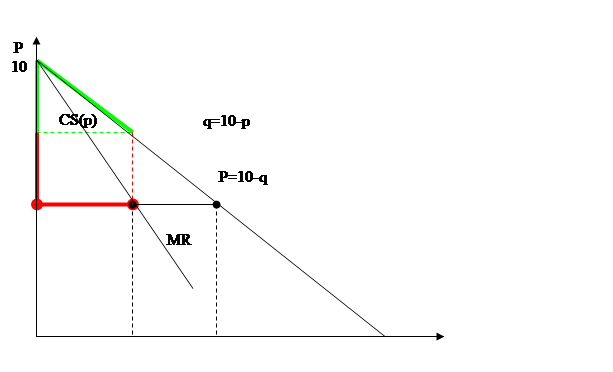
Рис. 9.5 – Использование линейного тарифа
При отсутствии ценовой дискриминации прибыль парка с каждого посетителя составила бы
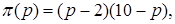
откуда легко получить, что оптимальная цена билета равна 6. По такой цене каждый потребитель посетит 10-6=4 аттракциона, а прибыль парка составит 4(6-2) = 16грн с каждого посетителя. При этом каждый потребитель получит излишек, равный площади заштрихованного на рис. 9.5 треугольника:
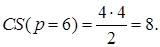
Следовательно, в качестве платы за вход можно установить сумму, не превышающую 8 грн. Поскольку прибыль парка прямо пропорциональна плате, взимаемой с каждого покупателя, очевидно F =8 грн.
Такая стратегия допустима, и позволяет увеличить прибыль, получаемую с каждого посетителя, до (16+8)=24 грн., но будет ли она оптимальной? Из предыдущей дискусси ясно, что назначая цену за билет, парк должен установить в качестве платы за вход 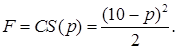 Прибыль парка складывается из двух частей: доходов от продажи билетов и платы за вход,
Прибыль парка складывается из двух частей: доходов от продажи билетов и платы за вход,
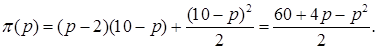
Дифференцируя по p, получим:
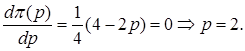
Таким образом, парк получит максимальную прибыль, продавая билеты по себестоимости! В этом случае все доходы парка будут состоять из собранной платы за вход, которая в свою очередь будет равна
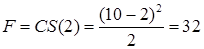 грн.
грн.
Действуя таким образом, парк извлечет из каждого потребителя весь его потребительский излишек, т.е. достигнет тех же результатов, что и при совершенной ценовой дискриминации.
ОСНОВНЫЕ КОНЦЕПЦИИ ТЕОРИИ ИГР
Игра N лиц характеризуется набором следующих элементов:
- множество игроков 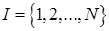 ;
;
- набор стратегий для каждого игрока 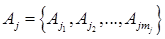 ;
;
- функциями выигрыша для всех игроков 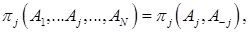 где
где 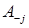 означает набор стратегий всех игроков, кроме j.
означает набор стратегий всех игроков, кроме j.
В случае, когда N=2, эту информацию удобно представить в виде таблицы, называемой платежной матрицей игры (рис. 10.1)
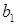
| ... | 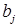
| ... | 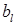
| |
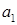
| 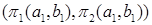
| ... | ... | ... | ... |
| ... | ... | ... | ... | ... | |
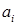
| ... | ... | 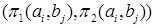
| ... | ... |
| ... | ... | ... | ... | ... | ... |
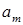
| ... | ... | ... | ... | 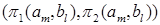
|
Рисунок 10.1 – Платежная матрица игры двух лиц
Концепции принятия решений в игровых ситуаций проиллюстрируем на примере нескольких классических игр.
Пример 1. Дилемма заключенного.
Рассмотрим следующую ситуацию. Две крупных компании, выпускающих однородную продукцию, – скажем, Пепси-Кола и Кока-Кола – делят рынок пополам, получая ежегодно по 2 млрд. долларов. Каждая из компаний имеет возможность провести широкомасштабную рекламную кампанию стоимостью 1 млрд. долларов. Если только одна из компаний воспользуется этой возможностью, то она завоюет весь рынок. Если же обе фирмы проведут рекламнную кампанию, ситуация на рынке не изменится[1].
Платежная матрица этой игры приведена на рис. 10.2. Каждый игрок имеет две стратегии: «+» – проводить рекламную компанию, «–» – не проводить.
| Пепси-Кола | |||
| – | + | ||
| Кока-Кола | – | (2;2) | (0;3) |
| + | (3;0) | (1;1) |
Рисунок 10.2 – Платежная матрица игры «дилемма заключенного»
Если Пепси-Кола не будет проводить реламную кампанию, то наилучшим выбором для Кока-Колы будет «+», поскольку в этом случае она получит 3 млрд. дол. вместо 2 млрд. Если же Пепси-Кола не собирается рекламировать свою продукцию, то лучшей стратегией для Кока-Колы опять-таки будет «+», поскольку в этом случае она получит 1 млрд. дол. вместо 0. Таким образом, вне зависимости от действий конкурента, наилучшей стратегией для Кока-Колы будет «+». Такая стратегия называется доминирующей.
Поскольку игра симметрична, «+» будет доминирующей стратегией и для Пепси-Колы. Поэтому следует ожидать, что обе компании предпочтут рекламировать свою продукцию и вероятным исходом игры будет (1;1). Парадокс состоит в том, что в данном случае компании в буквальном смысле слова выбрасывают деньги на ветер – обе компании получили бы лучший результат, отказавшись от рекламной кампании.
Теперь дадим общее определение. Стратегия а* игрока i называется доминирующей (слабо доминирующей), если прибыль игрока i при использовании стратегии а* будет больше (не меньше) его прибыли от использования любой другой стратегии вне зависимости от стратегий 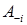 , выбранных другими игроками:
, выбранных другими игроками:
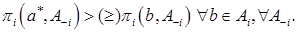
Если у каждого игрока есть доминирующая стратегия, то решение игры тривиально – каждый из игроков применит свою доминирующую стратегию. Исходом игры будет 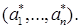
Пример 2. Битва полов (семейная драма).
В этой игре муж и жена решают, как лучше провести субботний вечер. Муж предпочел бы сходить на бокс; жена – посетить оперу. В любом случае главное для супругов – быть вместе; раздельное времяпрепровождение не принесет им никакого удовольствия. Платежная матрица этой игры представлена на рис. 10.3.
| Жена | |||
| Бокс | Опера | ||
| Муж | Бокс | (2;1) | (0;0) |
| Опера | (0;0) | (1;2) |
Рисунок 10.3 – Платежная матрица игры «Битва полов»
Легко видеть, что в данной игре ни у одной из сторон нет доминирующей стратегии. Тем не менее интуитивно очевидно, что супруги должны провести время вместе (хотя где именно – не ясно).
Такая ситуация является типичной. Основной концепцией выработки стратегия в подобных ситуациях является понятие равновесия по Нэшу.
Говорят, что исход 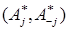 является равновесием по Нэшу в игре
является равновесием по Нэшу в игре 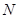 лиц, если
лиц, если
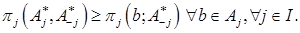
Игра находится в состоянии равновесия по Нэшу, если ни один из игроков не заинтересован в отклонении от ситуации равновесия в одностороннем порядке. В игре «битва полов» исход (бокс;бокс) является равновесием по Нэшу, т.к. ни мужу, ни жене невыгодно отклоняться от этой точки в одностороннем порядке. То же самое относится и к исходу (опера; опера).
Сущестствует еще один подход к описанию равновесия по Нэшу. Ввведем понятие функции реакции i-го игрока следующим образом:
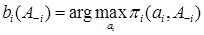
(эта конструкция называется также функцией наилучшего ответа, функцией отклика и т.д.). Функция реакции задает наилучшую стратегию i-го игрока против стратегий 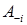 остальных игроков. Например, в игре «битва полов»
остальных игроков. Например, в игре «битва полов» 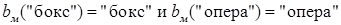 . Тогда исход
. Тогда исход 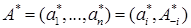 будет являться равновесием по Нэшу, если
будет являться равновесием по Нэшу, если
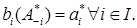
Т.е. в равновесии по Нэшу каждый игрок наилучшим образом отвечает на равновесные стратегии других игроков.
Записав уравнения в векторной форме, мы получим:
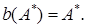
Уравнение позволяет интерпретировать равновесие по Нэшу как неподвижную точку отображения 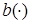 – понятие, с которым мы неоднократно сталкивались в курсе «Экономическая кибернетика».
– понятие, с которым мы неоднократно сталкивались в курсе «Экономическая кибернетика».
Всегда ли существует равновесие по Нэшу? Чтобы ответить на этот вопрос, рассмотрим
Пример 3. «Орел-решка».
В этой игре каждый из игроков скрытно от другого кладет монетку орлом или решкой вверх. Если результаты совпадают, первый игрок забирает монетку у другого. В противном случае – второй игрок забирает монетку у первого. Платежная матрица игры показана на рис. 10.4.
| орел | решка | ||
| орел | (1;1) | (-1;1) | |
| решка | (-1;1) | (1;-1) |
Рисунок 10.4 – Платежная матрица игры «орел-решка».
Из простого перечисления возможных исходов следует, что равновесия по Нэшу в этой игре не существует. В то же время очевидно, что в данной игре не имеет смысла пытаться перехитрить партнера – простое подбрасывание монетки даст ожидаемый выигрыш, равный нулю. Для описания подобных действий вводится понятие смешанной (или рандомизированной) стратегии.
Смешанной стратегией i-го игрока называется набор вероятностей 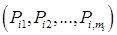 ,где
,где 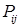 –вероятность применения игроком i стратегии j.
–вероятность применения игроком i стратегии j.
Теорема Нэша утверждает, что при достаточно общих предположениях в любой игре N лиц существует по крайней мере одно равновесие в простых или смешанных стратегиях.
Таким образом, в подавляющем большинстве встречающихся в экономике игр можно рассчитывать на существование по крайней мере одного равновесия по Нэшу. Часто проблема состоит скорее в том, что подобных равновесий оказывается слишком много. Существует обширная литература, посвященная разного рода «усовершенствованиям» концепции равновесия по Нэшу, призванная ограничить количество решений. Наиболее важным из подобных усовершенствований является понятие равновесия в под-играх (subgame-perfect Nash equilibrium) или равновесия по Зельтену (в честь его автора, Нобелевского лауреата Рейнхарда Зельтена).
Вернемся к игре «битва полов» и предположим, что игра происходит не одновременно, а последовательно: муж «ходит» после жены. Такие игры удобно изображать в виде дерева решений (рис. 10.5).
Очевидно, что право первого хода дает жене возможность выбрать «свое» равновесие по Нэшу, т.е. вероятным исходом игры будет вечер в опере.
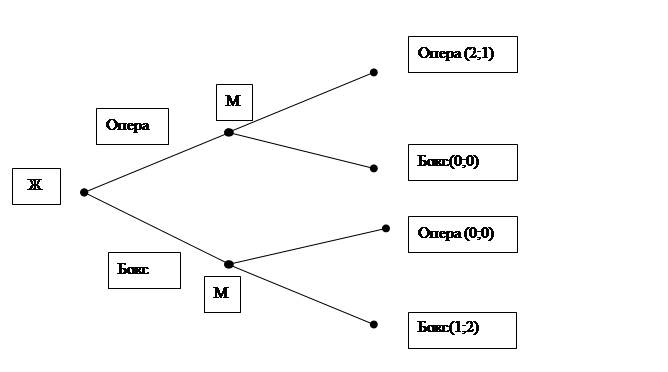

Рисунок 10.5 – Дерево решений в последовательной «битве полов»
Набор стратегий жены в этой игре остается неизменным, в то время как множество стратегий мужа существенно усложняется. Стратегия игрока должна предписывать его действия в любой из ситуаций, которые могут возникнуть в ходе игры. Поэтому возможной стратегией мужа может быть стратегия вида «бокс если бокс, опера если опера» (сокращенно ББОО). Таким образом, у мужа в этой игре будут четыре стратегии, а платежная матрица игры будет такой, как показано на рис. 10.6.
| БББО | ОББО | ББОО | ОБОО | |
| Опера | (0,0) | (0,0) | (2,1) | (2,1) |
| Бокс | (1,2) | (0,0) | (1,2) | (0,0) |
Рис 10.6 – Платежная матрица в последовательной «битве полов»
В игре, представленной на рис. 10.6, есть много равновесий по Нэшу – например, (бокс, БББО). Действительно, если муж настроен пойти на бокс в любом случае, то жене не остается ничего лучшего, чем смириться и пойти на бокс самой. В этом случае угроза мужа пойти на бокс, даже если жена выберет оперу, так и остается не более чем обещанием – до практической реализации угрозы дело не доходит. Выражаясь терминами теории игр, ветка «бокс если опера» находится вне пути игры.
Очевидно, что подобное поведение жены нерационально. При заданной структуре платежей, столкнувшись с выбором «опера», муж сам себя накажет, выбрав «бокс». Поэтому подобную угрозу можно считать неправдоподобной (non-credible threat) и не принимать во внимание.
Равновесием по Зельтену называется равновесие по Нэшу, не содержащее неправдоподобных угроз одного из игроков. Равновесие по Зельтену предполагает рациональный выбор каждого игрока в каждой ситуации, которая может возникнуть в ходе игры. Такой подход часто позволяет сузить множество решений конкретной игры.
В последовательной «битве полов» существует три равновесия по Нэшу, но только одно равновесие по Зельтену – (опера, ББОО).
[1] Подобная ситуация действительно имела место в 80-х годах прошлого века. Затраты обеих фирм на продвижение своих торговых марок при задействовании звезд эстрады первой величины были настолько велики, что этот эпизод вошел в историю под названием “rock-n-roll cola wars”.
| <== предыдущая страница | | | следующая страница ==> |
| Ценовая дискриминация. Ценовой дискриминацией называется ценовая стратегия при которой различные покупатели платят различные цены за один и тот же товар | | |
Дата добавления: 2014-07-14; просмотров: 750; Нарушение авторских прав

Мы поможем в написании ваших работ!