Парный линейный и нелинейный регрессионный анализ

Любую форму связи можно выразить уравнением общего вида y=f(x), где у – зависимая переменная (функция), а х – независимая переменная (аргумент).

Изменение зависимой переменной от одной или нескольких независимых называется регрессией. Известны эмпирические методы выравнивания (например, методом скользящей средней) и аналитические (линейное сглаживание и др.).

Линейная регрессия

При одной независимой переменной и корреляции уравнение линейной регрессии имеет вид:

y=a₀+a₁x₁ - прямая линия!

где y – ожидаемое значение функции,

а₀ – свободный член в уравнении регрессии,

а₁ – угловой коэффициент или коэффициент регрессии,

х₁ – значение независимой переменной.

Y

y=a₀+a₁x₁

a₁ a₁=r_xy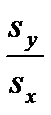

а₀

׀ ׀ ׀ ׀ ׀

0 1 2 3 4 5 X₁

Рис. 1. График прямолинейной регрессии

Нахождение уравнения линейной регрессии – это вычисление а₀ и а₁ на ПК. Оба этих параметра при корреляционной связи оцениваются с определенными статистическими ошибками, позволяющими установить значимость параметров а₀ и а₁.

Дата добавления: 2014-07-19; просмотров: 367; Нарушение авторских прав

Мы поможем в написании ваших работ!