
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Нелинейная регрессия
|
Читайте также: |
Полиномы второго и более высоких порядков
Уравнение прямой линии – частный случай полинома, это полином первой степени.
Полиномы больших степеней оказываются подчас лучше соответствующими исходным данным, и потому тоже используются.
Полином второй степени это квадратичная парабола
y= a0+a1x1 + a2x22.
В этом случае необходимо найти a0, a1 и a2 на ПК.
Прямая линия – частный случай квадратичной параболы, когда a2=0.
Y

Х
Рис. 2. Квадратичная парабола
В биологии, сельском и лесном хозяйствах квадратичная парабола обычно неплохо описывает связи: густота посева – урожайность, глубина заделки семян – урожайность и др. Во всех подобных случаях производственники должны найти оптимум фактора, обеспечивающего максимальную урожайность. Это так называемый поиск экстремума (рис. 2).
Парабола (полином ) третьего порядка описывается уравнением
y= a0+a1x1 + a2x22+ a3x33.
Она используется еще реже, а полиномы еще больших степеней в наших областях знаний практически не используются.
Гиперболы. Для аналитического сглаживания эмпирических рядов служат также гиперболы разных порядков с различным числом неизвестных.
Наиболее простая из них гипербола первого порядка вида:
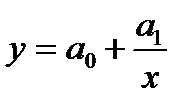
В ряде случаев именно так изменяется загрязнение почвы продуктами выхлопных газов автомобилей при изменении расстояния от автотрассы – источника загрязнения.
Y
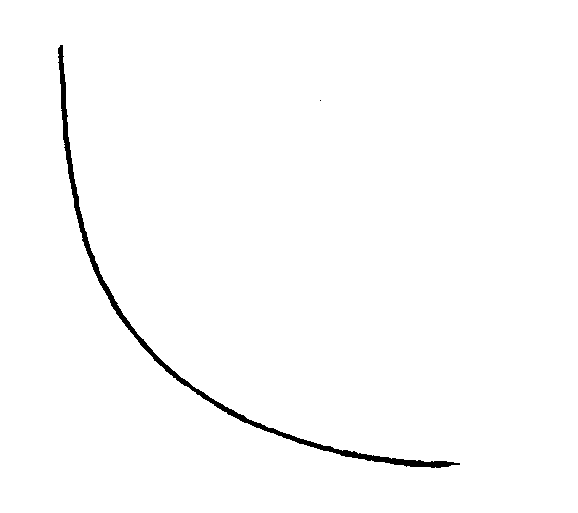
Х
Рис. 3. Гипербола первого порядка
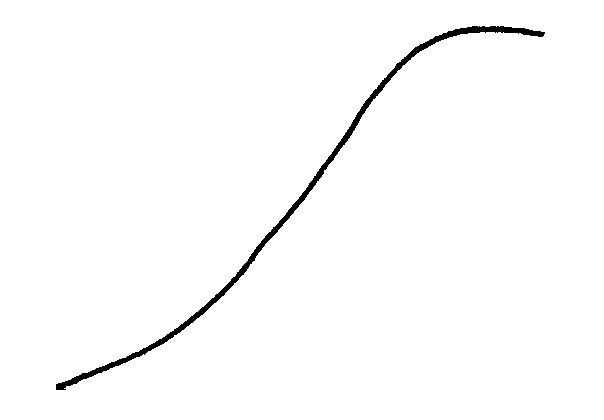
Регрессия, выражаемая уравнением логистической кривой
Логистическая кривая, называемая иногда S-образной, сигмоидной или кривой Сакса изображена на рис. 4.
Y
 X
X
Рис. 4. Логистическая кривая
Описывается уравнением Ферхлюста, которое здесь не приводится. Такие кривые хорошо описывают изменения во времени (Х – время) высоты растений (в т.ч. деревьев), их массы, числа особей популяции в замкнутом пространстве и т.п. Эти кривые называют поэтому также кривыми роста.
| <== предыдущая страница | | | следующая страница ==> |
| Парный линейный и нелинейный регрессионный анализ | | | Периодическая регрессия |
Дата добавления: 2014-07-19; просмотров: 352; Нарушение авторских прав

Мы поможем в написании ваших работ!