Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Парная регрессия
|
Читайте также: |
В зависимости от количества факторов , включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая регрессия представляет собой модель, где среднее значение зависимой переменной y рассматривается как функция одной независимой переменной 
, т.е. это модель вида
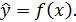
При построении регрессионных моделей могут использоваться как линейные, так и нелинейные функции.
Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Парная линейная регрессия
Линейная регрессия находит широкое применение в ЭММ ввиду четкой экономической интерпретации ее параметров.
Уравнение линейной регрессии имеет вид:
Это уравнение позволяет по заданным значениям фактора иметь теоретическое значение результативного признака подстановкой в него фактических значений фактора.
Предположим, выдвигается гипотеза о том, что величина спроса на товар y находится в зависимости от цены . Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. Так, если зависимость спроса y от цены характеризуется, например, уравнением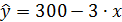 
, то это означает, что сростом цены на 1 д.е. спрос в среднем уменьшается на 3 ед. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией.
Параметр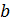 
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если функция издержек y (тыс. руб.) выражается как 
(- количество единиц продукции), то с увеличением объема продукции на одну единицу издержки производства возрастают в среднем на четыре тыс. рублей, т.е. дополнительный прирост продукции на одну ед. потребует увеличение затрат в среднем на 4 тыс. руб.
Знак при коэффициенте регрессии 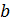показывает направление связи: при 
– связь прямая, при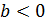 
– обратная.
Формально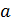 
- значение результативного признака y при значении фактора равном нулю (=0). Если фактор не может иметь нулевого значения, то трактовка свободного члена не имеет смысла. Параметр 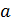может не иметь экономического содержания. Попытки экономической интерпретировать параметр 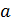могут привести к абсурду, особенно при 
.
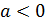Интерпретировать можно лишь знак при параметре 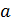. Если 
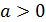, то относительное изменение результата происходит медленнее, чем изменение фактора. Иначе говоря, вариация результата меньше вариации фактора.
Практически в каждом отдельном случае фактическая величина y складывается из двух слагаемых:
где 
– фактическое значение результативного признака; 
- теоретическое значение результативного признака, найденное из уравнения регрессии;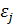 
- случайная величина, характеризующая отклонение реального значения результативного признака от теоретического.
Случайная величина 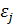, или возмущение, включает влияние неучтенных факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: выбором модели, выборочным характером исходных данных, особенностями измерения переменных.
Этапы регрессионного анализа.
1. Выбор вида модели.
В качестве модели выбрано уравнение парной линейной регрессии вида:
2. Построение линейной регрессии.
Построение линейной регрессии сводится к оценке ее параметров 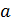и .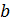
Классический подход к оцениванию параметров линей ной регрессии основан на методе наименьших квадратов (МНК).
Этот метод позволяет получить такие оценки параметров 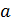и 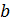, при которых сумма квадратов отклонений фактических (наблюдаемых) хначений результативного признака y от расчетных (теоретических) минимальна:
Т.е. из всего множества линий, проходящих через корреляционное поле наблюдений, линия регрессии выбирается так, чтобы сумма квадратов расстояний по вертикали между точками-наблюдениями и этой линией была бы минимальной.
Для того, чтобы найти минимум функционала S, необходимо вычислить частные производные по каждому коэффициенту регрессии и приравнять их к нулю.
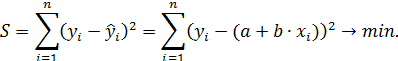
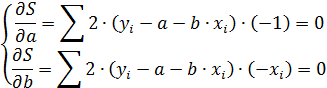
После алгебраических преобразований получим следующую систему нормальных уравнений для оценки параметров 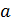и :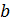
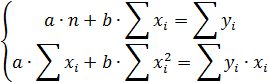
Решение полученной системы дает искомые оценки параметров.
3. Оценка значимости коэффициентов (параметров) регрессии.
Проверка коэффициентов регрессии на значимость дает возможность выявить те независимые переменные
, которые слабо влияют на результирующую переменную y. Коэффициент называется значимым, если он в статистическом смысле отличен от нуля. И наоборот: коэффициент регрессии является незначимым, если он в статистическом смысле близок к нулю. Те переменные 
, входящие в уравнение регрессии, у которых соответствующие коэффициенты являются незначимыми, можно исключить из уравнения.
Проверку на значимость коэффициентов регрессии осуществляют согласно теории статистических гипотез по статистическому критерию Стьюдента.
Как известно, проверка любой гипотезы (в данном случае проверка на значимость) связана с последовательным выполнением следующих этапов.
1) формулируется нулевая и альтернативная гипотеза (H0 и H1):
H0: 
- коэффициент 
- незначим;
H1: 
- коэффициент - значим.
2) выбирается критерий проверки (в данном случае – критерий Стьюдента) и уровень значимости 
3) определяется расчетное значение статистики Стьюдента (t – статистика).
Для этого по каждому из параметров определяется его стандартная ошибка: 
и 
.
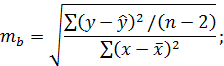
Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при (
степенях свободы и применяется для проверки статистической значимости коэффициента регрессии и для расчета его доверительных интервалов.
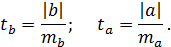
4) определяется критическое (табличное) значение t – распределения для заданного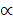 
/2 и числа степеней свободы f = n-2.
5) сравниваются tр c tкр: гипотеза Н0 отвергается, если tр > tкр, то есть соответствующий коэффициент регрессии значим, в противном случае коэффициент регрессии незначим и соответствующая переменная в уравнение регрессии не включается.
Доверительный интервал для коэффициентов регрессии определяется как 
; 
.
4. Проверка качества (адекватности) уравнения регрессии.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера.
Непосредственно расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной y от среднего значения 
на две части – «объясненную» (уравнением регрессии) и «остаточную» («необъясненную» уравнением регрессии):
| Общая сумма квадратов отклонений | Сумма квадратов отклонений, объясненная регрессией | Остаточная сумма квадратов отклонений |
Общая сумма квадратов отклонений индивидуальных значений результативного признака y от среднего значения вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси Ох и 
. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если же прочие факторы не влияют на результат, то y связан с функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией или факторная сумма квадратов, совпадает с общей суммой квадратов.
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс, как обусловленный влиянием фактора , так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака
приходится на объясненную вариацию.
Для оценки качества подбора линейной регрессии вычисляют коэффициент детерминации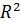 
:
или
Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии результативного признака. Чем ближе 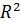к единице, тем выше качество модели. Соответственно, величина (1-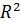) характеризует долю дисперсии 
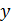, вызванную влиянием остальных, неучтенных в модели, факторов.
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию ϭ2 на одну степень свободы и вытекающую из нее стандартную ошибку ϭ
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии на одну степень свободы, получим величину 
:
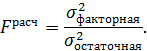
F-статистика используется для проверки нулевой гипотезы
Расчетное значение F-статистики сравнивается с табличным. Табличное значение F-статистики – это максимальная величина отношений дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Если 
, то нулевая гипотеза отклоняется (вероятность нулевой гипотезы ниже заданного уровня (например, 5%)), и делается вывод о значимости (существенности) уравнения регрессии (связь доказана). В противном случае уравнение регрессии считается статистически незначимым.
Величина F-критерия связана с коэффициентом детерминации 
5. Экономический анализ уравнения регрессии.
По группе предприятий, выпускающих продукцию одинакового вида, исследуется функция издержек 
. Данные наблюдений по 7 предприятиям представлены в таблице.
| № п/п | Выпуск продукции, тыс.ед. ()
| Затраты на произ-водство, млн.руб. ()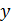
|
В результате регрессионного анализа получено уравнение регрессии:
В соответствии с полученным уравнением имеется прямая линейная связь между издержками и объемом выпускаемой продукции. При увеличении объема выпуска на 1 тыс. ед. затраты на производство в среднем возрастают на 36,84 млн. руб. Величина параметра 
в данном случае не имеет экономического смысла.
Оценка значимости параметров регрессии показала, что коэффициент регрессии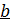 
значим (16,73>2,57), а свободный член – незначим (0,78<2,57) и его можно исключить из уравнения регрессии.
(Примечание. 
).
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 
.
По данным нашего примера величина линейного коэффициента корреляции составила
что означает наличие очень тесной зависимости затрат на производство от величины объема выпущенной продукции.
Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. Между признаками может оказаться достаточно тесная нелинейная связь.
Линейный коэффициент корреляции логически связан с коэффициентом регрессии :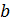
где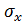
- среднее квадратическое отклонение фактора ; 
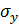- среднее квадратическое отклонение фактора .
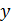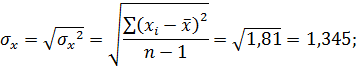
Его величина выступает в качестве стандартизированного коэффициента регрессии и характеризует среднее в сигмах (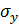) изменение результата с изменением фактора на одну сигму (
).
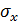В нашем примере при увеличении объема выпуска на 1,345 тыс. единиц затраты на производство в среднем возрастают на 50 млн. руб.
Показателем силы связи, выраженным в процентах является коэффициент эластичности. При линейной связи признаков и 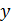средний коэффициент эластичности в целом по совокупности определяется как
В нашем примере коэффициент эластичности 
=1,05%, т.е. при возрастании объема выпуска на 1% затраты на производство возрастают на 1,05%.
Проверка качества полученного уравнения регрессии показала, что коэффициент детерминации 
. Таким образом, уравнением регрессии объясняется 98,2% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,8% его дисперсии. Уравнение регрессии адекватно описывает изучаемый процесс.
Оценка значимости уравнения регрессии с помощью F-критерия Фишера дала возможность сделать вывод о значимости уравнения регрессии.
(
).
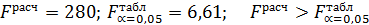В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение 
как точечный прогноз путем подстановки в уравнение регрессии соответствующего значения . Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки , т.е.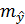 
, и соответственно получают интервальную оценку прогнозного значения 
:
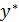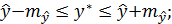
В нашем примере при 
доверительный интервал с вероятностью 95% составит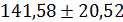 
, т.е. 
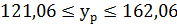. Интервал достаточно широк, прежде всего, за счет малого объема наблюдений. На графике границы доверительного интервала для представляют собой гиперболы, расположенные по обе стороны от линии регрессии, которые определяют 95%-ый доверительный интервал для среднего значения у при заданном значении .
| <== предыдущая страница | | | следующая страница ==> |
| | |
Дата добавления: 2014-03-11; просмотров: 1163; Нарушение авторских прав
Мы поможем в написании ваших работ!