Скорость упругой волны

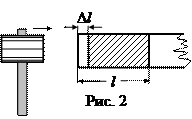Для нахождения скорости распространения волны в упругой среде рассмотрим простейший случай передачи деформации через упругий стержень. В течение короткого промежутка времени Dt ударом молотка сообщим стержню некоторый импульс (рис. 2). За это время точки торца стержня сместятся на некоторое расстояние Dl. Возникшая деформация будет перемещаться от точки к точке, и по стержню побежит волна сжатия. К концу промежутка Dt сжатие охватит участок стержня длиной l.

Отношение 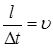представляет собой скорость распространения волны сжатия по стержню.

К концу промежутка Dt все частицы участка стержня длины l будут двигаться со скоростью u = 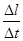, вправо. Поскольку вначале этого промежутка частицы были неподвижны, то приращение импульса стержня будет равно ти, где т – масса участка l. Если площадь поперечного сечения стержня S, плотность материала r, то т = rSl. По второму закону Ньютона приращение импульса тела равно импульсу внешней силы FDt, поэтому:

FDt =rSlu. (5)

Сила F, сжимающая стержень, связана с деформацией Dl сжатого участка l законом Гука

F=ЕS 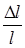, (6)

где Е — модуль Юнга. Исключив из уравнений (5) и (6) силу F и преобразовав, получим:

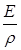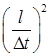= = u².

Отсюда скорость распространения волны сжатия в упругом стержне равна

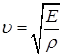. (7)

Для стали Е » 1,96×10¹¹ 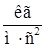, плотность r = 7,8×10³ кг/м³, поэтому u = 5000 м/с.

В случае деформации сдвига в упругой среде возникают поперечные волны, скорость которых

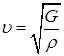. (8)

где G – модуль сдвига.

Дата добавления: 2014-07-19; просмотров: 219; Нарушение авторских прав

Мы поможем в написании ваших работ!