
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОРГАНИЗАЦИЯ ОБУЧЕНИЯ. УРОК ПО МАТЕМАТИКЕ
Последние десятилетия XX века ознаменовались стремительным ростом численности населения Земли (уже сейчас оно превышает 6 млрд. чел.) и его научно-технической вооруженностью. Все это создало невиданное до сего времени активное антропогенное воздействие на биосферу, масштабы антропогенных и естественных факторов влияния на среду стали сопоставимыми. В этом сбылось предсказание В.И. Вернадского, что человеческая деятельность превратилась в геологический фактор. Геологические процессы происходят неизмеримо медленнее, чем мощная строительная деятельность последних двухсот лет.
Строительство — один из самых мощных видов производственной деятельности XX века, превратилось в природообразующий фактор. Изменяемая при строительстве геологическая среда оказывает значительное влияние на протекание процессов в сложившемся круговороте вещества, энергии и информации в биосфере, часто дестабилизируя круговоротные процессы. Повсеместное загрязнение окружающей среды разнообразными веществами представляет серьезную опасность для нынешнего и будущего поколений человека на Земле. Налицо наличие глобального экологического кризиса. Выходом из него для человека является сохранение природной среды.
Современная кризисная экологическая ситуация в своем разрешении требует экологизации многих сфер человеческой деятельности и, в частности, строительства, как чрезвычайно мощного фактора воздействия на природную среду. Необходимо учитывать, что строительство свое воздействие будет наращивать в связи с ростом общей численности населения Земли и с нарастающей урбанизацией (уже сейчас почти 60 % населения живет в городах). Кроме того, проявилась тенденция к созданию мегаполисов и промышленных зон большой территории. Строительная экспансия не обязательно связана с новыми строительством и освоением территорий, но все больше будет направлена на реконструкцию имеющихся поселений и промышленных комплексов и активное освоение подземного пространства. При этом существенно возрастают роль инженера-геолога и инженера-строителя, обладающего геологическими знаниями. В условиях реконструкции существующих сооружений им придется использовать уже измененную геологическую среду, а также проектировать и возводить («переделывать») здания в условиях влияния других зданий при имеющейся плотной городской застройке. При этом нарастают требования по обеспечению безопасности и надежности сооружений даже при мощных природных и техногенных чрезвычайных ситуациях, так как при росте численности населения Земли все чаще надо использовать под строительство сложные в геолого-климатическом отношении территории. Для жизни человека и работе в комфортных условиях необходимо улучшать качество зданий и сооружений. Главнейшим требованием на ближайшую перспективу остается снижение техногенного натиска на биосферу, устранение загрязнений и т. д.
Ставшее классическим определение Е.М. Сергеева трактует инженерную геологию как науку о рациональном использовании и охране геологической среды от вредных для человека и природы процессов и явлений. Это определение высказано более 20 лет тому назад и во многом предопределило экологизацию самой «инженерной» из всех геологических дисциплин науки. При этом вся предыдущая история инженерной геологии имела вполне определенные экологические корни. Даже и возникновение инженерной геологии обусловлено вполне экологическим фактором – требованиями обеспечения строителей необходимыми для расчетов фундаментов сведениями о прочности и деформируемости грунтов. Поэтому встречающееся иногда расхожее определение инженерной геологии как геологии на службе у строителей, в общем-то, достаточно точное. Строительство, являясь чрезвычайно важным экологическим фактором, предопределило инженерную геологию как науку экологического цикла.
Под «строительной системой» мы понимаем здания, сооружения и их комплексы с инфраструктурой инженерных сетей, обеспечивающих их функционирование, а также сосредоточенные в них технологии. Устойчивость строительной системы, ее надежность и безопасность для человека определяется в итоге качеством взаимодействия системы с геологической средой. Изменяемость геологической среды – это геологические процессы, которые усложняют задачи строителей и «провоцируют» свое дальнейшее развитие уже под воздействием созданной строительной системы.
Экологические аспекты взаимодействия строительства и геологической среды приводят к необходимости комплексного рассмотрения системы «сооружение – окружающая среда», что в значительной мере и предопределило формулирование экологической проблематики в геологии. Е.А. Козловский в 1989 г. назвал это новое научное направление геоэкологией. В разработках К.И. Сычева говорится, что предметом геоэкологии являются знания не только о состоянии геологической среды и всех ее компонентов в отдельности, но и происходящих в них процессах.
Геоэкология как междисциплинарная наука рассматривает человека фактором развития и в то же время объектом защиты его от различных геосферных процессов.
Глобальная проблема охраны природной среды затрагивает как все человечество в целом, так и все страны и народы, и может быть решена лишь коллективным разумом и при объединении усилий всех людей на Земле. Это связано с тем, что природные ресурсы планеты (атмосфера. гидросфера, флора, фауна) не могут быть разделены государственными границами; этих границ не признают и многие загрязнения.
7.8. Управление охраной природной среды.
Мониторинг и рекультивация земель
В строительном деле важнейшей задачей является прогноз возможных нарушений природной среды и выработка рекомендаций по их устранению, т. е. нужна система управления природными процессами, сопровождающими строительство.
Важнейшим управляющим инструментом является нормативно правовой механизм, регламентирующий в данном случае экологические аспекты производственной, в том числе строительной деятельности. Следует отметить, что в инженерно-геологические изыскания входит как составной элемент – обязательное выполнение требования по охране и рекультивации среды (рис. 100).

Рис. 100. Отработанный карьер, превращенный
в зону отдыха

Основы мониторинга. В последние годы деятельность человека по охране природной среды резко активизировалась, появился мониторинг. Мониторинг – это система наблюдений, оценки и прогноза состояния окружающей человека природной среды.
Охрана земной коры складывается из трех основных проблем: охраны геологической среды; охраны почв; борьбы с инженерно-геологическими процессами.
|
Охрана почв. Поверхностный почвенный слой земли играет важную роль в протекании жизненных процессов, являясь источником получения продуктов питания. За последнее пятидесятилетие на Земле потеряна пахотная площадь размером с полуостров Индостан, многие почвы теряют плодородие. Правовая охрана почв представляет совокупность законодательных мероприятий, направленных на эффективное и рациональное их использование, на всемерное сохранение и защиту от вредных воздействий. Перед строительством почвенный слой должен быть снят и размещен на другой территории. Строительство и эксплуатация объектов способствуют возникновению инженерно-геологических процессов (оползни, обвалы, провалы земной поверхности над подземными выработками, подтопление водой объектов и т.д.). Поэтому требуется разработка способов защиты территорий исходя из местных геологических условий и природной обстановки (рис. 102).
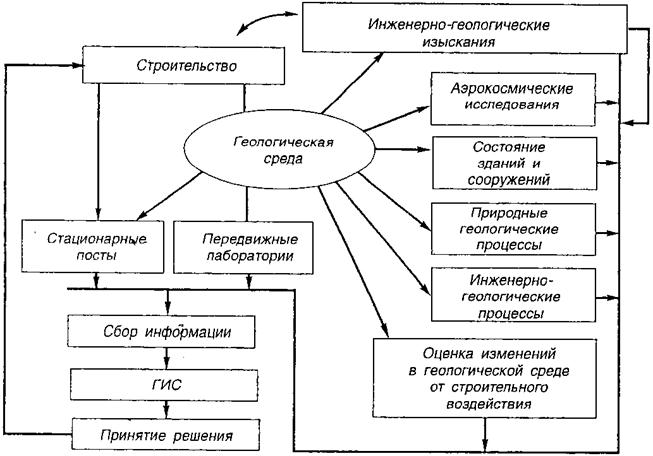
Рис. 102. Функциональная схема геоинформационной системы оценки влияния строительства на геологическую среду
Рекультивация земель – это всестороннее восстановление поверхности земной коры, нарушенной в процессе техногенной деятельности человека. Она бывает двух видов: горно-техническая и биологическая.
Горно-техническая рекультивация – это приведение нарушенной поверхности земли в порядок. Работа начинается с планировки территории и покрытия слоем почвы (до 15 см). Затем создается дерновый слой, хорошо укрепляя поверхность земли, особенно склоны рельефа. При необходимости грунтовые воды регулируются дренажами. Принимаются меры по предотвращению инженерно-геологических процессов.
Биологическая рекультивация предусматривает освоение территории под жилую застройку или создание зон отдыха. После планировки поверхность покрывают почвой с посадкой деревьев, кустарников и посевом сельхозкультур. В местах отработанных карьеров возможно создание водоемов (см. рис. 100).
Задачи строителей по охране природной среды при производстве работ и эксплуатации объектов сводятся к тому, чтобы всегда находить средства и технические возможности для исключению отрицательных воздействий на природную среду.
Строители должны относиться к охране природы, как к важнейшей своей служебной обязанности, быть организатором и руководителем всех природоохранительных работ. При проектировании следует оценивать степень будущего нарушения природы. Иногда от строительства необходимо даже отказаться. Нежелательно занимать земли, пригодные для сельскою хозяйства, а целесообразно использовать непригодные или малопригодные. В период строительства необходимо особое внимание уделять сохранению почв. Грунты, образуемые при вскрытии котлованов, следует вовлекать в сферу строительства (отсыпка насыпей, планировка территорий и т. д.) и не делать отвалов. Не менее важным мероприятием по охране природы при строительстве и эксплуатации объекта является борьба с запылением воздуха, загрязнением водоемов и зеленых массивов, против усиления эрозии, отравления почв.
ОРГАНИЗАЦИЯ ОБУЧЕНИЯ. УРОК ПО МАТЕМАТИКЕ.
ВОПРОСЫ:
1. Оценка знаний.
2. ТИПЫ (ВИДЫ) УРОКОВ ПО МАТЕМАТИКЕ
3. САМОСТОЯТЕЛЬНАЯ РАБОТА ШКОЛЬНИКОВ
4. ТРЕБОВАНИЯ К СОВРЕМЕННОМУ УРОКУ МАТЕМАТИКИ
5. ОЦЕНКА ЗНАНИЙ И УМЕНИЙ УЧАЩИХСЯ
6. ФАКУЛЬТАТИВНЫЕ ЗАНЯТИЯ
7. ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ
8. ПЛАНИРОВАНИЕ РАБОТЫ И ПОДГОТОВКА УЧИТЕЛЯ К УРОКУ
В основе организации учебного процесса лежит классно-урочная система, которая сложилась более 300 лет назад. В этой системе урок является основным звеном, а к вспомогательным звеньям относят домашнюю работу школьника, факультативные занятия, внеклассную работу, индивидуальную и групповую работу с отстающими школьниками.
Дидактика выделяет следующие структурные элементы урока:
1) изучение нового материала;
2) закрепление нового материала;
3) решение задач или упражнений;
4) повторение ранее изученного материала;
5) проверка выполнения домашней работы учащимися;
6) постановка нового домашнего задания;
7) контроль и учет знаний, навыков и умений учащихся.
Все эти элементы одновременно редко встречаются на уроке, однако, используя их, можно составить любой урок.
Остановимся на некоторых структурных элементах урока.
Познание материала новой темы на уроке должно осуществляться в процессе активного учения школьников при интенсивном использовании их самостоятельного мышления. Сообщение готовых знаний нужно ограничить необходимым минимумом, а функцию преподавания свести в основном к организации и управлению активным, развивающим учением. К этому нужно стремиться постоянно, начиная с первого дня работы в школе, стремясь к поиску или разработке материалов, позволяющих высокоэффективным современное преподавание математики.
Необходимость закрепления основана на психологической закономерности процесса усвоения нового знания или способа действия. В ходе урока познание нового материала часто естественно переходит в его закрепление, а иногда и чередуется с ним. При программированном обучении закрепление обычно включается в саму программу. При проблемном обучении закрепление осуществляется в процессе проверки и обсуждения самостоятельного решения проблемы и его результата. Аналогично происходит и в процессе самостоятельного познания нового материала. При лекционном изложении закреплению воспроизведением подвергаются лишь более трудные части темы.
К закреплению материала на данном уроке относят также и первое применение его к решению задач. Уже здесь надо практиковать самостоятельное решение, которое является основным методом обучения на тренировочных уроках, полностью отводимых для решения задач с целью выработки прочных навыков, умения применять теорию.
Естественное свойство человеческой психики постепенно забывать то, что было известно, требует регулярного и периодического повторения ранее изученного. В каждом классе параллельно с изучением нового материала проводится систематическое повторение основного материала. Этому уделяется особое внимание в выпускных классах, где в конце учебного года на повторение и подготовку к экзаменам отводится еще дополнительное учебное время. В конце большой темы (раздела) рекомендуется проводить урок обобщенного повторения. При этом повторяют не только главное из теории, но и решение основных видов упражнений или задач. При большом объеме нового материала не рекомендуется включать в домашнее задание повторение ранее изученного. Повторение должно быть творческим и разнообразным и вызывать интерес у школьников. Оно должно обобщать, систематизировать и углублять изученные ранее знания, открывать их новые качества, обеспечивать прочность усвоения.
На каждом уроке преследуется несколько дидактических целей, т.е целей, которые формируют математические знания, умения и навыки. Однако среди этих целей одна является главной. В зависимости от главной дидактической цели выделяют основные типы уроков по математике:
1) урок первоначального усвоения новых знаний;
2) урок формирования умений и навыков в применении знаний;
3) урок итогового закрепления знаний через обобщающее повторение;
4) урок итогового контроля и учета знаний и навыков.
По математике примерно половину всех уроков составляют уроки первоначального усвоения знаний. Эти уроки делятся на два вида, которые условно можно назвать «урок новых знаний» и «комбинированный урок».
Комбинированный урок по математике обязательно содержит проверку правильности и сознательности выполнения домашнего задания и обычно с этого начинается. Учитель проверяет решение домашних задач (упражнений), а также усвоение материала прошлого урока и повторяемой темы путем индивидуальных заданий отдельным ученикам и фронтального опроса. Затем переходят к изучению нового материала, его закреплению и, наконец, к постановке домашнего задания по новой теме и по повторению ранее изученного. Достаточно полная структура комбинированного урока является его достоинством, но с ней связан и основной, весьма серьезный его недостаток: на таком уроке часто не хватает времени, причем от этого страдает, как правило, основная цель урока – первоначальное усвоение нового материала. Затянувшиеся проверка домашнего задания и опрос учащихся нередко вынуждают учителя воспользоваться традиционным методом сообщения готовых знаний, закрепление провести в спешке, в результате чего многие учащиеся не усвоят или слабо усвоят новый материал и окажутся, не готовы к самостоятельному решению домашних упражнений. К комбинированному уроку нужно прибегать лишь тогда, когда материал новой темы (теоретическая часть и упражнения, которые следует решить на этом же уроке) мал по объему и не вызовет затруднений в данном классе.
Поэтому большинство уроков по первоначальному усвоению новой темы строится по схеме урока новых знаний, отличной от схемы комбинированного урока. Урок новых знаний сразу нацелен на изучение и закрепление материала новой темы и начинается с краткого опроса, направленного лишь на подготовку учащихся к работе над новым материалом и к его усвоению на данном уроке. После того как учащиеся вспомнили необходимые формулировки и факты, сразу приступают к изучению нового материала, стремясь применять при этом современные методы обучения. Даже если при этом потребуется несколько больше времени, чем при сообщении готовых знаний, то такая дополнительная затрата окупается достигаемыми результатами. В активном, развивающем учении проходит как познание нового материала, так и закрепление его с применением, в частности, самостоятельного решение упражнений учащимися. В итоге все учащиеся класса будут достаточно подготовлены к выполнению домашнего задания.
Уроки формирования умений и навыков в применении знаний, которые еще называют тренировочными уроками, имеют столь же широкое распространение в обучении математике, как и уроки новых знаний. На каждом тренировочном уроке большинство работ должно выполняться каждым учеником самостоятельно, и с этой целью задания для самостоятельной работы составляются в нескольких вариантах. Теоретический материал на этих уроках также должен «работать» при обосновании всех шагов решения и обеспечивать выработку сознательных умений и навыков, углубляя при этом понимание учащимися теоретических вопросов математики. Тренировочный урок, который полностью посвящен самостоятельному решению задач учащимися, называют уроком самостоятельной работы. Важность таких уроков следует из того, что умение решать задачи формируется в основном на тренировочных уроках, а без такого умения нет знания математики.
К урокам итогового контроля и учета знаний и умений по математике относят, прежде всего, уроки письменных контрольных работ. Задания такой работы даются в классе не менее чем в четырех вариантах. Эти задания содержатся в» Дидактических материалах». Там же имеются и наборы самостоятельных работ. По каждой теме (разделу) курса проводится итоговая контрольная работа, а по отдельным частям темы проводятся контрольные работы, рассчитанные либо на один урок, либо примерно на 20 минут. Эти краткосрочные контрольные работы рассчитаны на своевременное выявление и устранение пробелов по части темы, что позволяет подготовить учащихся класса к успешному выполнению итоговой контрольной работы. На следующем уроке после проведения контрольной работы нужно провести краткий анализ контрольной работы, отметить основные ошибки и недочеты, дать отдельным ученикам задания по работе над ошибками дома.
Иногда проводятся уроки устного контроля и учета знаний и умений в конце четверти или зачетные уроки по определенной теме. Однако основу устного контроля и учета знаний и умений составляет текущий учет, осуществляемый по возможности на каждом уроке и завершающийся выставлением оценок. Каждую оценку нужно объявить перед классом и мотивировать, надо использовать ее воспитательное значение. Для накопления текущих оценок следует стремиться опросить возможно большее число учащихся на каждом уроке.
Самостоятельная работа школьников – важнейший элемент в обучении математике, позволяющий систематично и прочно усваивать изучаемый материал, развивать творческую составляющую обучения, а также воспитывать у учащихся волевые качества, стремление к достижению цели и др.
В дидактике существуют различные классификации самостоятельных работ, но наиболее известным являются:
1) По степени самостоятельности учащихся.
2) По степени индивидуализации.
3) По дидактическим целям.
4) По источнику знаний.
По степени самостоятельности П.И. Пикадистый различает следующие виды самостоятельных работ:
1) Воспроизводящие самостоятельные работы по образцу.
2) Реконструктивно-вариативные.
3) Эвристические.
4) Творческие (исследовательские).
Самостоятельные работы первого вида позволяют овладеть основными умениями и знаниями и выполняются по жесткой схеме путем последовательных выполнений строго определенных действий. Эти работы направлены на овладение учебным материалом, но не обучают школьников творческой деятельности. Как правило, эти самостоятельные работы состоят из упражнений по образцам и алгоритмам.
Реконструктивно-вариативные самостоятельные работы составляются в нескольких вариантах и наряду со стандартными заданиями, или заданиями, выполняемыми по образцу, содержат задания более высокого уровня самостоятельности и задания, выполнение которых требует нестандартного подхода, сообразительности.
Творческие самостоятельные работы – это такие работы, при выполнении которых, ученик открывает для себя новое. [1] Они позволяют формировать у учащихся интерес к математике, а также развивают математическое мышление.
К творческим работам относят [1]:
1) решение задачи или доказательство теоремы нестандартным, новым для ученика способом;
2) решение задачи несколькими способами;
3) составление задач самими учениками;
4) написание математических сочинений;
5) составление и выступление с докладом.
По дидактическим целям различают следующие виды самостоятельных работ:
1) работы, способствующие формированию математических понятий;
2) работы, направленные на закрепление нового материала;
3) работы, позволяющие формировать умения применять полученные знания при решении задач.
По источнику знаний самостоятельные работы делятся на следующие виды [1]:
1) работа с учебником;
2) работа со справочной или дополнительной литературой;
3) решение и составление задач;
4) сочинения и доклады.
Самообразование невозможно без самостоятельной работы и без умения работать с книгой. Поэтому, начиная с младших классов, необходимо систематически и целенаправленно учить школьников различным приемам получения информации с помощью книги, учебника.
Если тема урока в значительной степени знакома учащимся и не может вызвать у них больших затруднений, то учитель дает задание самостоятельно проработать ее на уроке по учебнику без предварительного изложения и объяснения. В средних классах новый материал урока разбивается на несколько частей, и каждая часть проверяется отдельно путем опроса после проработки ее по учебнику. В старших классах можно дать для проработки сразу всю тему урока, но при проверке результатов последовательно вызвать несколько учеников. Остальные учащиеся следят за ответом, подмечая неточности, пропущенные места или ошибки и делают свои замечания и дополнения. Во время выполнения самостоятельной работы с тестом, учитель наблюдает, как учащиеся пользуются рациональными способами работы, с которыми необходимо знакомить учащихся, начиная с младших классов и которые включают в себя такие моменты:
1) работа с определением;
2) чтение текста и выделение главного;
3) чтение текста и составление плана ответа;
4) пересказ прочитанного по плану;
5) ответы на вопросы в конце параграфа или раздела.
Во время проведения самостоятельного решения задач учитель оказывает индивидуальную помощь слабым ученикам, а также дает задания сильным. При необходимости кратко обсуждает с классом результат, отдельные этапы решения, его идею, план.
Самостоятельная работа школьников – основной метод их работы над учебным материалом при выполнении домашней работы. От успеха этой работы в значительной степени зависит успех всего обучения. Поэтому очень важно учителю обращать внимание на объем и структуру домашнего задания, чтобы оно с одной стороны было посильно каждому ученику и в тоже время способствовало повторению и закреплению приобретенных на уроке знаний и навыков. В этой связи учителю следует стремиться к дифференциации домашнего задания в зависимости от успехов и способностей ученика.
Эти требования реализуются студентом, прежде всего, при разработке модели современного урока в виде плана-конспекта урока, который подобно сценарию определяет деятельность учителя и учащихся в любой момент урока. При разработке такого плана-конспекта (для краткости его будем называть в дальнейшем "план") необходимо:
1. В соответствии с календарным (тематическим) планом и программой по математике определить тему урока и количество уроков, отводимых на изучение материала соответствующего пункта учебника.
2. Внимательно прочитать весь материал пункта учебника, ознакомиться с упражнениями (задачами, вопросами), продумать их решения.
3. Прочитать соответствующий пункт методического пособия для учителя, творчески использовать содержащиеся там рекомендации, дополнительные упражнения и варианты самостоятельной работы (если она предусмотрена на данном уроке) из книги “Дидактические материалы по …”.
4. Распределить материал данного пункта учебника по отводимым на данный пункт урокам. Продумать и учесть связи данного урока с предыдущими и последующими уроками.
5. Сформулировать цели урока: главную дидактическую, а также – развивающую и воспитательную (конкретно).
6. Определить оборудование урока: наглядные пособия, технические средства обучения, дидактические материалы, измерительные и чертежные инструменты. При изложении хода урока указать, где и как это оборудование будет использовано.
7. Целесообразно выбрать тип, вид урока. Если изучается новый материал, то с учетом его объема и характера выбрать урок новых знаний или комбинированный урок.
8. В соответствии с типом, видом урока наметить его структуру, этапы урока, их последовательность, ориентировочно указать время, отводимое на каждый структурный элемент урока.
9. Определить методы обучения, которые целесообразно применить на данном уроке, выделив среди них главный. Этап урока, посвященный изучению (познанию) нового материала, рекомендуется спланировать с применением преимущественно проблемно-эвристических методов, обеспечивающих поисковое познание, активное учение.
10. В плане урока новых знаний формулируют вопросы (или небольшое практическое задание, устный счет), которые должны подготовить учащихся к изучению новой темы, и сразу переходят к этому изучению. Актуализация опорных знаний осуществляется и на других уроках.
11. На первом этапе комбинированного (и тренировочного) урока планируют проверку выполнения письменного домашнего задания и опрос учащихся по материалу предыдущего урока и по повторению. В плане необходимо указать, что конкретно из домашнего задания и как будет проверено на уроке. Наметить в плане, сколько учащихся будет опрошено на оценку, сформулировать для каждого из них группу вопросов-заданий (или карточки-задания).
12. В плане должны быть вопросы по повторению, включаемые в группы вопросов для отдельных учащихся или во фронтальный опрос класса. Как можно чаще ставить вопрос “Почему?”, отражая его в плане урока.
13. При введении на уроке нового понятия или правила необходимо разработать в плане урока применение конкретно-индуктивного подхода, метода целесообразный задач, а при закреплении нового понятия практиковать составление его родословной, при повторении давать задания на классификацию понятий и другую творческую работу с ними, отражая это в плане.
14. При введении теоремы разработать в плане урока генетический подход к ней, применение лабораторного и других методов, позволяющих учащимся открыть для себя нужную закономерность, отраженную в формулировке теоремы.
15. Применяя проблемный подход, необходимо показать, как будет создана проблемная ситуация и выделена из нее проблема, какое конкретно участие в формулировке и решении проблемы примут учащиеся.
16. При изучении нового материала, доказательстве теоремы, фронтальном решении задачи для активизации процесса познания и учения эффективен метод эвристической беседы. В плане необходимо записать продуманную систему логически последовательных вопросов к классу и ожидаемые ответы учащихся. Сочетать эвристическую беседу с применением аналитических методов (анализа-поиска) при доказательстве или решении.
17. Конкретно указать, какие вопросы по новому материалу при его закреплении на уроке поставит перед классом учитель, какие другие формы закрепления, проверки понимания и усвоения материала учащимися будут применены.
18. Необходимо указать, какие упражнения (задачи) будут решены на уроке фронтально, коллективно и какие самостоятельно по вариантам (их рекомендуется дифференцировать по сложности). Планируя обучение решению задачи нового типа или нестандартной задачи, разработать в плане образец возможного совместного с учащимися аналитического поиска решения. Тренировочные упражнения также даются с решениями.
19. В плане урока новых знаний необходимо указать, что из прошлого домашнего задания и как будет при возможности проверено в заключительной части урока или тетради учащихся будут собраны для проверки.
20. В плане указывается, что задается на дом по новой теме и по повторению. Домашние упражнения (задачи) в плане решаются (полностью или сокращенно), записываются при необходимости замечания по ним для учащихся.
21. Наряду с обязательным домашним заданием, к выполнению которого должны быть подготовлены на уроке все учащиеся класса, включается задача повышенной трудности для любителей математики.
22. В плане указывается, в какой форме будут подведены итоги урока.
23. В целях стимулирования домашней подготовки каждого ученика к каждому уроку систематически проводить на уроках 10-минутные фронтальные письменные опросы класса в двух вариантах и включать их задания в план урока. Целесообразно дифференцировать эти опросы по видам знаний: по формулировкам определений и предложений, по доказательствам, по решению задач (упражнений). Оценки по ним накапливаются в рабочей тетради учителя и в обобщенном виде выставляются в классный журнал.
24. Урок математики должен соответствовать принципам развивающего обучения, идеям педагогики сотрудничества, в нем необходимо творчески использовать опыт передовых педагогов.
25. В плане урока в виде примечания указываются:
а) тип, вид урока, мотивируются возможные отступления от типовой структуры;
б) главный метод данного урока;
в) использованная литература.
Оценка знаний и умений учащихся – одна из главных составляющих учебного процесса в школе.. Однако в этой части учебного процесса с конца 80-х, начала 90-х годов начали накапливаться проблемы, вызванные как объективностью выставления оценки, так и небольшой шкалой отметок. Стало понятно, что действующая пятибалльная система оценки знаний не совсем отвечает требованиям школы. Уже тогда возникла более широкая шкала, когда учителя ставили в «свои» журналы и в дневники оценки 1, 2, 3–, 3, 3+, 4–, 4, 4+, 5–, 5. Такая же ситуация наблюдалась и на вступительных экзаменах в вузы, хотя конечная оценка ставилась по пятибалльной системе. Т.е. десятибалльная система возникла приблизительно еще в те годы.
Еще более эта проблема обострилась в начале 90–х годов, когда начали возникать учебные заведения нового типа, и одна и та же оценка означала совершенно разные уровни знаний в различных средних учебных учреждениях.
Все это привело к тому, что в 2002 году Министерством образования Республики Беларусь была введена десятибалльная система оценки знаний учащихся в учреждениях, обеспечивающих общее среднее и профессионально-техническое образование. Целями этой реформы были:
1) повышение объективности оценки и качества учебной деятельности учащихся через введение абсолютной шкалы оценки знаний и умений;
2) обеспечение социальной защищенности личности ученика;
3) реализация комплексного подхода в оценке учебных достижений учащихся через единство знаний, умений и навыков школьников с учетом индивидуальных свойств личности;
4) создание условий для стимулирования учебной деятельности учащихся;
5) формирование у учащихся объективной самооценки успехов в учебно-познавательной деятельности.
Как известно, учебный процесс является двусторонним и для учителя важно иметь обратную связь, чтобы оценить уровень усвоения знаний и умений учащихся на каждом этапе обучения.
Эта процедура получения прямой и обратной связи о ходе и результатах учебного процесса с использованием разнообразных педагогических приемов, методов измерений и оценки учебных достижений учащихся носит название проверки или контроля знаний и умений учащихся.
Оценка – это процесс оценивания степени соответствия реально достигнутых результатов с планируемыми целями, которые задаются образовательными стандартами и программой по математике.
Отметка – это результат процесса оценивания, выраженный в числах.
Оценка, как неотъемлемая часть учебного процесса, несет в себе определенные функции:
1) она должна способствовать формированию мотивации учебного процесса;
2) она должна развивать ценностное отношение к знаниям;
3) она должна способствовать формированию самостоятельности, самоконтроля, воспитывать положительные моральные качества личности (объективность, честность, настойчивость и др.)
Значение оценки проявляется в необходимости регулярно устанавливать степень достижения целей обучения, уровень усвоения знаний, сформированность навыков и умений, а также уровень развития индивидуальных и личностных свойств ученика.
В процессе оценивания необходимо придерживаться комплексного подхода, а потому оценке подлежат:
1) объем усвоенных знаний, их системность и обобщенность;
2) уровень развития умений и навыков, предусмотренных программой;
3) уровень развития индивидуальных свойств личности учащегося, которые отражают и характеризуют достижения учащегося в учебной деятельности.
Десятибалльная система оценки знаний и умений учащихся включает в себя определенные функции, которые помогают достичь поставленных перед этой системой целей.
Контролирующая функция позволяет на каждом этапе обучения объективно оценить уровень обучения как ученика в отдельности, так и класса в целом, а учителю помогает оптимально определить приемы, методы и средства обучения с учетом индивидуальных особенностей учеников.
Образовательная функция ориентирует учителя на использование разнообразных приемов и методов оценивания, которые активизируют учебную и познавательную деятельность учащихся, и позволяют подчеркнуть положительные достижения каждого ученика в соответствии с его возможностями.
Стимулирующая функция предполагает положительное оценивание результата усвоения материала и процесса его достижения, с учетом индивидуальных качеств и свойств личности, что снимает тревогу за полученную оценку и стимулирует учащегося к достижению более высоких результатов.
Диагностическая функция заключается в анализе учебных достижений каждого ученика, его успехов, недочетов, пробелов в знаниях с последующим исправлением выявленных недостатков. Эта же функция связана с индивидуальным подходом к каждому ученику через использование заданий, соответствующих определенным требованиям к знаниям и умениям и учебной деятельности.
Социальная функция предполагает объективную оценку знаний и умений учащегося с использованием шкалы отметок, что способствует достижению определенного уровня образования.
Как уже отмечалось, в процессе разработки новой системы оценки знаний и умений, была внедрена абсолютная шкала оценки учебных достижений учащихся и соответствующая шкала отметок и уровней. Приведем ее в виде таблицы.
| Уровни | Баллы | Показатели оценки |
| 1.Низкий | Узнавание отдельных объектов изучения программного учебного материала, предъявленных в готовом виде (узнавание математических объектов, их свойств, признаков, математических формул, действий, правил, утверждений, моделей, составленных по условию задачи, других элементов математического знания, а также узнавание отдельных математических объектов в окружающей действительности) | |
| Различение объектов изучения программного учебного материала, предъявленных в готовом виде, и осуществление соответствующих практических действий (различение математических объектов, их свойств, признаков, математических формул, действий, правил, утверждений, моделей, составленных по условию задачи, других элементов математического знания и выделение заданных объектов изучения среди предъявленных и в окружающей действительности). | ||
| 2.Удовле- творительный | Воспроизведение части программного учебного материала по памяти (описание математических объектов, перечисление их свойств и признаков; использование инструментов для измерения геометрических величин; выполнение заданий по образцу в одно-два действия) | |
| Воспроизведение большей части учебного материала по памяти (формулирование в устной или письменной форме свойств и признаков математических объектов, правил, утверждений, выделение при сравнении математических объектов общих и отличительных признаков без их объяснения; использование инструментов для проведения основных геометрических построений; выполнение заданий по образцу) | ||
| 3.Средний | Осознанное воспроизведение значительной части программного учебного материала (описание математических объектов и связей между ними без их обоснования или доказательства, иллюстрация примерами окружающей действительности; решение типовых задач по заданному образцу) | |
| Осознанное воспроизведение в полном объёме программного учебного материала (описание математических объектов и связей между ними с элементами обоснования или доказательства; решение типовых задач по известному алгоритму, проверка результатов решения задач с использованием изученных методов) | ||
| 4.Достаточный | Владение программным учебным материалом в знакомой ситуации (обоснование и доказательство математических утверждений при описании математических объектов с учётом внутрипредметных связей; решение типовых задач с использованием нескольких алгоритмов) | |
| Владение и оперирование программным учебным материалом в знакомой ситуации (развёрнутое описание математических объектов, раскрытие сущности математических понятий, правил, утверждений, доказательство математических утверждений, формулирование выводов, подтверждение примерами использования учебного материала в практической деятельности человека; самостоятельное решение типовых задач с полным их обоснованием) | ||
| 5.Высокий | Оперирование программным учебным материалом в частично изменённой ситуации (уверенное владение и оперирование учебным материалом для выполнения учебных заданий с использованием различных способов, приёмов, методов и учётом внутрипредметных и межпредметных связей) | |
| Свободное оперирование программным учебным материалом, применение знаний и умений в незнакомой ситуации (владение приёмами математического моделирования; самостоятельные действия по описанию, объяснению и преобразованию математических объектов; нахождение рациональных способов решения задач, решение творческих задач) |
Для оценки знаний и умений учащихся применяют следующие основные виды контроля результатов учебной деятельности учащихся: поурочный, тематический, промежуточный, итоговый.
Выбор формы контроля (устная, письменная и их сочетание) зависит от содержания и специфики изучаемого материала, продолжительности учебного времени, отводимого на изучение темы, этапа и планируемых результатов обучения, возрастных и индивидуальных особенностей учащихся.
Поурочный контроль осуществляется в устной и письменной формах или в их сочетании посредством проведения опроса (индивидуального, группового, фронтального) с использованием контрольных вопросов и заданий, содержащихся в учебниках, учебных, учебно-методических пособиях и дидактических материалах, математических диктантов, собеседования, самостоятельных работ и других методов и средств контроля, которые определяются педагогом с учётом возрастных особенностей учащихся в целях получения объективной информации о качестве учебно-познавательной деятельности учащихся и их учебных достижениях.
Тематический контроль осуществляется посредством проведения самостоятельных и контрольных работ, других методов и средств контроля, которые определяются педагогом с учётом возрастных особенностей учащихся в целях получения объективной информации о качестве учебно-познавательной деятельности учащихся и их учебных достижениях.
При оценке результатов учебной деятельности учащихся учитывается характер допущенных ошибок: существенных и несущественных
К категории существенных относятся ошибки, свидетельствующие о том, что учащийся не знает формул, не усвоил математические понятия, правила, утверждения, не умеет оперировать ими и применять к выполнению заданий и решению задач.
К категории несущественных относятся отдельные ошибки вычислительного характера, погрешности в формулировке вопросов, определений, математических утверждений, небрежное выполнение записей, рисунков, графиков, схем, диаграмм, таблиц, а также грамматические ошибки в написании математических терминов.
Контрольная работа, самостоятельная работа, которые проводятся в рамках тематического контроля, должны включать по одному или по два задания в соответствии с показателями оценки результатов учебной деятельности учащихся при осуществлении контроля с использованием десятибалльной шкалы, установленными настоящими Нормами оценки результатов учебной деятельности.
Отметка за выполнение самостоятельных работ, которые проводятся в рамках тематического контроля, контрольных работ выставляется с применением следующих шкал: шкалы, определяющей максимальное количество баллов за каждое задание и шкалы перевода суммарного количества баллов, полученных учащимся за выполнение соответствующей работы, в отметки по десятибалльной системе.
| Шкала 1, определяющая максимальное количество баллов за каждое задание, если самостоятельная или контрольная работа содержит 5 заданий | Шкала 2 перевода суммарного количества баллов, полученных учащимся за выполнение самостоятельной или контрольной работы, которая содержит 5 заданий |
Шкала 1 Шкала 2
| Номер задания | Максимальное количество баллов за выполнение задания |
| Суммарный максимальный балл за выполнение всех заданий: 30 |
| Количество баллов, полученных учащимся | Отметка по десятибалльной шкале оценки результатов учебной деятельности учащихся |
| 3—5 | |
| 6—8 | |
| 9—11 | |
| 12—14 | |
| 15—18 | |
| 19—23 | |
| 24—28 | |
| 29—30 |
Кроме обязательных организационных звеньев процесса обучения, определяемых программой по математике, есть еще дополнительные звенья этого процесса, выбираемые учащимися по желанию. Это – факультативные занятия и внеклассная работа, предназначенные для любителей математики и находящиеся в определенной взаимосвязи с обязательным учебным процессом. Именно эффективная работа на уроке создает достаточное количество любителей математики, позволяющих отбирать наиболее способных в математике учащихся, которые являются основой для проведения успешной работы на факультативных и внеклассных занятиях. Последние расширяют и углубляют знания, полученные на уроках математики, повышают интерес к предмету, способствуют развитию математических способностей, помогают учащимся правильно решить вопрос профориентации.
Введение факультативов тесно связано с идеей дифференцированного обучения, учитывающего индивидуальные склонности и способности учащихся и относится к концу 60-х годов прошлого века, когда при переходе на новые программы по математике, было выделено учебное время для факультативных занятий в 7 – 10–х классах, а также были созданы специальные физико-математические школы и математические классы ( 9 – 10-е) в отдельных школах. В последствии эта идея нашла широкое применение, и были созданы школы и классы с углубленным изучением других предметов. В 90-х годах прошлого столетия начали создаваться школы нового типа – лицеи, гимназии, колледжи. В них идея профильного обучения нашла свое дальнейшее развитие, как в плане углубления изучения отдельных предметов, так и их расширения по списку и по классам, когда углубленное изучение отдельных предметов начинается еще в начальной или базовой школах.
Однако, как показывает практика, углубленное изучение математики целесообразно начинать самое раннее с 8-го класса, а до этого проблему углубленного изучения математики и проблему развития интереса к предмету следует вести через систему факультативов и внеклассной работы.
Но даже если учащиеся и не выбрали изучение математики на более высоком уровне, не следует ограничиваться проведением только уроков. Среди этих учащихся также следует проводить работу по развитию интереса к математике и не только на уроках. Для этого и предусмотрена система факультативов.
Сейчас в республике проведена работа по разработке примерных планов и программ для факультативных занятий, начиная с 5-го класса. В национальном институте образования разработаны такие программы с расчета 1 час в неделю. Приведем пример такой программы.
Авторы назвали этот факультатив «МАТЕМАТИКА ПОСЛЕ УРОКОВ» и он рассчитан для 5-7 классов общеобразовательных учреждений. Как сказано в преамбуле и пояснительной записке: « Дополнительный курс по математике направлен на развитие математических способностей. В ходе его
изучения учащиеся смогут не только познакомиться с логикой высказываний, теорией множеств, научиться решать сюжетно–логические и стратегические задачи, но поработать с головоломками и числовыми ребусами. Данный курс дополняет программу основного курса математики.»
«Предложенные программы факультативных занятий должны рассматриваться как ориентировочные. Учитель может по своему усмотрению менять содержание факультативных занятий, порядок изучения тем, исключать из рассмотрения отдельные темы или сокращать объем материала внутри тем. Распределение часов по темам не дается, что обеспечивает учителю возможность выбора тех тем, которые по каким-либо причинам для него более предпочтительны.»
Приведем содержание данного курса для 5 – 6 классов.
1. В мире чисел
Метрическая система мер. Римские цифры. Мир больших чисел. Старинные меры длины, площади, объема.
2. Восстановление чисел
Задачи на восстановление цифр и чисел в примерах на сложение и вычитание, умножение и деление. Головоломки с цифрами. Числовые ребусы. Магические квадраты.
3. Сюжетные логические задачи
Задачи, решаемые методом исключения с применением таблиц. Истинные и ложные высказывания. Рыцари, лжецы, хитрецы.
4. Стратегические задачи
Взвешивание монет и предметов. Переливание.
Математика в познавательных и развивающих играх. Выигрышные позиции. Симметрия. Анализ с конца. Возможность выбора правильной стратегии игр.
5. Задачи с геометрическим содержанием
Занимательные свойства геометрических фигур. Геометрические иллюзии. Рисование фигур на клетчатой бумаге. Разрезание фигур на равные части. Игры с пентамино. Вымащивание плоскости различными видами многоугольников. Задачи на построение замкнутых самопересекающихся ломаных (уникурсальные кривые). Лабиринты. Неравенство треугольника. Пифагор и теорема Пифагора. Из истории числа π. Длина окружности. Площадь круга. Геометрия в пространстве.
6. Элементы теории множеств
Множества. Элемент множества. Пустое множество. Подмножество. Равенство множеств. Операции над множествами. Решение некоторых задач с помощью теории множеств. Круги Эйлера.
7. Знакомство с теорией чисел
Множество натуральных чисел. Простые и составные числа. Решето Эратосфена. Взаимно простые числа. Признаки делимости на: 2, 3, 4, 5, 9, 10, 11. Четность и нечетность. Последняя цифра. Простейшие диофантовы уравнения.
8. Комбинаторика.
Перечислительная комбинаторика.
Комбинация предметов. Правило умножения. Перестановки. Факториал. Размещения. Сочетания.
Комбинаторные задачи.
Принцип Дирихле. Обобщенный принцип Дирихле. Следствие из принципа Дирихле. Наверняка (или в худшем случае). Принцип Дирихле и делимость. Принцип Дирихле в геометрии. Окраска плоскости и ее частей. Таблицы.
Графы.
Понятие графа. Язык теории графов. Степень вершин. Подсчет числа ребер. Лемма о рукопожатиях. Деревья. Эйлеровы графы.
9. Текстовые задачи.
Натуральные числа.
Задачи для проверки сообразительности и внимательности. Задачи на движение. Задачи на движение по реке. Задачи на части. Задачи на нахождение двух чисел по их сумме и разности.
Дроби.
Вводные задачи. Нахождение части числа и числа по его части. Сложение и вычитание обыкновенных дробей. Умножение и деление обыкновенных дробей. Задачи на бассейны и совместную работу. Задачи, решаемые с конца.
Пропорции.
Задачи на прямую и обратную пропорциональность. Задачи на прямую и обратную пропорциональность трех величин.
Затем приводятся ожидаемые результаты и обширный список литературы.
Аналогично разработана программа факультатива для 7-го класса.
1. Элементы комбинаторики
Основные понятия комбинаторики: множество, подмножество, упорядоченное множество, пустое множество. Факториал числа. Перестановки, размещения, сочетания (с повторением, без повторения). Правила комбинаторного сложения и умножения. Алгоритмы решения комбинаторных задач. Принцип Дирихле. Инвариант. Элементы теории вероятности.
2. Делимость
Делимость с остатком. Инвариант (остаток от деления). Принцип Дирихле и делимость. Метод математической индукции и делимость.
3. Системы счисления
Перевод чисел из десятичной системы счисления в n-ю. Перевод чисел их п-й системы счисления в десятичную. Действия сложения, вычитания, умножения и деления. Приложение записи чисел в различных системах счисления.
4. Теория многочленов.
Разложения на множители, треугольник Паскаля. Деление многочленов, теория Ньютона. Деление многочлена на двучлен по схеме Горнера. Приводимые и неприводимые многочлены. Теорема Безу. Делимость многочлена Р(х) на х – с. Делимость хm – сm на х – с, m – натуральное. Делимость хm – сm на х + с, при m = 2к, к – натуральное. Делимость хm + сm на х + с, при m = 2к + 1. Метод неопределенных коэффициентов в разложении на множители. Применение следствий из теоремы Безу и метода неопределенных коэффициентов при нахождении корней многочленов.
5. Текстовые задачи
Текстовые задачи: на числовые зависимости; на проценты; концентрацию смесей и сплавов; на совместную работу, производительность; на движение; с числом неизвестных большим числа уравнений; на исследование решений.
6. Решение геометрических задач.
Дополнительные сведения о равенстве фигур, третья группа аксиом. Сравнение отрезков и углов. Треугольники, свойства треугольников. Геометрическая арифметика, Рене Декарт. Золотые сечения, Леонардо да Винчи. Площади фигур. Неевклидова геометрия, Лобачевский.
7. Движение на плоскости.
Некоторые виды движений. Движения и положения. Группы симметрии (треугольника, четырехугольника, круга). Магические треугольники и квадраты.
8. Длина окружности и площадь круга.
Длина окружности. Радианная мера дуги и угла. Площадь круга и его частей.
Как видно из программы, данный факультативный курс тесно примыкает к изучаемому материалу на уроках, существенно дополняет этот материал и позволяет учителю достаточно успешно организовать занятия на факультативе с разными целями: образовательной, развивающей, мотивационной, и др.
В заключение отметим, что недопустимо превращение факультативных занятий в практикум по подготовке к сдаче вступительных экзаменов в вуз. Конечно, эта цель также может преследоваться при занятиях на факультативе в старших классах, поскольку разнообразие задач вступительных экзаменов и по количеству и по идеям решений огромно. Но эта цель не должна быть преобладающей. Необходимо показывать применимость математических идей и способов решения задач не только в процессе решения конкурсных заданий, но и их разнообразное применение в других областях математики, решении задач из других наук и т.д. Тогда факультативные занятия будут способствовать успешной сдаче вступительных экзаменов благодаря повышению общей математической культуры учащихся, а не путем прямого «натаскивания» в решении задач вступительных экзаменов.
К дополнительным звеньям процесса обучения относится наряду с факультативными занятиями и внеклассная работа. В данной области накопился богатый опыт учителей, который частично отражен в литературе. Укажем основные формы внеклассной работы по математике:
1) олимпиады;
2) научно-практические конференции школьников (НПКШ);
3) турниры юных математиков (ТЮМ);
4) вечера, дни, недели математики в школе.
Олимпиада, НПКШ, ТЮМ, как формы внеклассной работы, являются итогом этой работы, а результаты выступления школьников – показателем качества этой работы. Олимпиада, НПКШ, ТЮМ – соревнования, которые стимулируют рост учащихся в смысле их математического образования, воспитывают у них математическое мышление, интерес к математике, настойчивость – желание не отстать от тех, кто успешно участвует в этих соревнованиях. Часто именно участие в этих мероприятиях и подготовка к ним побуждает учащихся к самостоятельной работе, вырабатывает умение работать с литературой.
Первые олимпиады для школьников были проведены в 1894 году в Венгрии. В СССР первая олимпиада по математике была проведена в 1934 году в Ленинграде (ныне Санкт-Петербург), а в 1935 – в Москве. В 1967 году была проведена первая Всесоюзная олимпиада по математике в СССР. Первая международная олимпиада была проведена в 1959 году.
История Белорусских олимпиад начинается с года. С 1991 года, после распада СССР, начинается история национальных олимпиад. В 1992 году наша команда принимала участие в международной математической олимпиаде в качестве наблюдателя, а с 1993 года участвует в международных олимпиаде на общих основаниях.
Белорусская математическая олимпиада проходит в 4 этапа:
1 этап – школьные олимпиады, 2 этап – районные олимпиады, 3 этап – областные и Минская городская олимпиады, 4 этап – Республиканская олимпиада, по результатам которой формируется команда для участия в международной математической олимпиаде.
Учителю, который занимается подготовкой школьников к олимпиадам, следует иметь в виду, что в такой работе важна регулярность и знание тем и задач, предлагаемых школьникам на разных этапах.
НПКШ предполагает выступления учащихся с докладами по различным темам, связанных с математикой. Как правило, темы для исследований предлагаются школьникам учителем. Темы для исследований могут подбираться как из разных разделов математики, так и из разных источников. Это может быть обобщение какой-то задачи, либо решение проблемы, поставленной в математической статье и др.
НПКШ проходит в четыре этапа. Первый этап проводится в школе, если работ для проведения конференции достаточно. Лучшие из таких работ рекомендуются для участия на втором (районном) этапе. Затем проходит областной (Минский) этап, на котором лучшие работы рекомендуются для участия на заключительной Республиканской НПКШ. Лучшие работы на каждом этапе награждаются жюри.
ТЮМ проводится по следующей схеме. В сентябре месяце в периодической печати публикуются задачи, рекомендуемые организаторами турнира для решения в данном году. В школах, лицеях, гимназиях формируются команды, состоящие из 4-5 человек, которые начинают решать предложенные задачи. Затем в декабре месяце проводится первый тур. Этот и другие туры проводятся по следующей схеме (на примере трех команд).
| № задачи № команды | |||
| Д | О | Р | |
| Р | Д | О | |
| О | Р | Д |
Здесь обозначения Д – докладчик, О – оппонент, Р – рецензент.
В задачу докладчика входит изложение решения задачи. В задачу рецензента входит рецензия предложенного решения задачи, а в задачу оппонента входит оппонирование, как докладчику, так и рецензенту.
За каждое действие жюри начисляет каждой команде определенное количество баллов и по сумме набранных баллов определяется победитель, который выходит в следующий тур.
Вечера, дни, недели математики в школе проводится по определенному сценарию, который разрабатывается учителями школы и утверждается администрацией. Эти мероприятия включаются в план работы школы, который принимается на педсовете в августе месяце. Существуют различные сценарии таких мероприятий и отражены в литературе или их можно найти в библиотеке.
Однако, как показывает опыт, внеклассную работу по математике по-настоящему, творчески ведут лишь отдельные учителя, а поэтому в целом эта работа не обеспечивает решения стоящих перед ней задач. Именно поэтому сейчас школы начинают привлекать к ведению внеклассной работы преподавателей ВУЗов. Введение факультативных занятий по математике не отменяет внеклассной работы по этому предмету, и долг каждого учителя систематически и увлечено проводить ее.
К началу каждого учебного года учитель составляет календарный тематический план преподавания отдельно по каждой математической дисциплине в тех классах, в которых ему предстоит работать. Нет единой схемы составления такого планирования, но на наш взгляд, в нем должны быть следующие графы: темы и подтемы программного материала, количество учебных часов, даты исполнения, темы для повторения.
Приступая к работе, учитель внимательно изучает объяснительную записку к программе и программу по математике в данном классе. Надо хорошо знать и соответствующий учебник, объем и характер теоретического и задачного материала по каждому программному вопросу. В методических руководствах для учителя математики по каждому предмету и классу дается тематическое и поурочное планирование, содержащее примерную разбивку часов по темам. Учитель может внести небольшие изменения в эту разбивку, учитывая особенности данного класса. Наиболее удобно сначала составить календарный тематический план на первое полугодие, а затем (во время зимних каникул) – и на второе. К началу учебного года учитель получает подробную программу по своему предмету, разработанную методистами Министерства образования РБ, которая после простановки в ней сроков исполнения будет служить календарным тематическим планом.
Подготовка учителя к уроку начинается с формулировки темы предстоящего урока и его цели. Если тема урока сформулирована таким образом, что она вполне определяет и цель урока, то в плане цель отдельно можно не записывать.
Отметим, что в плане должны быть сформулированы три цели урока: дидактическая (обучающая), развивающая, воспитательная.
Дидактическая цель может предусматривать:
1) Обеспечение и контроль понятий, фактов, правил, теорем, входящих в содержание темы урока;
2) Введение и формулировка каких-то понятий (если понятия достаточно сложные и для их введения и определения требуется много времени);
3) Закрепление умений и навыков учебной работы;
4) Формирование представлений, умений и навыков;
5) Закрепление и углубление знаний и умений учащихся;
Развивающая цель может предусматривать:
1) Развитие интеллекта, воли и познавательных интересов;
2) Развитие умения выделять в изучаемом главное, существенное (составление конспекта, плана, формирование умения сравнивать, обобщать);
3) Развитие у учащихся самостоятельности в учении;
4) Развитие у учащихся речи, памяти, интересов, умений преодолевать трудности.
Воспитывающая цель может предусматривать трудовое, профориентационное, нравственное, эстетическое воспитание.
Внимательно прочитав соответствующий текст учебника и ознакомившись с относящимися к нему упражнениями, продумав их решения, учитель обращается к соответствующей методической литературе.
Работая над задачным материалом учебника, учитель составляет примерную схему распределения задач по урокам, отводимым на данный пункт учебника. При этом рекомендуется придерживаться следующей примерной таблицы распределения задачного материала.
| Номер урока Вид материала | ||||
| Теоретический материал | ||||
| Задачи для решения в классе | На закрепление нового материала | |||
| На повторение | ||||
| Для любителей математики | ||||
| Задачи для решения дома | На закрепление нового материала | |||
| На повторение |
| <== предыдущая страница | | | следующая страница ==> |
| Охрана природной среды как общечеловеческая задача | | | Образование запасов в природе и обществе |
Дата добавления: 2014-08-04; просмотров: 983; Нарушение авторских прав

Мы поможем в написании ваших работ!