
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Определение погрешностей
Как отмечалось ранее, любое измерение по шкале отношений, предполагает сравнение неизвестного размера с известным и выражение первого через второе в кратном или дольном отношении. Q/[Q]
Это сравнение происходит под влиянием множества случайных и неслучайных факторов, точный учет которых невозможен, а результат совместного действия непредсказуем, т.е. уравнение измерений по шкале отношений имеет вид:
X= Q/[Q]+h (1),
где η носит случайный характер.
Если при измерениях используется тара, то X=(Q + V)/Q+ h (2),
где V – вес тары.
Из-за случайного характера η отсчет по шкале отношений получается все время разный. Это фундаментальное положение является законом природы. На основании громадного опыта практических измерений может быть сформулировано утверждение, называемое основным постулатом метрологии: отсчет является случайным числом. На этом основана вся метрология. Уравнение (2) является математической моделью измерения по шкале отношений. Отсчет не может быть представлен отдельным числом, его можно описать словами, математическими символами, представить массивом экспериментальных данных, таблицей, графиком, формулой и т.д. При ста измерениях одной и той же величины постоянного размера на цифровом табло измеряемого прибора случайным образом появляются значения xi, представленные в первой графе. Ни одно из чисел в первой графе таблицы, взятое в отдельности, не является отсчетом.
| xi | mi | P(xi) | F(xi) |
| 90,10 90,11 90,12 90,13 90,14 90,15 90,16 90,17 90,18 90,19 90,20 | . . . . . . | 0,01 0,02 0,05 0,1 . . . . . . 0,01 | 0,01 0,03 0,08 0,18 . . . . . . |
Отсчет характеризуется всей совокупностью чисел с учетом того, как часто они появляются. Принимая частость каждого i-го числа за вероятность его появления P(xi), заполним 3-ю графу. В совокупности с 1-ым столбцом, это даст нам распределение вероятности отсчета, представленное в виде таблицы. Графически это выглядит так.
P(xi) 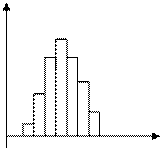
n
Представим в 4-ой графе вероятность того, что на табло измерительного прибора появится число, меньшее или равное тому, которое значится в 1-ой графе. В совокупности с 1-ой графой это даст нам представленную табличную функцию распределения вероятности отсчета.
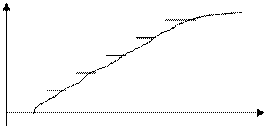 F(Xi)
F(Xi)
Хi
90,1 90,2
Как P(xi), так и F(xi) является исчерпывающим описанием отсчета у измерительных приборов. Описаниями отсчета могут быть также гистограмма и полигон.
 P(Xi)
P(Xi)
Xi
P(xi) и F(xi) служат в теории вероятностей моделями эмпирических законов распределения, полученных из экспериментальных данных методами математической статистики. После проведения процедуры измерения в уравнении (2) остаются неизвестными Q и η. Неслучайная V либо должна быть известна до измерения, либо установится в процессе дополнительных исследований. Слагаемое η является случайным и не может быть известно в принципе, поэтому определить значение измеряемой величины невозможно.
Q = x[Q] – η[Q] – V (3).
Равенство (3) соблюдается точно благодаря тому, что при повторных выполнениях измерительной процедуры случайное изменение 2-го слагаемого в правой части влечет за собой точно такой же изменение 1-го. О таких слагаемых говорят, что они коррелированны.
Разность между коррелированными значениями случайных величин не случайна, но в данном случае не известна. Поэтому строгого решения уравнение (3) не имеет. На практике пользуются приближенным решением, для этого используют результат специального исследования, называемого метрологической аттестацией средств измерений. В ходе этого исследования определяется среднее значение H ≈ η[Q]. Оно не является случайным, поэтому после замены случайного 2-го слагаемого в правой части получится
Q = x[Q] – H – V
В этом выражении результат измерения является случайным значением измеряемой величины
Q = x[Q] – H – V, где x[Q] – показание, [H – V] – поправка
x[Q] = X, Θ = - H – V
В результате получается Qi = xi + Qi. Результат измерения Q подчиняется тому же закону распределения вероятностей, что и показание, но смещенному по оси абсцисс на значение поправки. Следовательно, Qi – результат однократного измерения.
Результат многократного измерения запишется:
n
Qn=1/n S Qi
I=1
Математическая модель измерения по шкале порядка
Q1 + η1>< Q2 + η2
Результат измерения 2-х размеров по шкале порядка является случайным.
Закон распределения вероятностей и их числовых значений
Математический аппарат теории вероятностей широко используется в метрологии. Рассмотрим свойства законов распределения вероятностей.
1. F(x) определяет вероятность того, что отдельный результат, полученный по формуле (2), будет меньше ее аргумента.
2. Так как F(x) ³0, то чем больше x, тем больше вероятность того, что ни один результат, полученный по формуле (2) не превысит этого значения, то есть F(x) – неубывающая функция. При изменении от -¥ до +¥ F(x) меняется тот 0 до 1.
3. Результат, полученный по формуле (2), меньше некоторого x1 c вероятностью F(x1) и меньше другого x2> x1 c вероятностью F(x2). Следовательно, вероятность того, что результат находится в интервале [x1,x2] равна разности F(x) на границах интервала.
P{x1£ x £ x2}= F(x2)-F(x1).
У аналогового измерительного прибора x1 и x2 можно выбрать сколь угодно близкими друг к другу. Следовательно, при x1 ® x2 F(x2)-F(x1) ® 0. Поэтому у аналоговых измерительных приборов вероятность того, что указатель отсчетного устройства остановится в какой-либо конкретной точке шкалы равной 0, т.е. крайние точки можно включать или не включать в интервал.
4. Р(х) связано с функцией F(х) соотношением
Р(х)= F’(х), поэтому Р(х) называют дифференциальной функцией распределения вероятности.
X0
В свою очередь F(x0)=ò P(x)dx
-¥
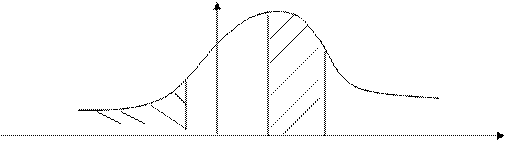 P(x)
P(x)
P{X1 £ X2 £ X3}
F(x0)
X0 X1 X2 X
5. Так как f(x) неубывающая функция, то её произведение не может быть отрицательным P(x) ³ 0.
6. Вероятность того, что отдельный результат, полученный по формуле (2), окажется в интервале [x1, x2] равна площади, ограниченной графиком функции Р(х), осью абсцисс и перпендикулярами к ней на границе интервалов
X2
P{X1 £ X2 £ X3} = ò P(x)dx
X1
При расширении интервала до бесконечности рассматриваемое событие становится достоверным
¥
ò P(x)dx=1
-¥
Описания отсчёта ил результата измерений с помощью законов распределения вероятностей является наиболее полным, но неудобным. Во многих случаях пользуются лишь числовыми характеристиками или моментами. Все они представляют собой средние значения, при чём, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения, то центральными. Важнейшим начальным моментом является первый – среднее значение.
¥
X = ò xp(x)dx
- ¥
Он характеризует математическое ожидание отсчёта при бесконечном повторении процесса измерения по формуле (2). Его часто называют М(х).
Свойства МО:
1. М(а)=а, где а =const, МО неслучайного числа равно самому числу.
2. М(ах)=аМ(х).
3. М(х+y-z)=M(x)+M(y)-M(z).
4. M(xyz)=M(x)*M(y)*M(z)
5. M[x-M(x)]=0, МО отклонения числа от его МО равно 0.
Второй центральный момент – мера рассеивания, иногда его называют дисперсией.
¥
dx2 = (x-x)2 = ò (x-x) p(x)dx
-¥
Свойства дисперсии:
1. D(a)=0.
2. D(ax)=a2D(x).
3. D(x)=M(x2)-M2(x).
Чем больше дисперсия, тем значительнее рассеивание результата, полученного по формуле (2).
P(x)
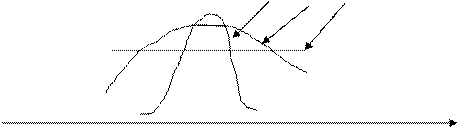
 d12<d22<d32
d12<d22<d32
X
В метрологии мерой рассеивания служит средне квадратичное отклонение, равное квадратному корню из дисперсии.
Находит применение и третий центральный момент:
¥
 (x-x)3 = ò (x-x)3 p(x)dx
(x-x)3 = ò (x-x)3 p(x)dx
-¥
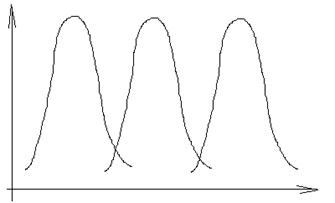
Он является мерой несимметричности m=(x-x)3/dx3
m=0 m<0 m>0
Четвёртый момент является мерой заострённости υ = (x-x)4 / dx4
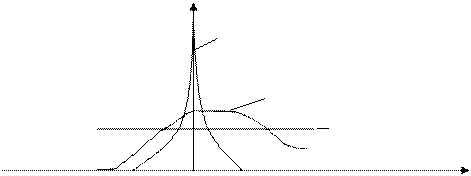 P(x) υ >3
P(x) υ >3
υ=3
υ <3
X
Мерой неоднородности случайного числа является энтропии:
¥
M(x) = ò p(x)logp(x)dx
-¥
Модели эмпирических законов распределения вероятностей отсчёта дифференциальной и интегральной функции распределения вероятностей, как и все моменты, обладает важным качеством: будучи характеристиками случайных чисел, сами они не являются случайными. Описания с их помощью отсчёта было бы удобно, если бы эти характеристики можно было бы получить.
Однако это не возможно, т.к. не возможно повторить процедуру измерения бесконечное число раз.
Поэтому в дальнейшем они будут использованы только в качестве моделей.
| <== предыдущая страница | | | следующая страница ==> |
| Классы точности | | | Влияющий фактор |
Дата добавления: 2014-08-04; просмотров: 376; Нарушение авторских прав

Мы поможем в написании ваших работ!