Определение ориентировки

Весьма распространенной задачей является определение ориентировки кристалла с известной структурой. В этом случае необходимо проиндицировать электронограмму образца, определенным образом ориентированного по отношению к внешней системе координат – ось пучка и плоскость электронограммы. Электронограмма соответствует отражениям от плоскостей зоны, ось которой <u₁u₂u₃>, параллельная электронному пучку, находится из уравнения зональности (нулевая Лауэ-зона):

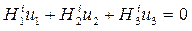(1)

здесь H_jⁱ – индексы i-того узла, принадлежащего данной плоскости обратной решетки.

Выбрав два узла, лежащие на пересекающихся узловых прямых, можем сопоставить соответствующие им межплоскостные расстояния d_H (d/n) с табличными значениями и определить их индексы.

Индицирование не всегда однозначно, так как нескольким совокупностям индексов H_i в общем случае могут отвечать совпадающие или неразличимые в пределах точности измерений значения d_H.

Поэтому более достоверное и однозначное индицирование можно осуществить, сопоставляя экспериментальные и табличные значения d_H и j_HH`. Индексы плоскости обратной решетки, изображенной на электронограмме (u₁u₂u₃), т.е. оси зоны отражающих плоскостей можно найти, зная индексы любой пары узлов H¹ и H² из соотношения (1).

Для высокосимметричных, особенно кубических кристаллов, существует несколько сочетаний индексов H_j, которым соответствует одно и тоже значение d_H и j_{HH`</sub>. Полученные индексы оси зоны определяют один из вариантов, правильно характеризующих ориентировку кристалла. Остальные столь же правильные ориентировки можно получить из уравнения (1) перестановкой и изменением знаков индексов H<sub>j</sub><sup>1</sup> и H<sub>j</sub><sup>2</sup>, сохраняющих те же значения d<sub>H</sub> и j<sub>HH`}. Если ось зоны является в кристалле осью симметрии четвертого порядка, то индицирование одной плоскости обратной решетки (являющейся плоскостью симметрии) позволяет однозначно определить ориентировку кристалла. Если же этого нет, то для однозначного определения ориентировки необходимо привлекать данные об отражении от плоскостей других, не входящих в данную нулевую зону плоскостей. Отражения от этих плоскостей часто имеются на той же электронограмме.

Рассмотрим теперь рефлексы, принадлежащие последующим Лауэ-зонам. Для каждого узла, лежащего в одной из плоскостей, параллельных плоскости (u₁u₂u₃), справедливо соотношение:

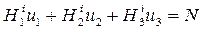(2)

где N - целое число.

Для последовательно расположенных плоскостей ряд значений N определенный. Так, для ГЦК решетки [u₁u₂u₃]=[111] N=0,1,2,3…, а для [u₁u₂u₃]=[110] N=0,2,4… При заданном направлении [u_j] значения N легко получить из уравнения (2), если учесть, что индексы H_jⁱ должны удовлетворять правилам погасания, определяемыми пространственной группой решетки кристалла. Индицирование рефлексов ненулевой Лауэ-зоны позволяет однозначно определить ориентировку кристалла. Плоскости обратной решетки тем ближе одна к другой, чем больше период идентичности вдоль направления [u_j]. В этом случае разделение рефлексов, принадлежащих разным Лауэ-зонам, на электронограмме не четкое. Наоборот Лауэ-зоны легче проявляются, если период идентичности вдоль направления [u_j] небольшой, а плоскости обратной решетки, перпендикулярные этому направлению, густо заполнены узлами. Это обычно бывает, если индексы U_j соответствуют важному направлению. Хорошо выраженные Лауэ-зоны получаются на электронограмме, если важное направление отклоняется на малый угол r от оси пучка. В этом случае рефлексы располагаются так, что центр электронограммы отклонен от следа важного направления на расстояние r. Тогда угол между пучком и этим направлением можно определить из уравнения:

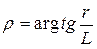
где L – расстояние от образца до фотопластинки.

Определение угла r имеет важное значение, если электроннографически устанавливается ориентационная связь двух фаз.

Индицирование электронограмм кристалла с неизвестной структурой определяется набором на них осей и наименованием их. Для этого снимают несколько электронограмм. Анализ их симметрии и измерение большого числа межплоскостных расстояний и углов между векторами обратной решетки помогают определить ячейку обратной решетки. Желательно снимать электронограммы, содержащие ряды близко расположенных рефлексов, последние будут соответствовать важным направлениям в кристалле. Такие узловые направления в обратной решетке определяют семейство кристаллографических плоскостей с большими межплоскостными расстояниями. Это даст дополнительные указания относительно размеров элементарной ячейки кристалла и, следовательно, также поможет выбрать оси обратной решетки. Величину трансляций вдоль этих осей и углы между ними можно получить из нескольких электронограмм, снятых так, что углы между последовательными положениями кристалла известны. Именно сопоставление таких взаимосвязанных сечений обратной решетки позволяют установить трехмерную систему осей обратной решетки. В частности. Одним из методов построения трехмерной обратной решетки является метод вращения. Вращая кристалл вокруг оси пучка, выставляют какое-либо важное узловое направление (иногда это может быть просто одна из осей) параллельно оси наклона кристаллодержателя, перпендикулярной пучку электронов. После этого, поворачивая кристалл на известные углы вокруг этой оси, снимают несколько электронограмм, содержащих общее узловое направление. При этом обычно одна из электронограмм соответствует координатной плоскости обратной решетки. Направление третьей оси, не лежащей в этой плоскости, можно найти, построив трехмерную модель обратной решетки.

Определив таким образом направление осей обратной решетки и осевые трансляции, легко можем вычислить набор возможных ее векторов. Затем, используя эти векторы как базисные, найдем индексы всех отражений на электронограммах.

Пространственная группа исследуемого кристалла определяется по погасаниям, закон которых легко установить после индицирования электронограмм.

Дата добавления: 2014-08-04; просмотров: 500; Нарушение авторских прав

Мы поможем в написании ваших работ!