
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПОКАЗАТЕЛИ И КРИТЕРИИ
Ответы на вопросы такого рода как, «Будет ли обостряться атмосферный фронт?», «Какая будет высота нижней границы облачности и дальность видимости?», «Возникнет ли на аэродроме гроза?», являются необходимым этапом метеорологического обеспечения, а на вопросы: «Выписывать или нет штормовое предупреждение?», «Будут ли соответствовать метеорологические условия возможностям выполнить поставленную задачу?» и другие,-являются конечной целью деятельности метеоролога. Для ответа на указанные вопросы необходимо сделать некоторые заключения о состоянии атмосферы, о возможностях прогностического метода и условиях его использования, т.е. принять решение.
Решением называется некоторое заключение, вывод об исследуемом объекте или его свойствах. Как правило, имеющаяся у синоптика информация носит статистический характер, и принимаемые на ее основе решения являются статистическими.
Статистическим решением называется некоторое заключение (вывод) об исследуемом объекте или его свойствах, полученное в результате статистической обработки информации.
В общем случае задача принятия статистических решений формулируется следующим образом. Имеется некоторый объект наблюдения, который может находиться в одном из m состояний. В процессе наблюдения за объектом получена некоторая совокупность результатов наблюдений, характеризующих состояние объекта в момент наблюдения. Необходимо на основе обработки данной совокупности результатов наблюдения принять некоторые решения о состоянии, в котором находится исследуемый объект в данный момент времени или в котором он будет находиться через некоторый промежуток времени. Легко видеть, что в первом случае речь идет о диагнозе, а во втором - о прогнозе.
Любое принятие решения сопровождается получением некоторого «выигрыша» или некоторых «потерь». Пусть, например, синоптик разработал прогноз, в котором указал наличие интенсивных осадков. Если колхозники, следуя этому прогнозу, не будут поливать поля и осадки действительно пройдут, то выигрыш будет заключаться в экономии сил и средств, используемых для полива. Если же осадков не будет, то урожай может засохнуть и колхоз получит определенные потери.
Потерями называются отрицательные последствия, сопровождающие реализацию принятого решения. Полезностью(выигрышем) называются положительные последствия, сопровождающие реализацию принятого решения. Очевидно, что для принятия решения необходимо задать некоторый алгоритм, позволяющий связать множество результатов наблюдений с множеством возможных решений.
Правило, устанавливающее закон выбора решения на множестве совокупностей сведений об изучаемом объекте, называется решающим правилом или решающей функцией.
В основе любого решающего правила лежат определенные показатели и критерии, основными из которых являются следующие.
Функция потерь L = L(m,d) показывает, каким будет экономический эффект в результате принятия некоторого решения d при осуществлении погодных условий m. Эта функция часто имеет и другие названия - функция полезности, функция выигрыша, платежная функция (матрица) и т.п. Форма представления функции потерь (выигрышей) непосредственно зависит от того, в каком виде задаются множества возможных d и m. Чаще всего встречаются случаи, когда эти множества дискретны и функция L = L(m, d) записывается в виде прямоугольной матрицы, содержащей число строк, равное числу возможных состояний погоды k, и число столбцов, равное числу S возможных хозяйственных решений. Общий вид такой матрицы представлен в табл. 1.
Во многих случаях при построении метеоролого-экономических моделей удобнее оперировать не самими значениями потерь L(m,d), а некоторыми связанными с ними разностными величинами R(m,d), показывающими, в какой степени увеличиваются потери или, соответственно, снижается прибыль, когда вместо оптимального действия выбирается другое.
Таблица 1
Общий вид матрицы потерь (выигрышей) при произвольных k и S.
| Состояния погоды М | Хозяйственные решения d | ||||||
| d1 | d2 | d3 | ... | dj | ... | dS | |
| m1 | L11 | L12 | L13 | ... | L1j | ... | L1s |
| ... | ... | ... | ... | ... | ... | ... | ... |
| mi | Li1 | Li2 | Li3 | ... | Lij | ... | Lis |
| ... | ... | ... | ... | ... | ... | ... | ... |
| mk | Lk1 | Lk2 | Lk3 | ... | Lkj | ... | Lks |
Если предположить, что исходные величины L(m,d) имеют смысл потерь, то функция R(m,d), задаваемая на всевозможных парах (m,d), будет записываться как
R(m,d) = L(m,d) - L(m,do), (1)
где L(m,do) = min L(m,d).
Аналогично, если L(m,d) - выигрыши, то
R(m,d) = L(m,do) - L(m,d), (2)
Величины R(m,d) в обоих случаях положительны и представляют собой потери, которые обусловлены несоответствием выбранных действий фактическим погодным условиям. Функцию R(m,d) принято называть риском(сожалением).
Одним из возможных путей оценки качества решающей функции dв показателях, которые можно вычислить, является определение того, насколько хороша выбранная стратегия «в среднем». Для этого используется такое понятие, как функция риска.
Функцией риска называется закон, ставящий в соответствие принятому решению d и состоянию погоды m некоторые средние потери. Определяется функция риска равенством
R(m,d) = 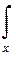 L(m,d(x)) f(x/m) dx (3)
L(m,d(x)) f(x/m) dx (3)
для непрерывных случайных величин или
R(m,d) = 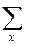 L(m,d(x)) p(x/m) (4)
L(m,d(x)) p(x/m) (4)
для дискретных случайных величин.
Задача статистического решения сводится к тому, чтобы выбрать такое решающее правило, которое обеспечило бы минимум риска или функции риска. Минимизация риска в данном случае будет целью построения решающего правила. Поэтому часто такой критерий называют целевой функцией потребителя.
В практической деятельности в качестве целевых функций кроме перечисленных выше используются и другие величины. Выбор показателей, как уже было сказано, определяется самой постановкой задачи. В частности, при оптимизации продажи товаров можно стремиться к максимальной средней прибыли, при строительстве - к минимальному времени работ, при медицинском обследовании - к наибольшему выявленному количеству (или процентной доле) больных и т.д..
В некоторых случаях для достижения цели требуется просто выполнить некоторую задачу, не учитывая какие-либо промежуточные результаты. Тогда логичным является выбор в качестве целевой функции вероятности выполнения задачи.
Как уже было сказано выше, следует различать понятия «показатель» и «критерий» выбора решения (впрочем, иногда эти понятия используются авторами как синонимы). Критерием выбора решения будем называть минимум или максимум выбранного показателя. К примеру, при обеспечении военной операции по уничтожению вражеского штаба в качестве показателя эффективности можно использовать вероятность выполнения задачи. Тогда критерием, очевидно, должна являться максимальная вероятность выполнения задачи. (Соответственно лучшим будет то решение, которое обеспечит максимум вероятности). Если целевой функцией служит время проведения посевных работ, то критерий - минимальное время и т.д.
| <== предыдущая страница | | | следующая страница ==> |
| ВВЕДЕНИЕ. Витаминные препараты -это природные вещества, которые поступаю человек с пищей, являются незаменимыми и обеспечивают нормальное течение всех видов обмена | | | ПОНЯТИЕ РЕШЕНИЯ И СТРАТЕГИИ |
Дата добавления: 2014-08-04; просмотров: 359; Нарушение авторских прав

Мы поможем в написании ваших работ!