Символьные операции с выделенными переменными

Символьные операции объединены в подменю Variable и позволяют выполнить следующие операции:

Solve – решает уравнения относительно выделенной переменной (в первой метке вводится решение выражения, во второй – переменная, относительно которой ведется решение).

,

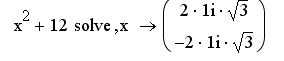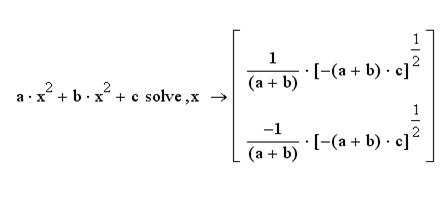
Substitute – подставляет, вместо выделенной переменной некоторое выделенное выражение или численное значение. Вместо переменной можно подставить конкретное значение.

В приведенном ниже примере в первой метке вводится выражение, в котором должна проводиться подстановка, во второй - подставляемое выражение.

.

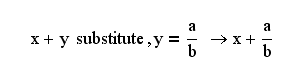Differentiate – позволяет продифференцировать выражение относительно выделенной переменной. Другие переменные этого выражения рассматриваются как константы.

Integrate – позволяет проинтегрировать выражение относительно выделенной переменной. Другие переменные этого выражения рассматриваются как константы.

Expand to Series – позволяет представить аналитическое выражения в виде ряда Тейлора.

Convert to Partial Fraction – позволяет разложить рациональную дробь на элементарные дроби относительно выделенной переменной.

В символьных операциях с выделенными переменными имеются и операции обработки матрицы.

Transpose – транспонирование матрицы.

.

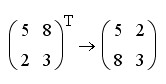Invert – определяет обратную матрицу.

.

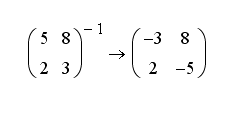Determinal – определяет определитель матрицы (определитель матрицы - это число, необходимое для решения уравнения).

.

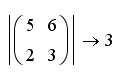7.2 Символьные операции интегральных преобразований

Этот блок содержит прямые и обратные преобразования Фурье, Лапласа и Z – преобразования.

1. Прямое преобразование Фурье по t

.

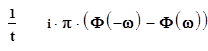2. Обратное преобразование Фурье по wt

.

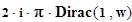3. Прямое Z – преобразование по n

.

4. Обратное Z – преобразование по n

.

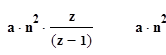Команды меню:

Evaluate – позволяют выполнить символьные преобразования

Symbolically – (в символьном виде) – выполняет символьные вычисления и обеспечивает обработку математических выражений, содержащих встроенные в систему функции. При этом выражение может быть представлено в различном виде: полиноминальном, дробно-рациональном, в виде сумм, произведений, производных, интегралов и т.д. Данная символьная операция стремится произвести все возможные числовые вычисления и представить выражения в простом виде. Возможно также выполнение этой операции над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме.

Floating Point – (переменные с плавающей запятой) – выполняет арифметические операции в выражении, результат которого должен быть представлен в форме числа с плавающей точкой. Эта команда позволяет определить точность преобразований, для этого устанавливается заданная точность. Рекомендуется брать точность не выше четырех или пяти позиций. В принципе MATHCAD позволяет представлять числа до четырех тысяч позиций. На рис.7.2. показана палитра с помощью, которой можно набрать требуемое число позиций после запятой.

Рис. 7.2. Вызов палитры переменных с плавающей запятой

Complex – символьные преобразования с комплексными переменными.

Дата добавления: 2014-08-04; просмотров: 402; Нарушение авторских прав

Мы поможем в написании ваших работ!