
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дюрация финансовых инструментов
Уровень процентного риска зависит от срока до погашения облигации – чем выше срок, тем более рискованными являются вложения в данную облигацию, при этом большее значение для инвестора имеют те года, где денежные потоки, представленные купонными выплатами, имеют больший вес в цене облигации. Следовательно, для инвестора показатель среднего срока для погашения, где года взвешены по настоящей стоимости купонных платежей, отнесенных к цене облигации, приобретает характеристику рискованности инвестиций в данную ценную бумагу.
Рассмотрим финансовый инструмент со следующим потоком платежей:
| Срок, лет | t1 | t2 | … | tk |
| Платеж, у.е. | Ct1 | Ct2 | … | Ctk |
Если требуемая доходность при начислении процентов два раза в год равна r, то дюрацией Маколея (Macaulay duration) данного финансового инструмента называется величина
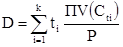 ,
,
где 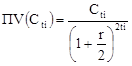 - приведенная стоимость i –го платежа, i = 1, 2, 3,…, k;
- приведенная стоимость i –го платежа, i = 1, 2, 3,…, k;
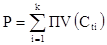 - текущая цена финансового инструмента.
- текущая цена финансового инструмента.
Модифицированная дюрация (modified duration) финансового инструмента определяется равенством
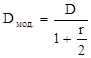 .
.
Имеет место следующее равенство:
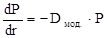 ,
,
т.е. производная цены финансового инструмента по требуемой доходности равна произведению модифицированной дюрации этого инструмента на его цену с обратным знаком.
Основное свойство дюрации – при малых изменениях требуемой доходности имеет место равенство:
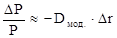 ,
,
где  - относительное изменение цены финансового инструмента при требуемой доходности на величину ∆r (положительную или отрицательную).
- относительное изменение цены финансового инструмента при требуемой доходности на величину ∆r (положительную или отрицательную).
Следовательно, 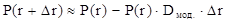 .
.
Для расчета модифицированной дюрации любого финансового инструмента с заданным потоком платежей можно использовать следующую приближенную формулу:
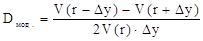 ,
,
где r – требуемая доходность при начислении процентов дважды в год;
∆y – выбранное изменение требуемой доходности;
V(r), V(r-∆y), V(r+∆y) – цены финансового инструмента при требуемой доходности равной r, r-∆y, r+∆y соответственно.
Модифицированная дюрация для портфеля облигаций – взвешенная по стоимости сумма модифицированных дюраций облигаций, входящих в этот портфель, т.е.:
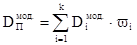 ,
,
где 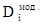 - модифицированная дюрация i-ой облигации, i = 1, 2, 3,…, k;
- модифицированная дюрация i-ой облигации, i = 1, 2, 3,…, k;
k – число облигаций в портфеле;
ωi – отношение рыночной стоимости i-той облигации к рыночной стоимости
портфеля (доля рыночной стоимости i-той облигации в рыночной
стоимости портфеля).
Основное свойство модифицированной дюрации портфеля облигаций: если требуемые доходности всех облигаций изменятся на одну и ту же достаточно малую величину, то
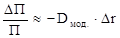 ,
,
где 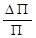 - относительное изменение цены портфеля при изменении требуемой доходности на величину ∆r.
- относительное изменение цены портфеля при изменении требуемой доходности на величину ∆r.
Если временной горизонт инвестора совпадает с дюрацией Маколея, то фактическая накопленная стоимость портфеля никогда не будет меньше его целевой накопленной стоимости. Для защиты портфеля облигаций от процентного риска применяется стратегия иммунизации портфеля облигаций, при которой в начальный момент времени формируется портфель облигация так, чтобы дюрация Маколея совпадала с временным горизонтом инвестора. Со временем портфель периодически пересматривается, чтобы каждый раз дюрация Маколея совпадала с временным горизонтом инвестора.
| <== предыдущая страница | | | следующая страница ==> |
| Относительное изменение цены купонной облигации | | | Выпуклость финансовых инструментов |
Дата добавления: 2014-02-26; просмотров: 516; Нарушение авторских прав

Мы поможем в написании ваших работ!