Моделирование в теории телетрафика

При моделировании реальный объект (или процесс) обычно представляется в идеализированной форме, упрощающей исследование. Выбор модели – сложная задача. Ее решение осуществляется с учетом множества факторов.

Во-первых, следует четко выделить цель моделирования. Одна и та же система телетрафика может изучаться с помощью разных моделей, если исследуются, например, свойства выходящего потока и влияние дисциплины обслуживания на вероятность потери заявок. Во-вторых, должны быть установлены основные причинно-следственные связи, важные для решаемой задачи. В-третьих, следует оценить желаемую точность результатов моделирования.

Существует несколько видов моделирования. Сначала в теории телетрафика были использованы методы моделирования, основанные на реальных аппаратных средствах. В частности, искусственное замыкание и размыкание шлейфа абонентской линии может считаться простейшим примером такого моделирования. Подобные эксперименты часто связывают с физическими моделями. Этим моделям свойственно изменение масштаба. К достоинствам физических моделей следует отнести их адекватность реальным объектам (или процессам). Обычно реализация этих моделей (если речь не идет об эксперименте на уже готовом оборудовании) обходится довольно дорого. Существенно то, что данный вид моделей не годится в тех случаях, когда оборудование только разрабатывается.

В настоящее время в теории телетрафика широко используется математическое моделирование. Оно незаменимо в тех случаях, когда исследование системы с помощью аналитических методов не представляется возможным. Также полезным математическое моделирование становится для проверки ряда допущений, свойственных аналитическим методам исследования систем телетрафика. Еще одна сфера применения – выбор числа членов в рядах, включающих бесконечное количество слагаемых.

Математическое моделирование систем телетрафика выполняется на ЭВМ за счет составления программы или набора программ. Эти программы имитируют процессы по обслуживанию заявок. Поэтому в теории телетрафика очень часто используется термин "имитационное моделирование".

Иногда используется сочетание физических и математических моделей. В частности, японские специалисты при изучении вероятностно-временных характеристик системы общеканальной сигнализации изготовили оборудование, а на его входе имитировали с помощью программного датчика случайных чисел входящий поток заявок – сигнальных единиц.

Моделирование случайных чисел – важный этап создания имитационных моделей. Известны два способа получения случайных чисел:

· использование физических генераторов (датчиков) случайных чисел (шум в радиоэлектронных приборах и трактах, радиоактивное излучение);

· составление программ, позволяющих получить псевдослучайные числа (они могут быть очень близки к случайным числам).

В настоящее время используются исключительно программные датчики. Обычно случайные числа генерируются так, чтобы они принадлежали интервалу 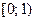. При этом закон распределения должен быть равномерным. Известно, что для интервала 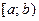функци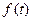и и 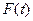определяются следующим образом:

, .

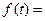
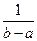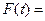
На рисунке показаны функци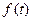и и 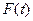. Основные характеристики равномерного распределения представлены в таблице.

Равномерное распределение на интервале

Математическое ожидание	Дисперсия	Асимметрия	Эксцесс
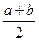
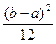
			–1,2

Очевидно, что для интервала 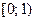среднее значение равно 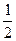, а дисперсия – .

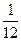Моделированием случайной величины называют процесс получения ее значений. Это означает, что для формирования потока вызовов, поступающих, например, в АТС, следует разработать процесс, который позволяет выделять моменты занятия входов на ступени абонентского искания. Ступень абонентского искания в АТС – с точки зрения имитационной модели – может рассматриваться как система телетрафика.

Случайные числа, получаемые с помощью программных генераторов, необходимо проверить с точки зрения закона их распределения на интервале 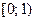. Для этого можно использовать сравнение статистического и эмпирического распределений, выбрав заранее критерий согласия. Часто используется критерий Пирсона – .

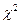Для того чтобы убедиться в "похожести" полученного распределения и закона равномерной плотности, целесообразно проверить математическое ожидание случайной величины (оно должно быть близким к 0,5), коэффициент вариации (он должен быть равен примерно 0,577), коэффициент асимметрии (он должен быть близок к нулю) и коэффициент эксцесса (он не должен заметно отличаться от минус 1,2).

Получив случайные (псевдослучайные) числа, необходимо перейти к формированию последовательности случайных величин с исследуемым законом распределения. Обычно используется один из следующих приемов:

· метод обратных функций (то есть, прямого преобразования равномерно распределенных случайных чисел);

· приближенные методы;

· метод отсеивания чисел из первоначальной последовательности случайных чисел (метод генерации Неймана);

· методы, основанные на центральной предельной теореме.

Допустим, что случайная величина 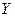непрерывна, а соответствующая плотность распределения вероятности задана функцией 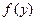. Тогда функция распределения задана известным выражением:

.

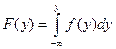Обычно в качестве нижнего предела интегрирования в теории телетрафика используется ноль.

Теорема. Если случайная величина 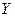имеет плотность распределения вероятности 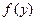, то распределение случайной величины

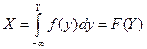
является равномерным на интервале 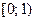. Из этой теоремы следует Правило: для того чтобы найти возможное значение 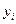непрерывной случайной величины 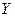, надо выбрать случайное число 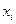и решить относительно 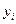такое уравнение:

.

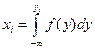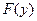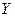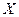Справедливо и обратное утверждение. Если – функция распределения непрерывной случайной величины , а – случайная величина с равномерным законом распределения на интервале 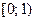, то случайная величина 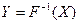имеет функцию распределения 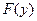. В данном случае 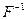– функция, обратная по отношению к .

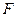Таким образом, необходимо:

· реализовать случайную величину 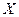, которая распределена равномерно на интервале ;

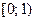· вычислить значение случайной величины 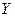по формуле .

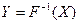Один из важных для теории телетрафика случаев – простейший входящий поток. Это означает, что случайная величина 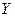подчиняется экспоненциальному закону:

.

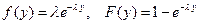Необходимо найти формулу для моделирования случайной величины 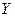с помощью равномерно распределенной случайной величины .

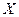Шаг 1. Находится функция, обратная по отношению к 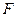. Известно, что 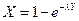. Решение относительно 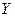тривиально: .

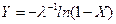Шаг 2. Очевидно, что случайная величина 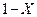(так же как и случайная величина 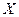) равномерно распределена на отрезке 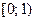. Поэтому справедлива также и формула следующего вида: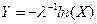

Шаг 3. Теперь числа с экспоненциальным распределением могут быть получены из значений 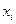по такой формуле: .

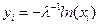К сожалению, не всегда удается решить соответствующие уравнения в явном виде. Приходится прибегать к приближенным методам. В частности, используется кусочная аппроксимация функций .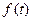

Три других метода получения требуемых законов распределения описаны в работах по моделированию. Одна из последних публикаций – монография [1].

Входящий поток заявок на входе СМО (системы телетрафика) может быть задан последовательностью появления требований: 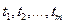. С практической точки зрения удобнее оперировать длительностью промежутка между соседними требованиями: 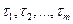. Способ формирования величин 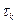с заданным законом распределения был изложен выше. Теперь необходимо определить свойства СМО и проследить за временами обслуживания заявок и соответствующими процессами (потери и задержки).

В качестве примера моделирования рассматривается алгоритм, предложенный в монографии [2].

Дата добавления: 2014-08-09; просмотров: 574; Нарушение авторских прав

Мы поможем в написании ваших работ!