
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расчёт надёжности системы с постоянным поэлементным резервированием
При поэлементном резервировании резервируются отдельные элементы системы.
Определим количественные характеристики надёжности системы.
Введём обозначения:
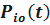 ,
, 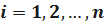 – вероятность безотказной работы элемента ij на интервале времени (0, t).
– вероятность безотказной работы элемента ij на интервале времени (0, t).
Запишем вероятность отказа i-ой группы.
Имеем 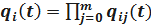 ,
, 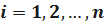 .
.
Запишем вероятность безотказной работы i-й группы. Имеем
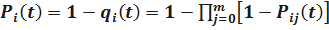 .
.
Запишем вероятность безотказной работы системы с поэлементным резервированием
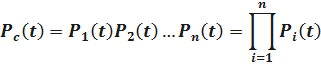
или
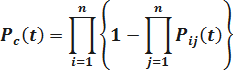
Для равнонадёжных элементов системы имеем: 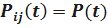
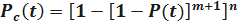 ;
;
1.20 Режим облегченного (тёплого) резерва
Рассмотрим случай, когда время безотказной работы всех элементов изделия подчиняется экспоненциальному закону распределения. В этом случае процессы, характеризующие работу изделия являютсямарковскими. Для определения характеристик надёжности можно использовать математический аппарат теории марковских случайных процессов.
В режиме облегченного резерва резервные элементы находятся в режиме недогрузки до момента их включения в работу. Пусть 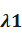 - интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу.
- интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу. 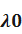 - интенсивность отказа резервного элемента в состоянии работы.
- интенсивность отказа резервного элемента в состоянии работы.
Введём в рассмотрение состояния 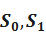 ,
, 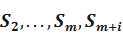 .
.
S0 - основной элемент исправен и работает, ш резервных элементов исправны и находятся в режиме недогрузки.
S1 - основной элемент отказал, работает 1 - ый резервный элемент, (m – 1) резервные элементы исправны и находятся в режиме недогрузки.
S2 - отказал 1 - ый резервный элемент, работает 2-ой резервный элемент, (m - 2) резервных элементов исправны и находятся в режиме недогрузки.
Si- отказал i- й резервный элемент, работает i- й резервный элемент, (m- i) резервных элементов исправны и находятся в режиме недогрузки.
Sm- отказал (m- 1) - ый элемент, работает m- ый резервный элемент.
Sm+1- отказал m-ый резервный элемент.
Запишем систему дифференциальных уравнений Колмогорова. Для этого введём обозначения:
P0(t) - вероятность нахождения резервированной системы в момент времени tв состоянии S0.
Pi(t) - вероятность нахождения резервированной системы в момент времени tв состоянии Si, i= 0, 1,… m, m+ 1.
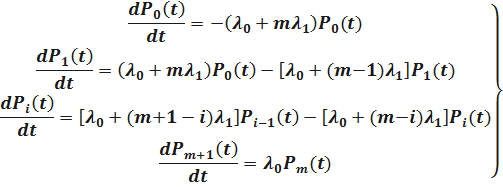
Начальные условия:
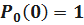
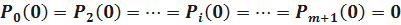 .
.
Применим к системе дифференциальных уравнений Колмогорова преобразования Лапласа. Получим систему линейных алгебраических уравнений вида: Pi(t) – оригинал
Pi(S) – изображение по Лапласу
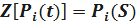 .
.
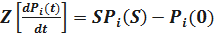 ,
, 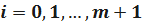

Решая систему уравнений получим
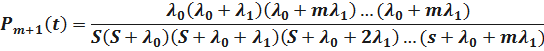
Найдём оригинал 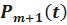 . Имеем
. Имеем
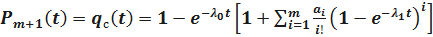 ;
;
где 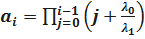 .
.
Здесь 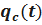 – вероятность отказа резервированной системы с облегчённым резервированием.
– вероятность отказа резервированной системы с облегчённым резервированием.
Определим вероятность безотказной работы системы с облегченным резервированием. Имеем:
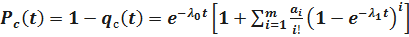 ;
;
Определим среднее время безотказной работы системы с облегченным резервированием. Имеем:
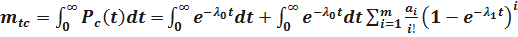 .
.
Формула бинома Ньютона
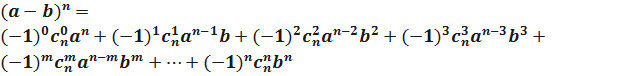 .
.
где 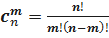
При 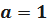 имеем:
имеем:
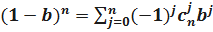 ;
;
 ;
;
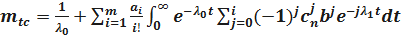 .
.
Выполнив преобразования, получим:
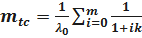 ; где
; где 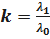 .
.
Определим частоту отказов 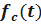 резервированной системы. Имеем
резервированной системы. Имеем
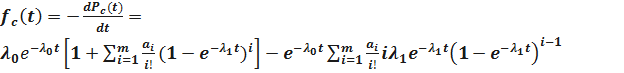 ;
;
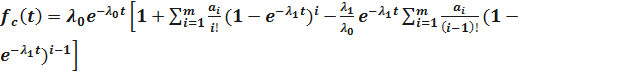 ;
;
Определим интенсивность отказов  резервированной системы. Имеем
резервированной системы. Имеем
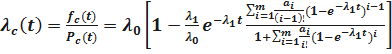 ;
;
| <== предыдущая страница | | | следующая страница ==> |
| Расчёт надёжности системы с постоянным общим резервированием | | | Режим нагруженного резерва |
Дата добавления: 2014-08-09; просмотров: 408; Нарушение авторских прав

Мы поможем в написании ваших работ!