ОШИБКИ ИЗМЕРЕНИЙ И МЕРЫ ТОЧНОСТИ

1.1. Общие сведения об измерениях

Под измерением следует понимать определение численного значения физической величины с помощью специальных технических средств, или это есть процесс сравнения какой-либо величины с другой ей однородной величиной, принятой за единицу. Измеряемая величина и единица измерения не соизмеримы друг с другом, что приводит к возникновению ошибок.

В процессе измерения участвуют следующие элементы: объект измерения; наблюдатель; инструмент; внешняя cреда. Все это образует условия измерения, которые и являются источниками возникновения ошибок.

Любое измерение, как бы оно тщательно не выполнялось, сопровождается ошибкой, численно равной разности между результатом измерения и истинным значением измеряемой величины. Это значение можно назвать истинной ошибкой измерения

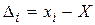, (1.1)

гдe x_i - результаты измерения;

X- истинное значение измеряемой величины.

Значения большинства величин получают как в результате непосредственных измерений, так и с помощью вычислений, т.е. прямым и косвенным способами.

Объектами измерений могут быть как однородные, так и неоднородные величины. Например, в триангуляции измеряются однородные величины (углы), а в полигонометрии - неоднородные (углы и длины линий). Вместе с тем основные определяемые величины - координаты пунктов - в том и другом случае являются однородными.

Различают необходимые и избыточные измеренные величины. Необходимыми являются измеренные величины, достаточные для однозначного определения значений искомых величин. Измерения, выполненные сверх необходимых, будут избыточными. Они играют в теории ошибок важную роль, так как позволяют:

контролировать качество выполненных работ, выявляя результаты с грубыми ошибками;

оценить точность выполненных измерений;

определять наиболее надежные значения измеряемых величин.

По отношению к точности результаты измерений можно подразделить на равноточные и неравноточные. Равноточными являются такие измерения, которые выполняются

а) одним и тем же инструментом или разными инструментами, но с одинаковой точностью;

б) одними и теми же методами или способами;

в) в одних и тех же условиях.

Если какое-либо из перечисленных пунктов не соблюдается, то измерения относятся к неравноточным.

Особым качеством результатов измерений является их взаимная независимость. Наиболее полная независимость достигается в том случае, если измерения произведены в различных условиях. В своей же массе большинство результатов измерений можно отнести к зависимым. Однако практика геодезических работ позволяет пренебречь в пределах точности измерений возникающими в этом случае зависимостями.

1.2. Виды ошибок измерений

Причинами возникновения ошибок в результате измерений являются:

1) изменение величины или состояния объекта в процессе измерения;
2) личные ошибки наблюдателя;

3) инструментальные ошибки измерений;

4) влияние внешней cреды.

Возникшие при этом ошибки можно подразделить на три вида: грубые, систематические и случайные.

К грубым ошибкам относятся промахи, просчеты при измерениях, а также ошибки, превосходящие допустимые значения. Грубые ошибки выявляются повторными измерениями и исключаются из результатов. Следовательно, задача сводится к организации контроля наблюдений.
Если среднее арифметическое из ошибок равноточных измерений стремится к некоторому пределу, отличному от нуля, при увеличении числа измерений до бесконечности, то такие ошибки называются систематическими. К систематическим ошибкам относятся составляющие общей ошибки измерений, которые постоянны или закономерно изменяются при повторных измерениях одной и той же величины. Систематические ошибки по характеру действия классифицируют: на сохраняющие знак и величину; меняющиеся по величине, но сохраняющие знак (одностороннее действующие); изменяющиеся по какому-либо функциональному закону. Анализ причин возникновения систематических ошибок позволяет частично или полностью исключить их из результатов измерений. Величина систематических ошибок зависит от методики измерений.

Если среднее арифметическое из ошибок равноточных измерений одной и той же величины стремится к нулю при увеличении числа измерений до бесконечности, то такие ошибки называются случайными. Случайная ошибка является той частью общей ошибки, которая меняется при повторных измерениях одной и той же величины. Случайные ошибки по величине чаще всего больше систематических, но из-за взаимных компенсаций их влияние на окончательный результат может быть слабее.

1.3. Свойства случайных ошибок

Случайные ошибки измерений подчиняются нормальному закону распределения с плотностью

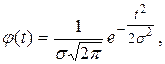
(1.2)
где t - текущее значение случайной ошибки измерений;
s - среднее квадратическое отклонение (стандарт) генеральной совокупности этих ошибок.

Из анализа функции (1.2) имеем:

1) функция достигает максимальных значений при t = 0;

2) функция четная, т.е. f(t) = f(-t); отсюда следует, что кривая симметрична относительно значения t = 0;

3) математическое ожидание случайных ошибок измерений определится согласно

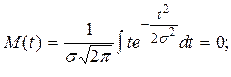(1.3)

4) дисперсия случайных ошибок измерений запишется в виде

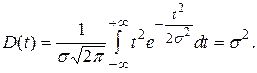
(1.4)

Отсюда среднее квадратическое отклонение

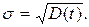(1.5)

Равенство (1.2) носит название уравнения кривой Гаусса. Свойства ее совпадают с кривой нормального распределения (рис.1). Отсюда получим следующие свойства случайных ошибок измерений.

1. При данных условиях измерений случайные ошибки не могут превзойти по абсолютной величине определенного предела, т.е.

j ( t ) ½D½ = D_пр= 3s . (1.6)

2. Малые по абсолютной величине

ошибки встречаются чаще, чем

большие.
3. Положительные ошибки появляются

так же часто, как и равные им по

абсолютной величине отрицательные

ошибки, т.е.

-3s -2s -s 0 s 2s 3s t p (D < 0) = p ( D > 0) = 0,5. (1.7)

Рис. 1

4. Среднее арифметическое из случайных ошибок измерений одной и той же величины стремится к нулю при неограниченном возрастании числа измерений, т.е.

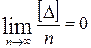. (1.8)

Если 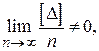то в этом случае систематическое влияние полностью не исключено.

1.4. Принцип арифметической средины

Пусть даны результаты равноточных измерений одной величины x₁, x₂, ... , x_n . При этом следует иметь в виду, что истинное значение X измеряемой величины известно.

Составим ряд истинных ошибок результатов измерений согласно равенству (1.1)

D₁ = x₁ - X ;
D₂= x₂ - X ; (1.9)
.......................
D_n= x_n - X .

Равенства (1.9) почленно сложим, в результате получим следующее значение:

.

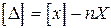Полученное равенство разделим на n , вследствие чего будем иметь

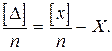(1.10)

Введем обозначение 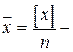среднее арифметическое значение измеряемой величины. Тогда

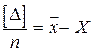. (1.11)

На основании четвертого свойства случайных ошибок можно утверждать, что 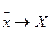при n ® ¥, т.е. среднее арифметическое из результатов равноточных измерений стремится к истинному значению этой величины при неограниченном возрастании числа измерений.
Среднее арифметическое из данного ряда равноточных измерений принимается за наиболее надежное значение и при конечном числе измерений.

1.5. Меры точности результатов измерений

Для оценки точности отдельного измерения некоторой величины необходимо определить возможные отклонения результатов измерения этой величины от ее истинного значения. Суждение о точности выполненных измерений можно получить по степени различия результатов измерений в ряду: чем больше разбросаны результаты в ряду, тем сильнее рассеивание (дисперсия) ряда, тем менее точны измерения.

Возьмем два ряда измерений, выполненных в различных условиях, истинные ошибки которых будут:

-3, +2, +4, -2, -1, 0, +4, -3, +2, -3;
0, -1, +7, +2, -1, -1, -8, 0, +3, -1.

Сопоставляя ряды, видим, что разброс ошибок во втором ряду больше, чем в первом. Следовательно, условия измерений в первом случае более благоприятны.

Найдем среднюю ошибку, которая определяется по абсолютным значениям ошибок ряда

(1.12)

В результате вычислений получим следующие значения средних ошибок J₁ = 2,4; J₂ = 2,4. Как видим, оба значения одинаковы. Это объясняется тем, что J недостаточно чувствительно к наличию крупных ошибок.
В качестве меры точности Гаусс предложил принять среднее квадратическое отклонение или среднюю квадратическую ошибку согласно равенству (1.5)

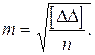(1.13)

Вся теория математической обработки результатов измерений построена на использовании средней квадратической ошибки, которая обладает рядом преимуществ:

1) при вычислении нет необходимости учитывать знак величины D_i отдельных ошибок;

2) большие по абсолютному значению величины D_i после возведения в степень увеличивают ее численные значения, создавая своего рода “запас прочности”;

3) по формуле (1.13) значение средней квадратической ошибки m получается со знаком “ ± “, что соответствует природе случайных ошибок.
Отличием средней квадратической ошибки m от стандарта s является то, что средняя квадратическая ошибка - величина эмпирическая, вычисляемая из ограниченного числа измерений, а стандарт - величина постоянная, характеризующая бесконечную совокупность данного вида измерений. Это - величина теоретическая. При n ® ¥ , m ® s. Для нашего примера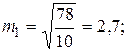

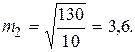
Из сравнения m₁ и m₂ cледует, что условия измерений для первого ряда лучше, чем для второго ряда.

Так как s всегда остается неизвестным, то приходится пользоваться его “оценкой” m, т.е. m » s, которое в свою очередь определяется с ошибкой m_m

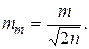(1.14)

Cуществует связь между средней и средней квадратической ошибками при n ® ¥

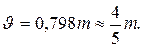(1.15)

Иногда в качестве меры точности используют вероятную ошибку r, которая делит ряд ошибок, расположенных в порядке возрастания их абсолютных значений, пополам. При n ® ¥ вероятная ошибка r связана со средней квадратической ошибкой зависимостью

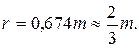(1.16)

1.6. Вероятностное обоснование применения теории ошибок измерений

Знание функции плотности распределения случайных ошибок измерений дает возможность для решения целого ряда задач, возникающих при различных геодезических работах: определение наиболее вероятного значения при многократных измерениях; установление предельных значений (допусков) для конкретного вида работ; вычисление вероятности появления случайной ошибки в определенном интервале; выявление предельных значений, за которыми ошибки можно квалифицировать как грубые. Для этого воспользуемся функцией Лапласа, имеющей следующий вид

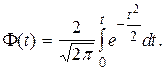(1.17)

Вероятность того, что любая случайная величина X примет значение, принадлежащее интервалу (a, b), можно выразить через функцию распределения

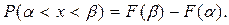(1.18)

Перейдем к нормированной случайной величине t . Неравенства a < x < b и 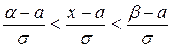равносильны. Поэтому вероятности этих неравенств равны между собой

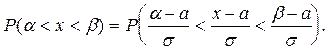(1.19)

Используя равенство (1.18), запишем

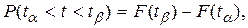(1.20)

где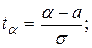

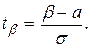
Считая, что нормированная случайная величина t имеет нормальное распределение, и используя определение интегральной функции , получим

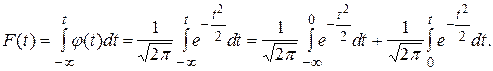(1.21)
Первое слагаемое числено равно половине площади под нормированной кривой распределения; второе слагаемое является выражением функции Лапласа. Итак, для нормально распределенной случайной величины имеем

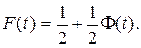(1.22)

Используя формулу (1.22) в выражении (1.20), получим

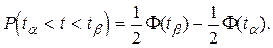(1.23)

1.7. Определение вероятности отклонения случайной величины от ее математического ожидания

Определим вероятность того, что нормально распределенная величина X отклоняется от своего математического ожидания на величину меньшую чем e, т.е. найдем вероятность осуществления неравенства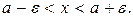

Перейдя к нормированной случайной величине t , имеем

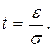(1.24)

Согласно равенству (1.23)

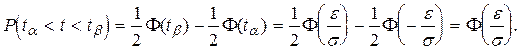(1.25)

Окончательно получим

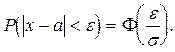(1.26)

При 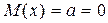равенство (1.26) примет вид

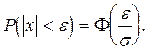(1.27)

Выразив отклонение случайной величины X в долях среднего квадратического отклонения, т.е. положив 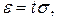равенство (1.26) можно записать

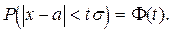(1.28)

Таким образом, значение 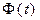при заданном t определяет вероятность того, что отклонение нормально распределенной величины по абсолютному значению меньше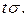

При t = 1 имеем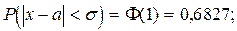

при t = 2 имеем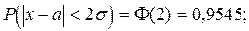

при t = 3 имеем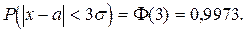

Из последнего равенства следует, что практически рассеивание случайной величины укладывается на участке 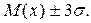Вероятность того, что случайная величина X попадает за этот интервал очень мала, а именно равна 0,0027, т.е. это событие можно считать практически невозможным. На приведенном рассуждении основано “правило трех сигм”, которое формулируется следующим образом: если случайная величина имеет нормальное распределение, то отклонение этой величины от ее математического ожидания по абсолютной величине не превосходит утроенного среднего квадратического отклонения.

1.8. Предельная ошибка результата измерения

По величине средней квадратической ошибки, определяющей условия измерения, можно установить предельную ошибку

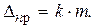
(1.29)

Ошибки, большие предельной, считаются грубыми. Из предыдущего параграфа было установлено: P(ïDï< s) = 0,6827; P(ïDï< 2s) = 0,9545; P(ïDï< 2,5s) = 0,9876; P(ïDï< 3s) = 0,9973, т.е. случайная ошибка измерения может превосходить среднюю квадратическую ошибку (m) в 32 случаях из 100, удвоенную (2m) - в 5 случаях из 100, утроенную (3m) - в 3 случаях из 1000. Следовательно, согласно “правила трех сигм” для различных геодезических работ величину k принимают равную 3, т.е.

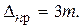(1.30)

При вычислении допустимых невязок k = 2 и тогда

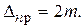(1.31)

1.9. Абсолютные и относительные ошибки

Такие ошибки, как средняя (J), средняя квадратическая (m), вероятная (r), истинная (D) и предельная (D_пр), являются абсолютными ошибками. Они всегда выражены в единицах измеряемой величины, т.е. имеют одинаковую с измеряемой величиной размерность.
Часто возникают случаи, когда разные по величине объекты измеряют с одинаковыми абсолютными ошибками. Например, средняя квадратическая ошибка измерения линий длиной: l₁ = 100 м и l₂ = 1000 м, составила m = 5 см. Возникает вопрос: какая же линия измерялась точнее ? Чтобы избежать неопределенности, точность измерений ряда величин оценивают в виде отношения абсолютной ошибки к значению измеряемой величины. Полученное отношение называется относительной ошибкой, которую обычно выражают дробью с числителем, равным единице.
Наименование абсолютной ошибки определяет и название соответствующей ей относительной ошибки измерения [ 1 ].

Пусть x - результат измерения некоторой величины. Тогда
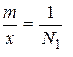- cредняя квадратическая относительная ошибка;

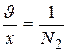- средняя относительная ошибка;

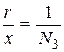- вероятная относительная ошибка;

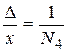- истинная относительная ошибка;

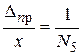- предельная относительная ошибка.

Знаменатель N относительной ошибки необходимо округлять до двух значащих цифр с нулями:

m_x = 0,3 м; x = 152,0 м;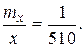

m_x = 0,25 м; x = 643,00 м; .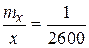

m_x = 0,033 м; x = 795,000 м;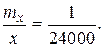

Как видно из примера, чем больше знаменатель дроби, тем точнее выполнены измерения.

1.10. Ошибки округления

При обработке результатов измерений немаловажную роль играют ошибки округления, которые по своим свойствам можно отнести к случайным величинам [ 2 ]:

1) предельная ошибка одного округления составляет 0,5 единицы удерживаемого знака;

2) большие и меньшие по абсолютной величине ошибки округления равновозможны;
3) положительные и отрицательные ошибки округления равновозможны;
4) математическое ожидание ошибок округления равно нулю.
Эти свойства позволяют отнести ошибки округления к случайным величинам, имеющим равномерное распределение. Непрерывная случайная величина X имеет равномерное распределение на интервале [a, b], если на этом интервале плотность распределения случайной величины постоянна, а вне его равна нулю (рис. 2), т.е.

j 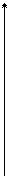(x ) 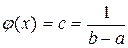. (1.32)

Функция распределения F(x)

с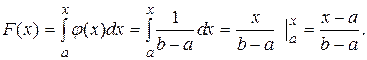

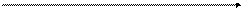a b x (1.33)

Рис. 2 Математическое ожидание

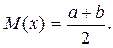(1.34)

Дисперсия
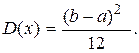(1.35)

Среднее квадратическое отклонение

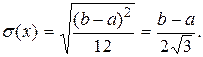(1.36)

Для ошибок округления

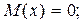
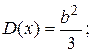
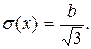(1.37)

Следовательно, средняя квадратическая ошибка округления m_о вычислится согласно

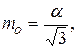
(1.38)

где a = 0,5.

Подставляя это значение в равенство (1.38), получим

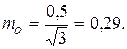
Как видно из примера, m_c незначительно отличается от ошибки измерения m.

В вычислительной практике для уменьшения влияния ошибок округления промежуточные результаты принимают на порядок выше результатов измерения. Например, если результаты линейных измерений имеют ошибку 1 мм, то промежуточные значения определяют с точностью до 0,1 мм.

1.11. Ошибки функций измеренных величин

В общем случае найдем среднюю квадратическую ошибку M_F некоторой функции вида

F = f (x₁ , x₂, . . . , x_n ), (1.39)

где x_i - коррелированные аргументы, связанные между собой зависимостями и полученные из наблюдений.

При этом будем иметь в виду, что средние квадратические ошибки результатов измерений m₁, m₂, . . . , m_n известны. Кроме этого, предположим, что X₁, X₂, . . . , X_n - истинные значения аргументов. Каждая величина измерялась k раз, т. е.

для X₁ : x₁₁, x₁₂, . . . , x_1k ;

для X₂ : x₂₁, x₂₂, . . . , x_2k;

. . . . . . . . . . . . . . . .

для X_n : x_n1, x_n2, . . . , x_nk.

Для каждой серии наблюдений получим значения оцениваемой функции (1.39):

F₁= f ( x₁₁, x₁₂, . . . , x_1n ) ;

F₂ = f ( x₂₁, x₂₂, . . . , x_2n ) ;

. . . . . . . . . . . . . . . . . . . . . . (1.40)

F_k = f ( x_k1, x_k2, . . . , x_kn ) .

Используя равенство (1.1), получим вместо уравнений (1.40) следующие зависимости:

F₁ = f ( X₁ + D ₁₁, X₂ + D₂₁, . . . , X_n + D_n1 ) ;

F₂ = f ( X₁ + D₁₂, X₂ + D₂₂, . . . , X_n + D_n2 ) ; (1.41)

. . . . . . . . . . . . . . . . . . . . . . . . .

F_k = f ( X₁ + D_1k, X₂ + D_2k, . . . , X_n + D_nk ) .

Разложив равенства (1.41) в ряд Тейлора и ограничиваясь в виду малости ошибок измерений первыми степенями разложения, получим

F₁ = f ( X₁, X_2,..., X_n ) +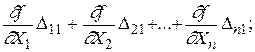

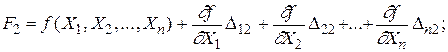(1.42)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

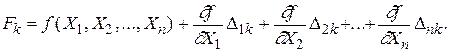Учитывая, что истинная ошибка функции

,

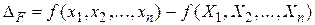получим систему случайных ошибок функций независимых величин

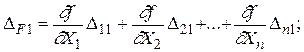
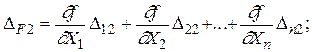(1.43)

. . . . . . . . . . . . . . . . . . . . . . .

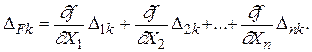
Возведя каждое равенство системы (1.43) в квадрат, просуммировав полученные значения и разделив их на k, придем к следующему уравнению:

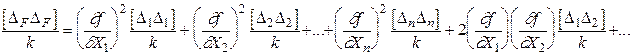
(1.44)

В математической статистике доказывается следующая теорема [ 2 ]: “Среднее значение произведения случайных величин равно произведению средних значений сомножителей”

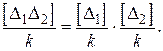(1.45)

Согласно четвертому свойству случайных ошибок каждое из сомножителей равенства (1.45) стремится к нулю при неограниченном возрастании числа измерений. Поэтому можно утверждать, что и

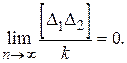(1.46)

Перейдем к средним квадратическим ошибка функции независимых величин, учитывая равенство (1.13), а также условие (1.46)
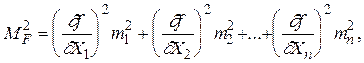(1.47)

где m_l - cредние квадратические ошибки измеренных величин.

Если аргументы зависимы (коррелированы), то для средних значений произведений ошибок этих величин при k ® ¥ справедливо равенство [ 1 ]

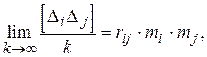(1.48)

где r_ij - коэффициент корреляции между зависимыми аргументами.
C учетом равенства (1.48) выражение (1.44) примет следующий вид 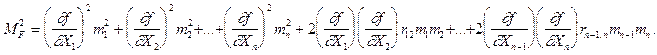(1.49)

1.12. Типовые примеры. Функция произведения непосредственно измеренного аргумента на постоянный коэффициент

Функция имеет следующий вид

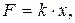(1.50)

где x - величина, измеренная с ошибкой m ;

k - постоянный коэффициент.

Частная производная от функции (1.50) по измеренной величине

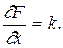
Используя равенство (1.47), получим

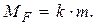(1.51)

Cредняя квадратическая ошибка произведения непосредственно измеренной величины на постоянный коэффициент равна произведению этой постоянной на среднюю квадратическую ошибку измеренного аргумента.

1.12.2. Функция линейного вида

Исходная функция представлена следующей зависимостью:

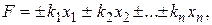(1.52)

где k_i - некоторые постоянные коэффициенты;

x_i - независимые величины, измеренные со средними квадратическими ошибками m_i.

Находим частные производные функции по независимым аргументам и, подставляя в формулу (1.13), получаем

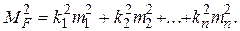(1.53)

Если k₁ = k₂ = ... = k_n = 1, то ошибка линейной функции составит

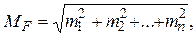(1.54)

т.е. средняя квадратическая ошибка суммы или разности независимо измеренных величин равна корню квадратному из суммы квадратов ошибок аргументов. Если при этом m₁= m₂ = ...= m_n = 1, то
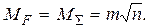(1.55)

Средняя квадратическая ошибка алгебраической суммы n равноточно измеренных величин в корень квадратный из n раз больше ошибки одного измерения.

Следовательно, накопление ошибок происходит пропорционально корню квадратному из числа измеряемых величин.

1.13. Средняя квадратическая ошибка простой арифметической средины

Дан ряд результатов равноточных измерений одной величины

x_{1 ,} x₂ , . . . , x .

Представим формулу для вычисления простой арифметической средины в виде

`x = 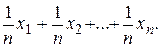(1.56)

Согласно (1.47) будем иметь

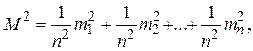(1.57)

где m₁ = m₂ = ... = m_n = m . Следовательно, равенство (1.57) примет следующий вид

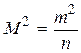
и окончательно запишем

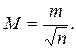(1.58)

Итак, средняя квадратическая ошибка простой арифметической средины в корень квадратный раз из числа измерений меньше средней квадратической ошибки одного измерения.

1.14. Формула Бесселя

Выполнив n повторных измерений одной и той же величины, вычислим отклонения результатов этих измерений от арифметической средины

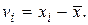
Получим формулу для оценки точности результата измерения через отклонения от арифметической средины, но предварительно рассмотрим свойства отклонений v_i [ 2 ].

Первое свойство. Алгебраическая сумма отклонений результатов равноточных измерений одной и той же величины от простой арифметической средины равна нулю при любом числе измерений.
Возьмем ряд отклонений от арифметической средины

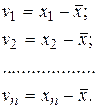( 1.59 )

Суммируя левую и правую части равенства (1.59) , получим

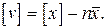
Полученное равенство разделим на n

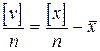. (1.60)

Поскольку правая часть равенства (1.60) равна нулю, то и [n] = 0.

Второе свойство. Сумма квадратов отклонений результатов равноточных измерений от простой арифметической средины меньше суммы квадратов отклонений этих же результатов от любой другой величины, не равной простой арифметической средины, т.е. если x¢ ¹ `x , то

[ vv ] < [ ee ] , (1.61)

где

v_i =x_i - `x , e_i = x_i - x¢ .

Докажем второе свойство отклонений v_i алгебраическим путем. Вычтем v_i из e_i по частям: из правого равенства левое

e_i - v_i = x_i - x¢ - x_i + `x = `x - x¢ = c . (1.62)

Для n числа наблюдений получим ряд отклонений e_i

e₁ = v₁ + c ,

e₂ = v₂ + c , (1.63)

. . . . . . . . .

e_n = v_n + c .

Возведем в квадрат равенства (1.63) и, суммируя левую и правую части, получим

[ ee ] = [ vv ] + nc² + 2c [ v ] . (1.64)

Но член 2c [ v ] = 0 по первому свойству отклонений v_i , тогда

[ ee ] = [ vv ] + nc² . (1.65)

Из формулы (1.65) следует, что

[ ee ] > [ vv ]

на положительное число nc² , вне зависимости от того, x¢ больше`x, или меньше. Таким образом, при x¢ ¹ x

[ vv ] < [ ee ], (1.66)

что и требовалось доказать.

Для решения поставленной в начале данного параграфа задачи определим связь между истинными ошибками D _i и отклонениями v_i . Напишем

D_i =x_i - X ; v_i = x_i - .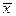

Cоставим разность

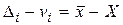. (1.67)

Возведем в квадрат равенства (1.67) и почленно просуммируем

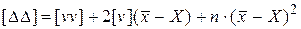. (1.68)

Согласно первому свойству отклонений имеем

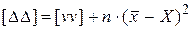. (1.69)

В равенстве (1.69) левая часть согласно формуле Гаусса равна

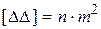. (1.70)

Разность 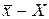данного равенства соответствует средней квадратической ошибке значения среднего арифметического из результатов измерений, т.е. равна М. Тогда с учетом вышеизложенного получим вместо равенства (1.69) следующее

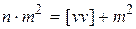
или

.

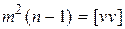Откуда средняя квадратическая ошибка результата измерения составит

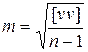. (1.71)

Средняя квадратическая ошибка вычисления ошибки согласно формуле (1.71) равна

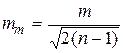. (1.72)

1.15. Влияние систематических ошибок на точность отдельных измерений

Закономерности возникновения случайных и систематических ошибок различны. Систематические ошибки подчиняются функциональным закономерностям, а случайные - статистическим. Рассмотрим влияние систематических ошибок на точность определения одного результата. Общая ошибка в этом случае составит

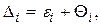(1.73)

где e_i - случайная составляющая общей ошибки измерения;

Q_i - систематическая составляющая.

В геодезической практике принято, если один из источников общей ошибки характеризуется средней квадратической ошибкой, не превышающей 1/3 средней квадратической ошибки, характеризующей другой источник, то первым можно пренебречь [ 3 ]

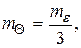(1.74)

тогда

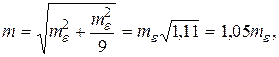
т.е. значение средней квадратической ошибки m, если пренебречь систематической ошибкой, уменьшится всего на 5%.

1.16. Оценка точности функции при наличии систематических ошибок

Определим совместное влияние случайных и систематических ошибок на отдельные результаты измерений. Будем считать, что общая ошибка содержит постоянную систематическую часть Q. Тогда ряд ошибок измерений предстанет в виде

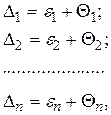(1.75)

где D_i - общая ошибка измерений;

e_i - случайная составляющая;

Q_i - систематическая составляющая.

Равенства (1.75) почленно возведем в квадрат

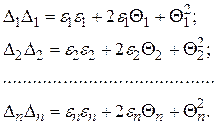(1.76)
Учитывая, что Q₁ = Q₂ = ¼ = Q_n = Q , просуммируем полученные значения, а сумму разделим на n т.е.

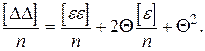(1.77)

Второй член правой части равенства (1.77) cогласно четвертому свойству случайных ошибок равен нулю. Переходя к средним квадратическим ошибкам, получим

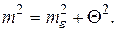(1.78)

Аналогично определяется средняя квадратическая ошибка функции

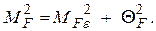(1.79)

Первое слагаемое определяется согласно (1.47)

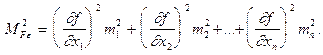(1.80)

Величина систематической ошибки определится из следующего выражения [ 2 ]

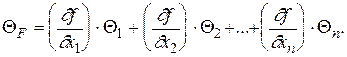(1.81)

Тогда
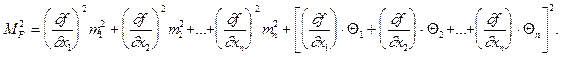(1.82)

1.17. Оценка точности равноточно измеренных величин при систематическом влиянии

Пусть слагаемые x₁, x₂, ... , x_n результаты равноточных измерений со средней квадратической ошибкой m_e и постоянной систематической ошибкой Q. Тогда при

y = x₁ + x₂ + ... + x_n

имеем
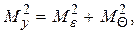(1.83)

где 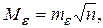а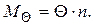

Тогда средняя квадратическая ошибка суммы составит

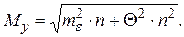(1.84)

1.18. Принцип равных влияний

При проектировании геодезических работ рассчитывают точность предстоящих измерений, пользуясь формулами теории ошибок измерений. При этих расчетах встречается задача, в которой по известному виду функции F требуется рассчитать точность измерений аргументов. Чтобы иметь определенное решение, применяют принцип равных влияний.

Пусть дана функция общего вида

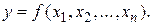(1.86)

На основании равенства (1.47) средняя квадратическая ошибка функции общего вида определится

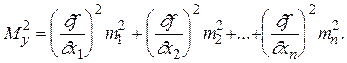
Предположим, что

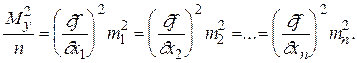
Откуда

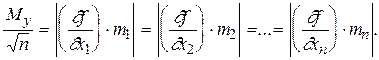(1.87)

Эти соотношения позволяют вычислить средние квадратические ошибки аргументов при заданном M_y, т.е. определить необходимую точность измерений.

Дата добавления: 2014-09-08; просмотров: 753; Нарушение авторских прав

Мы поможем в написании ваших работ!