Весовая функция

Для оценки точности уравненных величин составляют весовую функцию. Это математическое выражение оцениваемой величины (координаты, отметки и т.п.) в виде функции уравненных результатов измерений

F = F(y₁ + ν₁, y₂ + ν₂, ..., y_n + ν_n). (8)

Весовую функцию приводят к линейному виду разложением в ряд Тейлора

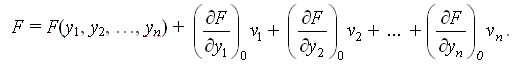
Обозначают

F(у₁, у₂, ..., у_n) = f₀ - постоянная (не вычисляется).

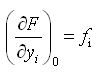- коэффициенты функции.

F = f₀ + f₁ν₁ + f₂ν₂ + ... + f_nν_n = f₀ + F_1n^ТV_n1. (9)

- весовая функция в линейном виде,

где 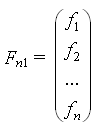- вектор коэффициентов функции.

Дата добавления: 2014-09-08; просмотров: 502; Нарушение авторских прав

Мы поможем в написании ваших работ!