Нормальные уравнения коррелат

Систему (7) условных уравнений поправок решают под условием (5) CНК

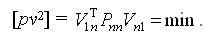
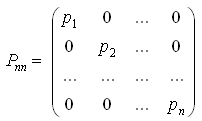- матрица весов результатов измерений.

Используют метод Лагранжа с неопределенными множителями, называемыми в геодезии коррелатами.

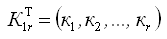- вектор коррелат.

Решение приводит к образованию системы нормальных уравнений коррелат

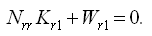(10)

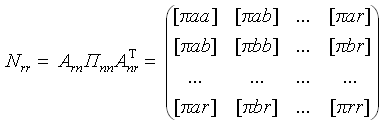- матрица коэффициентов нормальных уравнений. Коэффициенты, стоящие на главной диагонали, называются квадратичными. Они всегда положительны. Остальные коэффициенты неквадратичные.

π_i = 1/p_i - обратный вес результата измерения.

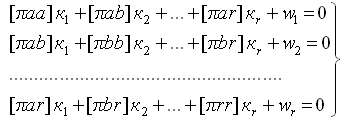(11)

- нормальные уравнения коррелат.

Из решения нормальных уравнений находят коррелаты к₁, к₂, ..., к_r, а затем поправки к результатам измерений по формуле:

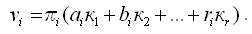(12)

После этого вычисляют уравненные значения результатов измерений

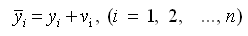(13)

и делают контроль уравнивания подстановкой уравненных измерений в условные уравнения связи, невязок не должно быть:

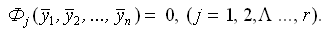(14)

Если измерения равноточные, вес измерения равен единице, p_i = π_i = 1, матрицы весов и обратных весов единичные P_nn = П_nn = E.

Дата добавления: 2014-09-08; просмотров: 427; Нарушение авторских прав

Мы поможем в написании ваших работ!