Критериальные уравнения массоотдачи

Поскольку аналитическое решение системы дифференциальных уравнений массообмена в общем виде невозможно, а при введении упрощающих предпосылок такие решения не гарантируют достоверности результатов, то большинство практических задач решается с использованием экспериментальных данных о процессе, обработанных с применением теории подобия.

Применяя метод масштабных преобразований к уравнению (9.5) и действуя так же, как при получении критерия Нуссельта, нетрудно получить следующий безразмерный комплекс, в обобщенном виде характеризующий интенсивность

процесса массоотдачи

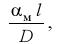
который называют массообменным числом Нуссельта N_uм. Здесь l – определяющий размер, выбираемый в каждом конкретном случае из условий однозначности. В качестве его принимается такой линейный размер, который существенн

влияет на массоотдачу.

При таком же анализе других дифференциальных уравнений можно получить и другие массообменные критерии, а так же критерии теплового и гидромеханического подобия, такие как Re и Gr. Определенная комбинация из этих критериев характеризует в обобщенном виде особенности теплофизических свойств мигрирующего компонента и ее называют массообменным критерием Прандтля

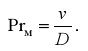
При описании неустановившихся процессов и нестационарных полей используется массообменный критерий Фурье

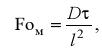
отображающий в безразмерном виде текущее время. Равенство значений этого критерия у двух подобных явлений означает, что они рассматриваются в сходственных состояниях.

Критерий N_uм является определяемым, остальные – определяющими, и критериальное уравнение массоотдачи в общем виде представляется зависимостью

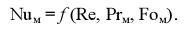
Исходя из отмеченной выше аналогии, можно доказать, что если для расчета теплоотдачи было получено ритериальное уравнение в виде

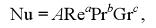
то массотдачу можно рассчитывать по аналогичной формуле с соответствующей заменой критериев

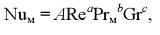(9.6)

где A, a, b и с – одни и те же опытные константы. Например, теплоотдачу при турбулентном течении теплоносителя в трубах рассчитывают по критериальному уравнению

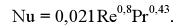
На основании аналогии для массоотдачи от слоя жидкости, равномерно покрывающего внутреннюю поверхность трубы, к турбулентному потоку парогазовой смеси можно записать следующее критериальное уравнение

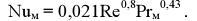
Сопоставление результатов, рассчитанных по этой формуле, с результатами экспериментальных измерений коэффициента массоотдачи показывает их приемлемое совпадение (расхождение в ± 20 % считается допустимым).

Однако обычно значения A, a, b и с в формуле (9.6) определяют путем соответствующей обработки экспериментальных данных по массоотдаче. Так, для расчета массоотдачи при сушке гранул в продуваемом слое рекомендуется следующее критериальное уравнение

где G_u = (T_п – T_мт) / T_п – так называемый критерий Гухмана, отражающий влияние интенсивности испарения на массоотдачу, T_п – абсолютная температура поверхности гранул; T_мт – абсолютная температура мокрого термометра, установленного вне пограничного слоя. Определяющий размер здесь – диаметр гранулы d. Для расчетов массообмена при испарении с плоской поверхности жидкости при вынужденном движении влажного газа А. В. Нестеренко предложено следующее критериальное уравнение

где А = 0,83 и а = 0,53 при Re 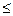120, А = 0,49 и а = 0,61 при Re = 3150 … 2200 и А = 0,0248 и а = 0,9 при Re = (0,22 … 3,15)10⁵ . В качестве определяющего размера здесь принимается длина поверхности вдоль по потоку смеси.

Дата добавления: 2014-03-11; просмотров: 1147; Нарушение авторских прав

Мы поможем в написании ваших работ!