Случайные процессы

11.1.Характеристики случайных процессов

Процессы, рассматриваемые в теории связи, могут быть детерминированными или случайными.

Детерминированные процессы - это процессы, течение которых во времени известно заранее и абсолютно точно.

Например, гармонический сигнал U(t) = U_mcos(w₀t+j₀), где U_m,, w₀, j₀ - заданы.

Это простейшая модель информационного сигнала, но она оказывается очень не точной для современных систем связи, дает большие погрешности в расчетах. Поэтому вводится новая модель, более сложная - случайные процессы (СП). Случайные процессы таковы, что их течение во времени заранее точно предсказать невозможно.

Пример СП - тепловой шум x(t).

Процесс случайный, т.к. мы не знаем его полностью. СП описывается своими реализациями, т.е. конкретными образцами.

Совокупность реализаций образует ансамбль (полная, но очень сложная характеристика СП).

Функция распределения вероятностей СП (ФРВ).

Функция распределения вероятностей обозначается F(x), характеризует вероятность того, что случайный процесс в некоторый момент времени t₁ принимает значение меньшее x₁ . Полное обозначение одномерной ФРВ

F(x₁ ,t₁ ) = P(x<x₁ , t=t₁ )

Двумерная ФРВ.

F₂ (x₁ t₁ ,x₂t₂) = P (x<x₁, t=t₁ ,x<x₂;t=t₂)

Наиболее полная характеристика n- мерная ФРВ:

F_n (x₁t₁...x_nt_n) = P (x<x₁;t<t₁; ... x<x_n;t=t_n)t

Функция плотности вероятностей случайного процесса ( ФПВ)

В простейшем случае одномерная ФПВ равна:

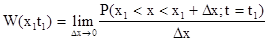
Одномерная ФПВ равна пределу отношения вероятности попадания случайного процесса в интервал от x₁ до х₁+Dх, при t= t₁, к Dх при Dх стремящемся к нулю.

Наиболее полной характеристикой является n - мерная ФПВ.

ФРВ и ФПВ связаны друг с другом . ФПВ - это первая производная ФРВ по х_1, Соответственно, ФРВ равна интегралу от -¥ до х₁ от ФПВ:_.

: F(x₁t₁) =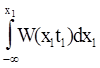

Условие нормировки :

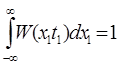
Числовые характеристики случайного процесса .

Среднее значение ( математическое ожидание или первый начальный момент)

m₁ =`x =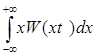

Физический смысл m₁ - это постоянная составляющая случайного процесса.

2.Второй начальный момент.

m₂ = `x² =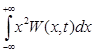

Физический смысл m₂ - это полная средняя мощность случайного процесса на единичном сопротивлении.

3.Дисперсия ( второй центральный момент )

s² = М₂ =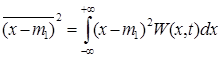

Физический смысл s² - это средняя мощность переменной составляющей случайного процесса на единичном сопротивлении.

Числовые характеристики связаны между собой:

s² = m₂ - m₁²

Стационарность.

1. Нестационарный случайный процесс - ФПВ и ФРВ зависят от начала отсчета времени.

2. Стационарный в узком смысле - ФПВ и ФРВ не зависят от начала отсчета времени.

3. Стационарный в широком смысле - одно- и двумерные ФПВ и ФРВ не зависят от начала отсчета времени.

Для стационарного случайного процесса m₁, m₂, s² - не зависят от времени.

Рассмотрим тепловой шум на выходе включенного усилителя:

x(t)

Рис.11.1.

t

нестационарный Стационарный

После включения усилитель прогревается и шум на его выходе - нестационарный. После "прогрева" шум будет стационарным процессом.

Эргодичность.

Случайный процесс называется эргодическим, если для него усреднение по времени одной реализации и усреднение по множеству реализаций дает один и тот же результат. Это свойство имеет большое значение на практике, т.к. усреднение по времени одной реализации технически реализовать проще, но оно не всегда дает истинный результат. Поэтому доказательство эргодичности процесса позволяет существенно упростить нахождение его характеристик.

11.2.Нормальный случайный процесс( гауссов процесс).

Процесс называется нормальным или гауссовым, если его одномерная ФПВ имеет вид:

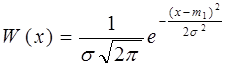
Графики нормальной ФПВ построены на рис. 11.2.:

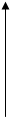W(x)

s₁ s₁ s₁

m₁<0 m₁=0 m₁>0 Рис.11.2.

s₂>s₁

m₁ - среднее значение случайного процесса . x

s² - дисперсия случайного процесса .

Свойства нормального случайного процесса .

1. W(x) ³ 0

2. Нормальная ФПВ симметрична относительно x = m₁

3. W(x) - max при х = m₁

4. Площадь под кривой W(x) равна 1.

5. При изменении m₁ форма кривой не меняется, но кривая смещается вдоль оси х.

6. Чем больше дисперсия s², тем кривая ниже и шире.

7. С вероятностью близкой к 1 (Р@0,997) мгновенные значения нормального случайного процесса лежат в пределах:

m₁ - 3s < x < m₁+3s

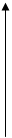W(x)

Рис.11.3.

3s 3s x

Если известна дисперсия и m₁, то рабочий участок ВАХ должен иметь протяженность m₁±3s.

8. ФРВ для нормального случайного процесса

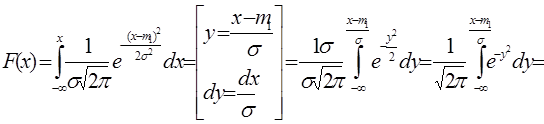
= F( 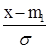) - табулированная функция (интеграл вероятности Лапласа)

F (0) = 0.5 F (-x) = 1- F(x)

F(3.9) = 0.99995 F (-¥) = 0; F(¥) = 1.

ФРВдля нормального процесса имеет вид:

F 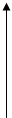(x)

1

0.5 Рис.11.4.

0m₁x

11.3.ФПВ и ФРВ для гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс в виде гармонического колебания со случайной начальной фазой:

X(t) = Asin ( wt + j )

j - случайная величина, равномерно распределенная на интервале ± p, т.е. ФПВ мгновенных значений фазы , показанная на рис.11.5 равна:

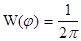; |x| £ p

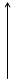W(j)

1/2p

Рис.11.5.

-p 0 p j

Вычислим среднее значение j:

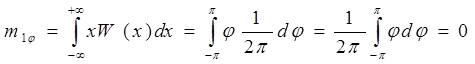
Вычислим дисперсию:

ФПВ мгновенных значений x гармонического колебания со случайной фазой, изображенная на рис. 11.6, имеет вид:

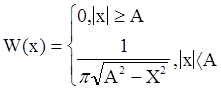
W(x)

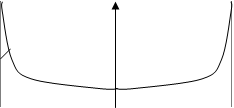
Рис.11.6.

-A 0 A x

Чем больше А, тем кривая ниже и шире. Заштрихованная площадь равна единице. Это площадь под кривой W(x) (условие нормировки)..

ФРВ мгновенных значений для гармонического колебания со случайной фазой:

X(t) = Asin ( wt + j )

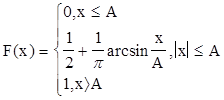
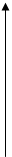F(x)

1

0.5

Рис.11.7.

-A 0 A x

11.4.ФПВ для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс z(t), равный:

Z(t) = x(t) + Asin (wt+ j)

где x(t) - нормальный случайный процесс;

Asin (wt+ j) - гармоническое колебание со случайной начальной фазой.

W(z) в этом случае находится сверткой.

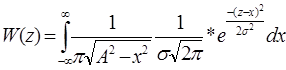
Вид ФПВ, т.е. W(z) зависит от параметра:

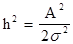
W(z)

h²=0 h²=¥

h²= 6

Рис.10.8.

0 z

h² = 0 - нормальный случайный процесс (чистый шум).

h² ® ¥ - одно гармоническое колебание.

11.5.Огибающая и фаза узкополосного случайного процесса.

Случайный процесс y(t) = U_m(t) cos ( w₀t+j(t) ) называется узкополосным, если его ширина спектра значительно меньше, чем средняя частота w₀.

U_m(t) - огибающая случайного процесса (случайная амплитуда) на рис.11.9;

j(t) - фаза случайного процесса.

Для нормального случайного процесса фаза j(t) распределена равномерно (см. выше).

u(t) Um(t)

Рис.11.9.

t

Огибающая нормального случайного процесса Um(t) распределена по закону Релея:

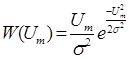; U_m ³ 0

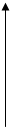W(Um)

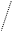
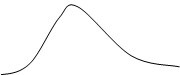з-н Релея

з-н Райса Рис.11.10.

0 Um

Если узкополосный случайный процесс есть сумма нормального шума и гармонического колебания с амплитудой А, то его огибающая распределена по обобщенному закону Релея (закон Райса):

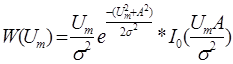закон Райса.

I₀(.) - функция Бесселя от мнимого аргумента.

11.6.ФПВ и ФРВ для дискретных случайных процессов.

Дискретные случайные процессы принимают с определенной вероятностью значения, отличающиеся одно от другого на конечную величину. Вероятность таких значений – число не равное 0.

Рассмотрим реализацию дискретного случайного процесса.

x(t)

а

T₁

Т₂ t Рис.11.11

b

T₁+T₂=T

Для эргодического стационарного случайного процесса усреднение по множеству реализаций эквивалентно усреднению по времени одной реализации.

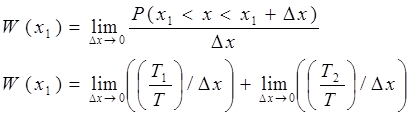
T₁/T - вероятность того, что случайный процесс принимает

значение а.

T₂/T - вероятность того, что случайный процесс принимает

значение b.

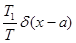ФПВзаданного случайного процесса в соответствии с полученным выражением показана на рис.11.12:

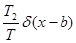W(x)

Рис.11.12.

b 0 a x

 

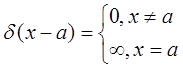
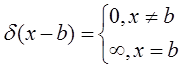
ФРВ для случайного процесса принимающего 2 значения x=a и x=b имеет вид:

 

 

 

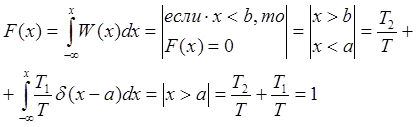
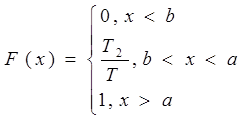
F(x)

 

1

 

T₂/T₁

Рис.11.13.

 

t

b a

 

Вычислим среднее значение двоичного дискретного случайного процесса, принимающего 2 значения:

x=a c вероятностью T₁/T, x=b c вероятностью T₂/T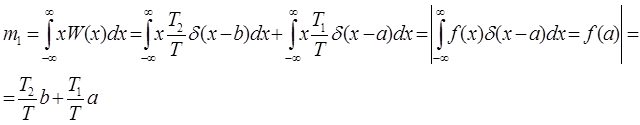

 

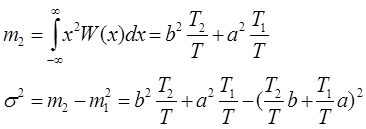
11.7.Нелинейные безынерционные преобразования случайного процесса.

 

Нелинейное преобразование:

y(t)=f[x(t)] – называется безынерционным, если y(t_k) в момент времени t_k зависит только от x(t_k).

ФПВ для процесса y на выходе:

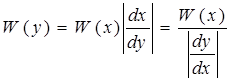
Пусть характеристика нелинейного элемента может быть аппроксимирована линейно-ломаными.

 

y

 

Рис.11.14

b

 

-a a x

-b

 

 

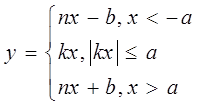
Это нелинейное устройство называется ограничителем.

Пусть на входе ограничителя действует нормальный случайный процесс с нулевым средним m_1x=0.

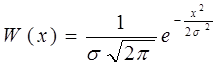
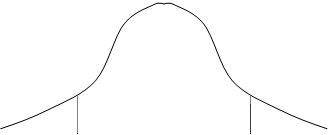
ФПВ процесса x нарисована на рис.11.15 (верхний рисунок).

Рассчитаем ФПВ процесса y:

1. Пусть 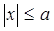у=kx (k>1)

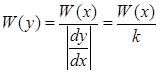Подставим в W(x) вместо x, y/k, тогда

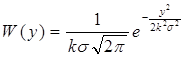
На интервале 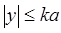ФПВ для у будет нормальной, со средним значением m_1y=0, но дисперсия y, т.е. .

 

 

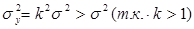W(x)

 

 

 

x

-a a

W(y)

 

 

Рис.11.15.

 

-ka 0 ka y

 

 

2. Пусть:

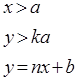
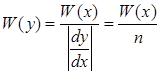
Выражаем x через у, т.е.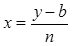

Это нормальная ФПВ со средним значением b и дисперсией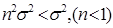

 

 

3.Пусть:

 

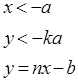
Это нормальная ФПВ, m₁= -b и дисперсия .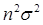

ФПВ процесса y дана на рис.11.15 (нижний рисунок).

11.8.ФПВ процесса на выходе идеализированного ограничителя.

Такой ограничитель имеет горизонтальные участки насыщения.

 

 

 

 

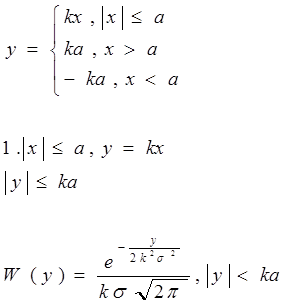
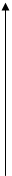W(y)

 

P(x<-a)d(y+ka) P(x>a)d(y-ka)

Рис.11.16.

 

-ka 0 ka y

 

11.9.ФПВ процесса на выходе идеального ограничителя.

Характеристика идеального ограничителя показана на рис.11.17.

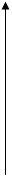y

ka Рис.11.17.

x

-ka

 

Процесс на выходе идеального ограничителя y - имеет только два значения : ка и –ка. Т.к. вероятность положительных и отрицательных значений х равна 0.5, то вероятность того, что y принимает значения +ka или -ka также равна 0.5. Поэтому, выполняя расчеты, как в предыдущем случае, получим, что ФПВ процесса y вырождается в две дельта-функции в точках y=-ka и y=ka (рис.11.18):

W(y)

 

 

0,5 d(y+ka) 0,5 d(y-ka)

Рис.11.18.

 

-ka 0 ka y

 

 

11.10.Линейные (инерционные) преобразования случайного процесса.

Дата добавления: 2014-09-08; просмотров: 610; Нарушение авторских прав

Мы поможем в написании ваших работ!