
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Показатели тесноты связи. Эмпирическое корреляционное отношение, индекс корреляции, коэффициент детерминации, линейный коэффициент корреляции
Коэффициент корреляции является полноценным показателем тесноты связи лишь в случае линейной зависимости между переменными. Однако часто возникает необходимость в достоверном показателе интенсивности связи при любой форме зависимости.
Для получения такого показателя вспомним правило сложения дисперсий 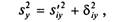 (1)
(1)
где S2y— общая дисперсия переменной
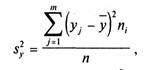 (2)
(2)
S’2iy — средняя групповых дисперсий Sу , или остаточная дисперсия —
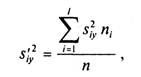 (3)
(3)
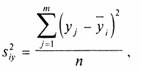 (4)
(4)
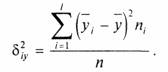 (5)
(5)
Остаточной дисперсией измеряют ту часть колеблемости Y, которая возникает из-за изменчивости неучтенных факторов, не зависящих от X.
Межгрупповая дисперсия выражает ту часть вариации Y, которая обусловлена изменчивостью X.
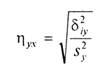 (6)
(6)
Величина получила название эмпирическогокорреляционного отношения Y по X. Чем теснее связь, тем большее влияние на вариацию переменной доказывает изменчивость X по сравнению с неучтенными факторами, тем выше ηyx.
Величина η2ух, называемая эмпирическим коэффициентом детерминации, показывает, какая часть общей вариации Y обусловлена вариацией X. Аналогично вводится эмпирическое корреляционное отношение X по Y.
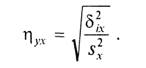 (7)
(7)
Отметим основные свойства корреляционных отношений (при достаточно большом объеме выборки п):
1. Корреляционное отношение есть неотрицательная величина, не превосходящая 1: 0≤η≤ 1.
2. Если η = 0, то корреляционная связь отсутствует.
3. Если η= 1, то между переменными существует функциональная зависимость.
4. ηxy≠ ηxy т.е. в отличие от коэффициента корреляции r (для которого ryx = rxy = r ) при вычислении корреляционного отношения существенно, какую переменную считать независимой, а какую — зависимой.

 Эмпирическое корреляционное отношение ηxy является показателем рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения yi . Однако в связи с тем, что закономерное изменение у, нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, Rxy преувеличивает тесноту связи. Поэтому наряду с ηxy рассматривается показатель тесноты связи Ryx, характеризующий рассеяние точек корреляционного поля относительно линии регрессии ух.
Эмпирическое корреляционное отношение ηxy является показателем рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения yi . Однако в связи с тем, что закономерное изменение у, нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, Rxy преувеличивает тесноту связи. Поэтому наряду с ηxy рассматривается показатель тесноты связи Ryx, характеризующий рассеяние точек корреляционного поля относительно линии регрессии ух.
Показатель Ryx получил название теоретического корреляционного отношения или индекса корреляции Y по X
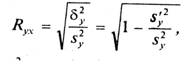 (8)
(8)
где дисперсии δ2у и s’y2 определяются по (2) - (4), в которых групповые средние yi, заменены условными средними ухi, вычисленными по уравнению регрессии. Подобно Ryx вводится и индекс корреляции X по Y
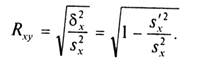 (9)
(9)
Достоинством рассмотренных показателей η и R является то, что они могут быть вычислены при любой форме связи между переменными. Хотя η и завышает тесноту связи по сравнению с R, но для его вычисления не нужно знать уравнение регрессии. Корреляционные отношения η и R связаны с коэффициентом корреляции r следующим образом:
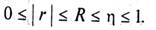 (10)
(10)
Покажем, что в случае линейной модели, т.е. зависимости

 ух - у = byx (x - х), индекс корреляции Rxy равен коэффициенту корреляции r (по абсолютной величине): Ryx = |r| (или Ryx= |r| ), для простоты ni= 1. По формуле (8)
ух - у = byx (x - х), индекс корреляции Rxy равен коэффициенту корреляции r (по абсолютной величине): Ryx = |r| (или Ryx= |r| ), для простоты ni= 1. По формуле (8)
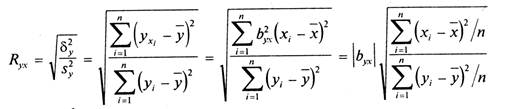

 (так как из уравнения регрессии yxi-y=byx(xi-x)
(так как из уравнения регрессии yxi-y=byx(xi-x)
Теперь, учитывая формулы дисперсии, коэффициентов регрессии и корреляции, получим:
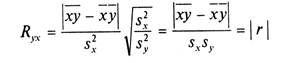 (11)
(11)
Коэффициент индекса корреляции показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной.Чем ближе индекс корреляции к 1, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия описывает зависимость переменных.
Проверка значимости корреляционного отношения η основана на том, что статистика
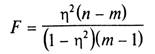 (12)
(12)
(где т — число интервалов по группировочному признаку) имеет F-распределение Фишера – Снедекора с к1=т-1 и k2=n – т степенями свободы. Поэтому ηзначимо отличается от нуля, если F >Fa,k1,k2, где F a,k1,k2 - табличное значение F-критерия на уровне значимости α при числе степеней свободы к1= т – 1 и к2= п – т.
Индекс корреляции R двух переменных значим, если значение статистики:
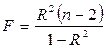 (13)
(13)
больше табличного F a,k1,k2, где к1=1 и k2 = n – 2.
Вариант XVII
Задача № 1.
Произведите группировку магазинов по признаку стоимость основных фондов, образовав при этом, пять групп с равными интервалами. Рассчитайте по каждой группе численность продавцов и размер торговой площади. Результаты группировки представьте в табличной форме и сформулируйте выводы.
Решение:
Расставим исходные данные (Табл.1) в порядке возрастания стоимости основных фондов. В результате получим Таблицу 2.
| Таблица 1 | Таблица 2 | |||||||
| Номер магазина | Стоимость основных фондов (среднегодовая) (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) | № магазина | Стоимость основных фондов (среднегодовая) (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) | |
| 6,3 | 2,3 | |||||||
| 5,7 | 2,8 | |||||||
| 5,0 | ||||||||
| 6,7 | ||||||||
| 6,5 | 4,1 | |||||||
| 4,8 | 4,6 | |||||||
| 6,8 | 4,8 | |||||||
| 3,0 | ||||||||
| 6,9 | 5,7 | |||||||
| 2,8 | 6,3 | |||||||
| 8,2 | 6,5 | |||||||
| 3,0 | 6,7 | |||||||
| 4,1 | 6,8 | |||||||
| 2,3 | 6,9 | |||||||
| 4,6 | 8,2 |
Ширина интервала группировки
h=(xmax – xmin)/5 = (8,2–2,3)/5=1,18.
В результате получим группы в интервалах:
| Группы: | Верхняя граница | Нижняя граница | Число магазинов |
| 1 группа | 2,3 | 3,48 | |
| 2 группа | 3,48 | 4,66 | |
| 3 группа | 4,66 | 5,84 | |
| 4 группа | 5,84 | 7,02 | |
| 5 группа | 7,02 | 8,2 |
Для каждой группы рассчитаем размер торговой площади и численность продавцов. Результаты расчетов запишем в таблицу:
| Таблица 3 | |||
| Стоимость основных фондов (среднегодовая) (млн. руб.) | Число магазинов | Численность продавцов (чел.) | Торговая площадь (м2) |
| 2,3–3,48 | |||
| 3,48–4,66 | |||
| 4,66–5,84 | |||
| 5,84–7,02 | |||
| 7,02–8,2 |
Выводы:
1. По стоимости основных фондов магазины распределены неравномерною
2. Число продавцов и торговая площадь в группе пропорционально размеру группы.
Задача № 2.
Исходные данные
| Стоимость основных фондов (среднегодовая) (млн. руб.) | Число магазинов |
| 2,3–3,48 | |
| 3,48–4,66 | |
| 4,66–5,84 | |
| 5,84–7,02 | |
| 7,02–8,2 |
Для вычисления статистических характеристик исходного интервального ряда необходимо выбрать некоторое среднее значения xi для каждого i-го интервала. Обычно это середина ряда. Поэтому получаем следующую таблицу:
| Средняя стоимость основных фондов (среднегодовая) (млн. руб.), xi | Число магазинов, ni |
| 2,89 | |
| 4,07 | |
| 5,25 | |
| 6,43 | |
| 7,61 |
Тогда среднее число продавцов: 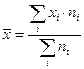 ; Дисперсия:
; Дисперсия:  ;
;
Среднее квадратическое отклонение: 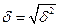 Коэффициент вариации:
Коэффициент вариации: 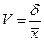
Для расчета составим таблицу (в пятом столбце рассчитываем накопленную частоту):
| Средняя стоимость основных фондов (среднегодовая) (млн. руб.), xi | Число магазинов, ni | xi·ni | ni·(xi-xср)2 | 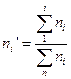
|
| 1 | 2 | 3 | 4 | 5 |
| 2,89 | 11,56 | 18,05 | 26,7% | |
| 4,07 | 8,14 | 1,78 | 40,0% | |
| 5,25 | 15,75 | 0,17 | 60,0% | |
| 6,43 | 32,15 | 10,03 | 93,3% | |
| 7,61 | 7,61 | 6,74 | 100,0% | |
| всего: | 75,21 | 36,76 |
Средняя стоимость ОФ: 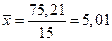 чел.; Дисперсия:
чел.; Дисперсия: 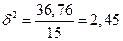 ;
;
Среднее квадратическое отклонение: 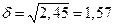 чел.
чел.
Коэффициент вариации: 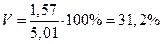
Мода
Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. В нашем случае это четвёртый интервал с частотой (5).
Модальное значение: 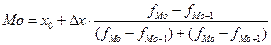
где x0 — нижняя граница модального интервала (x0 = 5,84) ;
fМо — частота в модальном интервале (5);
fМо–1 — частота в предыдущем интервале (3);
fМо+1 — частота в следующем интервале за модальным (1);
Dx — величина интервала (1,18)
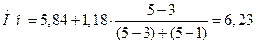 млн. руб.
млн. руб.
Мода равна 60 млн. руб.
Медиана
Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. В нашем случае это третий интервал:
Медианное значение: 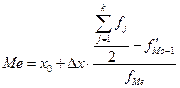
где x0 — нижняя граница медианного интервала (x0 =5,25);
f’Мe-1 — накопленная частота в интервале, предшествующем медианному; (f’Мe-1 = 4 + 2 = 6);
fМе — частота в медианном интервале (fМе = 3);
k — число групп;
Dx — величина интервала (1,18)
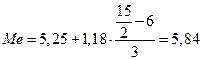 млн. руб.
млн. руб.
Медиана равна 5,84 млн. руб.
| <== предыдущая страница | | | следующая страница ==> |
| Интерактивные задания | | | КОНТРОЛЬНАЯ РАБОТА №2 (по темам №3 и№4) |
Дата добавления: 2014-09-08; просмотров: 1156; Нарушение авторских прав

Мы поможем в написании ваших работ!