Нормальная кривая

График плотности нормального распределения называется нормальной кривой (кривой Гаусса). Исследуем функцию 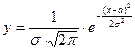методами дифференцирующего исчисления.

1. Очевидно, что функция определена на всей оси ОХ.

2. При всех значениях функции принимает положительное значение.

3. Предел функции при неограниченном возрастании 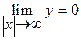, т.е. ось ОХ служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум .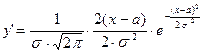

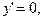если x=a.

Если x<a, 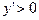– функция возрастает, если x>a, 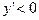– функция убывает. Следовательно в точке x=a функция имеет максимум .

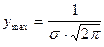5. График функции симметричен относительно прямой x=a.

6. Исследуем функцию на точки перегиба =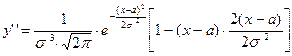

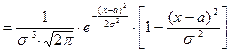
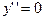при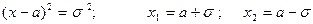

Можно проверить, что при переходе через эти точки вторая производная меняет знак. В обеих этих точках значение функции равно: 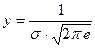. Таким образом точки графика с координатам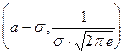и и 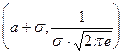– точки перегиба.

Выясним, как влияют на форму и расположение нормальной кривой :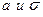

1. Измение величины 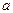(мат. ожидание) не изменяет форму нормальной кривой, а приводит лишь к сдвигу по оси ОХ (вправо, если 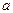возрастает, влево, если 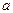убывает).

2. С возрастанием 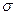максимальная ордината нормальной кривой убывает, а сама кривая становится полной (сжимается к оси ОХ). При убывании 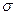кривая становится островершинной и растягивается вдоль OY.

При любых значениях 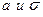площадь, ограниченная нормальной кривой и ОХ равна 1

Дата добавления: 2014-02-26; просмотров: 698; Нарушение авторских прав

Мы поможем в написании ваших работ!