
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сложение и вычитание векторов
 Определение 1.Пусть даны векторы
Определение 1.Пусть даны векторы  и
и  .От точки А отложим вектор
.От точки А отложим вектор  , а от конца направленного отрезка
, а от конца направленного отрезка 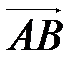 отложим вектор
отложим вектор  . Вектор
. Вектор 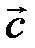 , определенный направленным отрезком
, определенный направленным отрезком  , называется суммой векторов
, называется суммой векторов  и
и  :
: 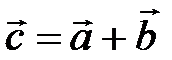 .
.

 Построение суммы векторов
Построение суммы векторов  и
и 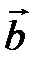 показано на рисунке 4. Из определения 1 следует, что для любых трех точек А, В и С выполнено равенство:
показано на рисунке 4. Из определения 1 следует, что для любых трех точек А, В и С выполнено равенство:  , Поэтому такой способ сложения векторов часто называют правилом треугольника. Наряду с ним используется еще один способ определения суммы векторов - правило параллелограмма. Если
, Поэтому такой способ сложения векторов часто называют правилом треугольника. Наряду с ним используется еще один способ определения суммы векторов - правило параллелограмма. Если  и
и 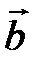 - два неколлинеарных вектора, то для построения суммы
- два неколлинеарных вектора, то для построения суммы  по правилу параллелограмма отложим их от одной точки:
по правилу параллелограмма отложим их от одной точки:  Затем треугольник ABD достроим до параллелограмма ABCD. Искомая сумма равна вектору
Затем треугольник ABD достроим до параллелограмма ABCD. Искомая сумма равна вектору  (рис. 5). Для обоснования корректности определения 1 следует проверить, что сумма векторов
(рис. 5). Для обоснования корректности определения 1 следует проверить, что сумма векторов  и
и  не зависит от выбора начальной точки А. Действительно, возьмем две точки А и А
не зависит от выбора начальной точки А. Действительно, возьмем две точки А и А  , отложим от них же вектор
, отложим от них же вектор 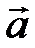 :
: 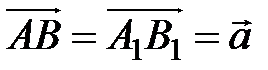 , от точек B и B
, от точек B и B  отложим вектор
отложим вектор 
 :
:  (рис. 6). Так как
(рис. 6). Так как  , то
, то  Аналогично, из равенства
Аналогично, из равенства  вытекает
вытекает  . Следовательно,
. Следовательно,  , откуда получим, что
, откуда получим, что  .
.
Рассмотрим свойства операции сложения векторов.
 Свойство 1.Для любых векторов
Свойство 1.Для любых векторов  и
и  справедливо равенство:
справедливо равенство: 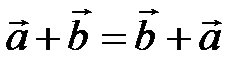 . (свойство коммутативности).
. (свойство коммутативности).
Доказательство.Отложим от точки А вектор  , а от точки В вектор
, а от точки В вектор  . Тогда
. Тогда  (рис. 7). Теперь отложим от точки А вектор
(рис. 7). Теперь отложим от точки А вектор 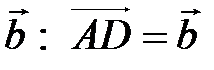 , Так как направленные отрезки
, Так как направленные отрезки  и
и  равны друг другу, то
равны друг другу, то  (см. свойство 3, § 1). Отсюда следует, что
(см. свойство 3, § 1). Отсюда следует, что  , т.е.
, т.е. 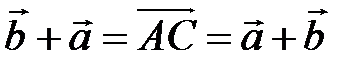 . Свойство доказано.
. Свойство доказано.
Свойство 2. Для любых векторов  и
и  выполнено равенство:
выполнено равенство:  (свойство ассоциативности).
(свойство ассоциативности).

 Доказательство. Отложим последовательно от точки А вектор
Доказательство. Отложим последовательно от точки А вектор  , от точки В вектор
, от точки В вектор 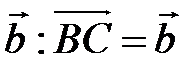 , а от точки С вектор
, а от точки С вектор  (рис. 8). Тогда
(рис. 8). Тогда 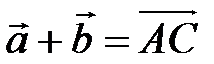 и из равенств
и из равенств  ,
, 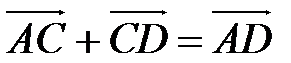 следует,
следует,  С другой стороны,
С другой стороны,  , поэтому
, поэтому 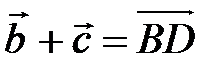 . Так как
. Так как 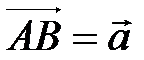 и
и 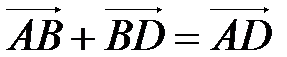 , то
, то  . Свойство доказано.
. Свойство доказано.
Свойство 2 позволяет определить сумму любого числа векторов  . Она равна результату последовательного суммирования
. Она равна результату последовательного суммирования  , к сумме первых двух векторов прибавляется третий, затем четвертый и т.д. Из свойства 1 вытекает, что результат суммирования любого числа векторов не зависит от порядка суммирования. На рисунке 9 изображен процесс построения суммы шести векторов.
, к сумме первых двух векторов прибавляется третий, затем четвертый и т.д. Из свойства 1 вытекает, что результат суммирования любого числа векторов не зависит от порядка суммирования. На рисунке 9 изображен процесс построения суммы шести векторов.
Свойство 3.Для любого вектора 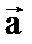 выполнено соотношение:
выполнено соотношение:  .
.
Доказательство.Отложим от точки А вектор  , а от точки В вектор
, а от точки В вектор 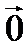 . Так как
. Так как  , то
, то  . Свойство доказано.
. Свойство доказано.
Свойство 4.Для любого вектора  его сумма с противоположным вектором
его сумма с противоположным вектором  равна нулевому вектору:
равна нулевому вектору:  .
.
Доказательство.Вектор  , противоположный
, противоположный  , имеет ту же длину, что и
, имеет ту же длину, что и  , но противоположное направление. Отложим от точки А вектор
, но противоположное направление. Отложим от точки А вектор  . Если от точки В отложить вектор
. Если от точки В отложить вектор  , то его конец совпадет с точкой А. Поэтому
, то его конец совпадет с точкой А. Поэтому  . Свойство доказано.
. Свойство доказано.
При суммировании векторов, вообще говоря, их модули не складываются. Действительно, возьмем два произвольных вектора  и
и  . Отложим от точки А вектор
. Отложим от точки А вектор  , а от точки В вектор
, а от точки В вектор  , получим:
, получим:  . Пусть векторы
. Пусть векторы  и
и  не коллинеарные. Тогда точки А, В и С лежат в вершинах треугольника. Исходя из неравенства треугольника получим
не коллинеарные. Тогда точки А, В и С лежат в вершинах треугольника. Исходя из неравенства треугольника получим  , т.е.
, т.е. 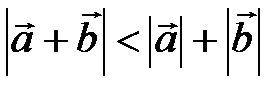 . Пусть теперь векторы
. Пусть теперь векторы  и
и  коллинеарные. Если они сонаправлены, то точка В лежит между А и С, поэтому
коллинеарные. Если они сонаправлены, то точка В лежит между А и С, поэтому  , т.е.
, т.е.  . Если они противоположно направлены, то точка В не лежит между А и С, тогда
. Если они противоположно направлены, то точка В не лежит между А и С, тогда 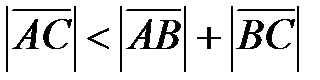 , т.е.
, т.е. 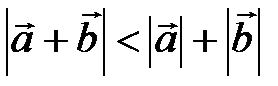 . Таким образом, нами доказано неравенство:
. Таким образом, нами доказано неравенство: 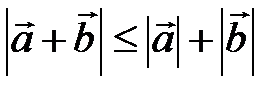 .
.
 Определение 2.Под разностью двух векторов
Определение 2.Под разностью двух векторов  понимается вектор
понимается вектор  , удовлетворяющий условию:
, удовлетворяющий условию: 
Пусть даны два вектора 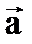 и
и  . Рассмотрим сумму вектора
. Рассмотрим сумму вектора  и вектор, противоположного
и вектор, противоположного 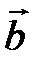 :
:  . Докажем, что
. Докажем, что 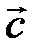
 удовлетворяет условию:
удовлетворяет условию:  . Используем свойства 3 и 4 операции сложения:
. Используем свойства 3 и 4 операции сложения: 
Можно найти разность  иначе. Для этого отложим векторы
иначе. Для этого отложим векторы  и
и  от одной точки A:
от одной точки A:  (рис. 10). Соединив концы C и B, выберем направление отрезка СВ от вычитаемого к уменьшаемому, т.е. от вектора
(рис. 10). Соединив концы C и B, выберем направление отрезка СВ от вычитаемого к уменьшаемому, т.е. от вектора  к вектору
к вектору  , от С к В. Так как
, от С к В. Так как  , то
, то 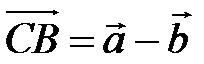 .
.
Для модуля разности двух векторов справедливы неравенства  . Проверьте их самостоятельно.
. Проверьте их самостоятельно.
| <== предыдущая страница | | | следующая страница ==> |
| Тестовый контроль. 3) исключают приемы постукивания | | | Основы химической термодинамики |
Дата добавления: 2014-09-26; просмотров: 601; Нарушение авторских прав

Мы поможем в написании ваших работ!