Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Основные формы записи комплексных векторов
Основные операции с комплексными числами
Рассмотрим запись комплексных векторов в показательной и алгебраической формах на комплексной плоскости в зависимости от угла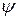 
и их величин.
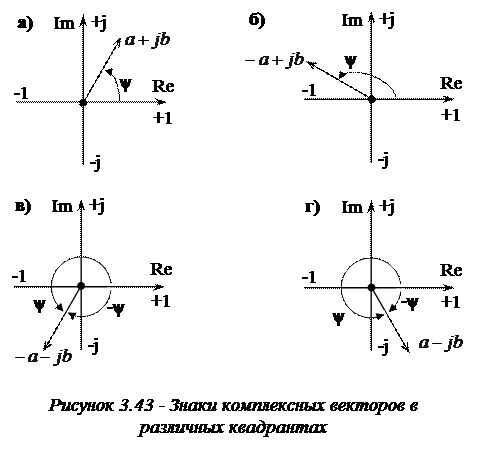
В зависимости от угла 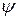, а следовательно его расположения в определенном квадранте, знаки действительной и мнимой части могут быть различными (рис. 3.43).
В I-м квадранте имеет место 
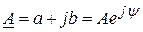(рис. 3.43,а) и 
.
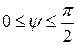В II-м квадранте имеет место 
(рис. 3.43,б) и 
.
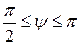В III-м квадранте имеет место 
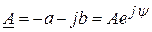(рис. 3.43,в) и 
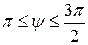. Аргумент 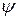в третьем квадранте рационально записывать со знаком ”
”. В этом случае, вектор откладывается по часовой стрелке со знаком ”-”.
Например, комплексный вектор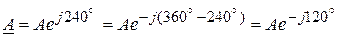 
.
 |
В IV-м квадранте имеет место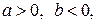 
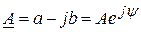(рис. 3.43,г) и 
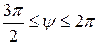. Аргумент 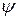в четвертом квадранте рационально записывать со знаком ””. В этом случае, вектор откладывается по часовой стрелке. Например, комплексный вектор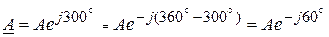 
.
В операциях с комплексными векторами используется понятие комплексно сопряженного вектора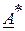 
(рис. 3.44). Для комплексного вектора 
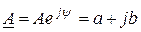сопряженный комплексный вектор равен 
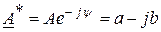. Комплексно сопряженный вектор может быть получен в показательной форме из комплексного вектора путем замены знака аргумента 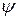на противоположный, либо заменой знака мнимой величины на противоположный в алгебраической форме.
 |
| <== предыдущая страница | | | следующая страница ==> |
| Понятие комплексных векторов | | | Основные операции с комплексными векторами |
Дата добавления: 2014-02-27; просмотров: 482; Нарушение авторских прав
Мы поможем в написании ваших работ!