Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Проекции поверхностей. Задание поверхности на чертеже
Поверхностью в геометрии называется граница, отделяющая геометрическое тело (цилиндр, конус, шар и т.д.) от внешнего пространства. На чертежах (эпюрах) изображают только точки и линии (прямые или кривые). Поэтому поверхность можно изобразить только тогда, когда она проецируется в линию или совокупность линий.
Поверхность может быть задана с помощью модели (обувная колодка, манекен и др.), с помощью уравнения, кинематически – как след движущейся в пространстве линии, и др. В начертательной геометрии принят кинематический способ образования поверхности. Можно сказать, что поверхность – это непрерывная совокупность последовательных положений движущейся в пространстве прямой или кривой линии. Линия, которая при своем движении образует поверхность, называется образующей.
2.4.1. Задание поверхности с помощью определителя. Для того, чтобы задать поверхность, достаточно задать образующую поверхности и определить закон, по которому она перемещается в пространстве. Законы движения образующих могут задаваться различно:
1) Образующая движется, пересекая какую-либо неподвижную линию, которая называется направляющей.
2) Образующая движется, пересекая две или три направляющие линии.
3) Образующая движется параллельно самой себе или параллельно некоторой плоскости, которая называется плоскостью параллелизма и др.
Образующая вместе с геометрическими фигурами, определяющими ее движение, а также закон ее движения составляют определитель поверхности. Можно сказать, что определитель поверхности представляет собой совокупность независимых параметров, однозначно задающих поверхность.
Определитель состоит из двух частей:
1) Геометрическая часть – фигуры (точки, линии, поверхности) подвижные и неподвижные, с помощью которых образуется поверхность.
2) Алгоритмическая часть – правило движения (закон движения) образующей по отношению к неподвижным фигурам определителя.
В ряде случаев образующая при своем движении может деформироваться, что тоже оговаривается в алгоритмической части определителя. Основанием к составлению определителя является анализ способа образования поверхности и ее основных свойств. Каждая поверхность может быть задана разными определителями.
Для примера рассмотрим определитель произвольной цилиндрической поверхности (рис. 2.34). Запись определителя имеет вид:
Ф(l, a) - цилиндрическая поверхность
(геометрическая часть) (алгоритмическая часть)
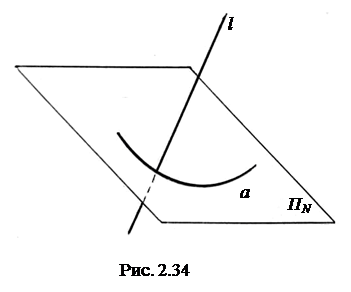 Эта запись дается совместно с чертежом. В записи геометрической части буквой Ф обозначается поверхность, буквой l – образующая, буквой а - направляющая. Форма и положение в пространстве образующей и направляющей определяются по чертежу.
Эта запись дается совместно с чертежом. В записи геометрической части буквой Ф обозначается поверхность, буквой l – образующая, буквой а - направляющая. Форма и положение в пространстве образующей и направляющей определяются по чертежу.
В записи алгоритми-ческой части дается название поверхности. Для поверх-ности с данным названием общеизвестно, какое движе-ние совершает l, образуя поверхность Ф. Но можно и подробно записать характер движения образующей. В нашем случае образующая l движется параллельно самой себе и все время пересекает направляющую а. Определитель вполне определяет поверхность, т.к. с его помощью можно построить ее проекции.
На рис. 2.35, а задан комплексный чертеж определителя цилиндрической поверхности Ф(l, a) и проекция А2 точки А, принадлежащей поверхности. Необходимо построить горизонтальную проекцию А1 точки А.
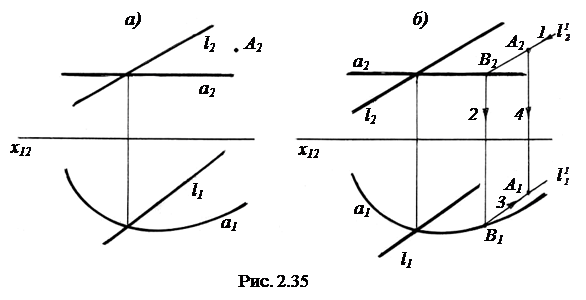
Зная алгоритмическую часть определителя, выполним следующие построения (рис. 2.35, б):
1) Через А2 параллельно l2 проводим 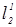 и находим фронтальную проекцию В2 точки пересечения
и находим фронтальную проекцию В2 точки пересечения 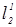 с а2 (этап 1). Этапы указаны стрелками.
с а2 (этап 1). Этапы указаны стрелками.
2) С помощью линии проекционной связи на а1 находим В1 (этап 2).
3) Через точку В1 проводим 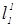 параллельно l1 (этап 3).
параллельно l1 (этап 3).
4) На  с помощью линии связи строим А1 (этап 4).
с помощью линии связи строим А1 (этап 4).
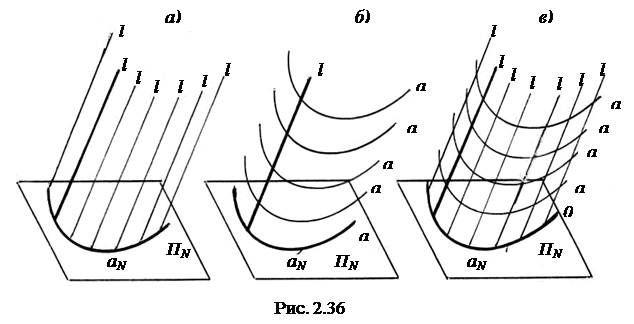
2.4.2. Каркас поверхности. Если построить некоторое количество образующих по описанному в алгоритме определителя способу, то получим каркас или сеть поверхности (рис. 2.36).
Изображенный на рис. 2.36, а каркас называется однопараметрическим, т.к. он состоит из линий, принадлежащих одному семейству. Это дискретный каркас, он состоит из конечного числа линий.
Можно представить себе и непрерывный каркас образующих. Непрерывный каркас – это множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит только одна линия каркаса.
На одной и той же поверхности, в зависимости от определителя, можно представить себе и другие каркасы. Если в определителе цилиндрической поверхности образующую и направляющую поменять местами и считать, что кривая а будет образующей, которая движется параллельно самой себе и все время пересекает направляющую l, то получится другой однопараметрический каркас (рис. 2.36, б).
Если на поверхности построить два каркаса, то получится двупараметрический каркас (рис. 2.36, в). Через каждую точку поверхности, заданной двупараметрическим каркасом, проходят две линии каркаса.
2.4.3. Задание поверхности, не имеющей определителя. Существуют незакономерные поверхности, к которым относятся манекен, обувная колодка, кузова автомобилей, фюзеляжи самолетов, корпуса морских и речных судов, рельеф земной поверхности и др. Такие поверхности называются графическими и задаются дискретным каркасом. Чаще всего линии этого каркаса представляют собой плоские кривые, параллельные какой-либо плоскости проекций. Если плоскости линий каркаса параллельны горизонтальной плоскости проекций, то такие линии называются горизонтальными.
2.4.4. Очерк поверхности. Линия пересечения проецирующей поверхности, огибающей заданную поверхность, с плоскостью проекций называется очерком поверхности. На рис. 2.37 показано проецирование сферы Т на плоскость П1. Множество горизонтально-проецирующих лучей, касательных к поверхности сферы, образуют огибающую горизонтально–проецирующую цилиндрическую поверхность Ф. Линия пересечения Ф и П1 представляет собой горизонтальный очерк поверхности – окружность а1.
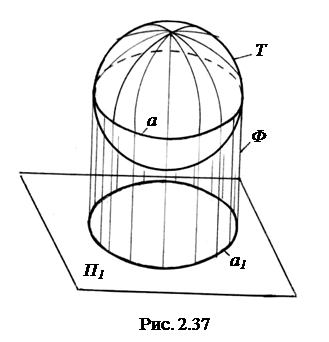 Очерковой линией повер-хности называется линия, по которой огибающая проеци-рующая поверхность касается данной поверхности. В нашем случае очерковой линией будет большая окружность сферы а (экватор).
Очерковой линией повер-хности называется линия, по которой огибающая проеци-рующая поверхность касается данной поверхности. В нашем случае очерковой линией будет большая окружность сферы а (экватор).
Изображения поверхнос-тей, заданных определителем, не всегда наглядны. Более наглядны изображения поверхностей с помощью очерков. Очерк поверхности почти всегда включает в себя ее определитель. При построении проекций точки, лежащей на поверхности, изображенной очерком, необходимо сначала выделить проекции определителя, а потом, пользуясь алгоритмом определителя, построить проекции точки.
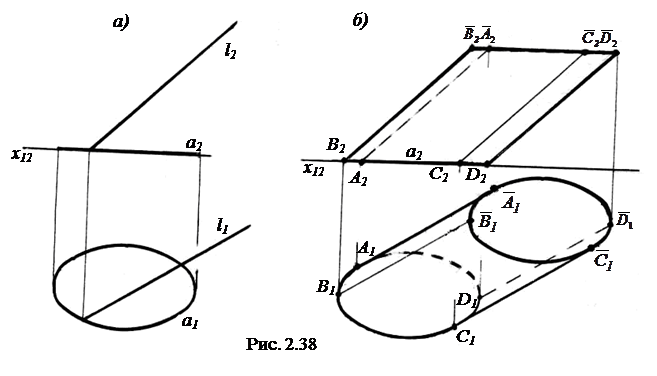
На рис. 2.38, а поверхность наклонного эллиптического цилиндра задана определителем, а на рис. 2.38, б очерком. Горизонтальный очерк представляет собой линию, состоящую из отрезков прямых и кривых 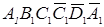 ; фронтальный очерк представляет собой параллелограмм
; фронтальный очерк представляет собой параллелограмм 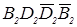 .
.
Образующие горизонтального очерка 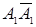 и
и 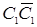 и образующие фронтального очерка
и образующие фронтального очерка 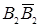 и
и 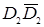 не совпадают друг с другом. Из проекций очерка можно выделить геометрическую часть определителя, которая будет состоять из эллипса
не совпадают друг с другом. Из проекций очерка можно выделить геометрическую часть определителя, которая будет состоять из эллипса 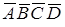 и какой-нибудь образующей, например
и какой-нибудь образующей, например 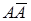 .
. 
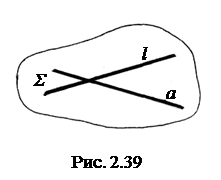 2.4.5. Проекции плоскостей. Плоскость можно рассматривать как частный случай поверхности. Плоскость Σ может быть образована за счет движения прямолинейной образующей l параллельно самой себе, при этом образующая пересекает все точки направляющей прямой а (рис. 2.39). Определитель плоскости в этом случае имеет вид: Σ(а, l).
2.4.5. Проекции плоскостей. Плоскость можно рассматривать как частный случай поверхности. Плоскость Σ может быть образована за счет движения прямолинейной образующей l параллельно самой себе, при этом образующая пересекает все точки направляющей прямой а (рис. 2.39). Определитель плоскости в этом случае имеет вид: Σ(а, l).
Из геометрии известно, что плоскости вполне определяются:
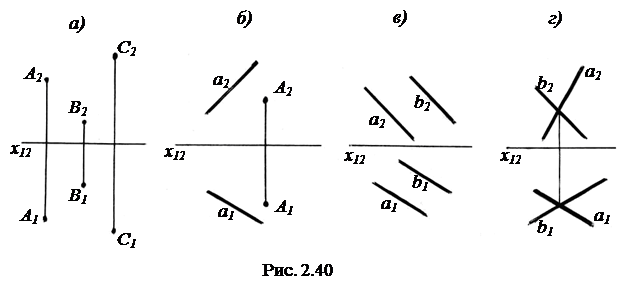
1) Тремя точками А, В и С, не лежащими на одной прямой (рис.2.40, а).
2) Прямой а и точкой А вне её (рис. 2.40, б).
3) Двумя параллельными прямыми а и b (рис. 2.40, в).
4) Двумя пересекающимися прямыми а и b (рис. 2.40, г).
Задание плоскости пересекающимися прямыми а и b (рис. 2.40, г) можно рассматривать, как универсальный способ задания плоскости, так как все остальные можно привести к нему. Так, например, если плоскость задана тремя точками А, В и С (рис. 2.40, а), то, соединяя точки А с В и В с С, получаем пересекающиеся прямые АВ и ВС.
2.4.6. Виды плоскостей по их расположению в пространстве. По расположению относительно плоскостей проекций плоскости можно разбить на три вида:
1) плоскости общего положения – плоскости, не параллельные и не перпендикулярные плоскостям проекций;
2) плоскости проецирующие – плоскости, перпендикулярные к какой-либо плоскости проекций;
3) плоскости уровня – плоскости, параллельные какой-либо одной плоскости проекций и перпендикулярные двум другим.
Рассмотрим некоторые особенности каждого из перечисленных видов плоскостей.
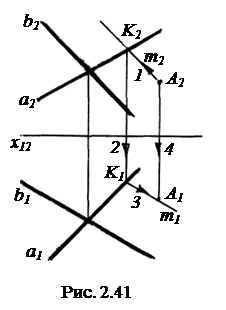 Плоскости общего положения. На рис. 2.40 изображены плоскости общего положения. Для этих плоскостей характерно, что задающие их элементы (точки, прямые и др.) ни на одной проекции не сливаются в прямую линию, т.е. не лежат на одной прямой.
Плоскости общего положения. На рис. 2.40 изображены плоскости общего положения. Для этих плоскостей характерно, что задающие их элементы (точки, прямые и др.) ни на одной проекции не сливаются в прямую линию, т.е. не лежат на одной прямой.
На рис. 2.41 задана плоскость Σ( 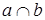 ) и одна проекция А2 точки А, принадлежащей плоскости Σ. Будем считать, что а – направляющая, а b - образующая плоскости Σ. Помня, что все образующие параллельны между собой и все пересекаются с направляющей, выполним следующие построения:
) и одна проекция А2 точки А, принадлежащей плоскости Σ. Будем считать, что а – направляющая, а b - образующая плоскости Σ. Помня, что все образующие параллельны между собой и все пересекаются с направляющей, выполним следующие построения:
1) Через точку А2 проведем проекцию образующей m2║b2 и построим точку К2 пересечения m2 с а2 (этап 1).
2) На линии связи и на а1 находим К1 (этап 2).
3) Через К1 проводим m1║b1 (этап 3).
4) С помощью линии связи на m1 находим А1 (этап 4).
В данном построении образующая m1, лежащая в плоскости Σ, строилась по точке и известному направлению. Однако при построении точки, лежащей в плоскости, можно воспользоваться не только образующей, лежащей в плоскости. На рис. 2.42 горизонтальная проекция точки А построена с помощью произвольной прямой. При этом выполнены построения:
1) Через заданную проекцию А2 проводим произвольную прямую m2 и, считая, что m лежит в плоскости Σ( 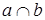 ), отмечаем точки ее пересечения К2 и М2 с а2 и b2 (этап 1).
), отмечаем точки ее пересечения К2 и М2 с а2 и b2 (этап 1).
2) Строим К1 и М1 на а1 и b1 с помощью линий связи (этап 2).
3) Соединим К1 и М1 и получим m1 (этап 3).
4) На m1 с помощью линии связи находим А1 (этап 4).
Очевидно, для того, чтобы в плоскости построить точку, необходимо в этой плоскости провести прямую и затем на прямой взять точку. При этом прямая расположена в плоскости, если она проходит через две точки, принадлежащие плоскости.
Проецирующие плоскости.Различают три вида проецирующих плоскостей:
1) Горизонтально-проецирующие, перпендикулярные П1.
2) Фронтально-проецирующие, перпендикулярные П2.
3) Профильно-проецирующие, перпендикулярные П3.
При изображении проецирующих плоскостей надо иметь в виду, что одноименная проекция такой плоскости всегда вырождается в прямую, как было показано ранее. Эта прямая называется главной проекцией или следом проецирующей плоскости; эту проекцию также называют вырожденной. Для того, чтобы отличать проецирующую плоскость от прямой, главную проекцию проецирующей плоскости на чертеже часто изображают с утолщением конца.
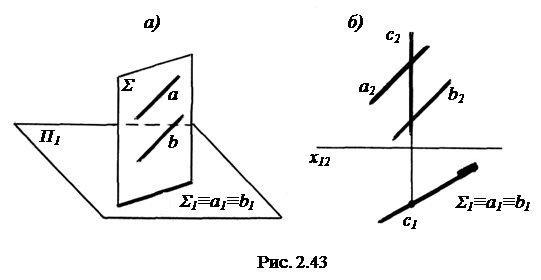
На рис. 2.43, а показано наглядное изображение произвольной горизонтально-проецирующей плоскости Σ (а║b) и ее главной проекции Σ1. Комплексный чертеж этой плоскости приведен на рис.2.43, б. На главную проекцию плоскости проецируются все точки, лежащие в плоскости.
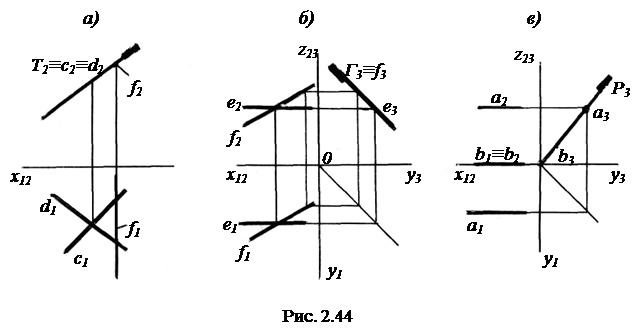
Фронтально-проецирующая плоскость Т(с 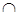 d) изображена на рис. 2.44, а, профильно-проецирующая плоскость Г (е
d) изображена на рис. 2.44, а, профильно-проецирующая плоскость Г (е 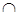 f) - на рис. 2.44, б и профильно-проецирующая плоскость Р (а ║ b ) - на рис. 2.44, в.
f) - на рис. 2.44, б и профильно-проецирующая плоскость Р (а ║ b ) - на рис. 2.44, в.
Благодаря проецирующему свойству прое 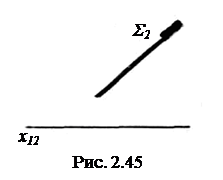 цирующие плоскости можно задавать одной своей главной проекцией (следом, вырожденной
цирующие плоскости можно задавать одной своей главной проекцией (следом, вырожденной 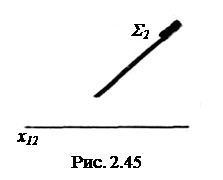 проекцией). На рис. 2.45 задана фронтально-проецирующая плоскость Σ.
проекцией). На рис. 2.45 задана фронтально-проецирующая плоскость Σ.
Из стереометрии известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой. Поэтому в каждой проецирующей плоскости можно построить одноименную проецирующую прямую. На рис. 2.43, б в плоскости Σ (а║b) построена горизонтально-проецирующая прямая с. На рис. 2.44, а в плоскости Т (с  d) построена фронтально-проецирующая прямая f .
d) построена фронтально-проецирующая прямая f .
В плоскостях Г (е  f) (рис. 2.44, б) и Р (а ║ b ) (рис. 2.44, в) есть прямые, перпендикулярные П3 . Следовательно, эти плоскости являются профильно-проецирующими. Таким образом, профильно-проецирующие плоскости можно задавать только проекциями на П1 и П2.
f) (рис. 2.44, б) и Р (а ║ b ) (рис. 2.44, в) есть прямые, перпендикулярные П3 . Следовательно, эти плоскости являются профильно-проецирующими. Таким образом, профильно-проецирующие плоскости можно задавать только проекциями на П1 и П2.
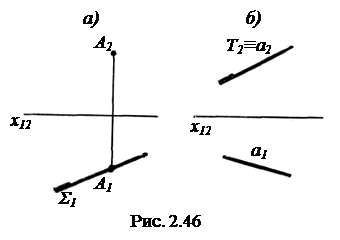 Вопрос о принадлежности точки и прямой к проецирующей плоскости решается проще, чем у плоскости общего положения. Проекция точки или прямой всегда находится в главной проекции плоскости, выродившейся в линию. Так, на рис.2.46, а показаны проекции точки А, а на рис. 2.46, б - прямой а, принадлежащих соответственно горизонтально- проецирующей плоскости Σ и фронтально-проецирующей плоскости Т.
Вопрос о принадлежности точки и прямой к проецирующей плоскости решается проще, чем у плоскости общего положения. Проекция точки или прямой всегда находится в главной проекции плоскости, выродившейся в линию. Так, на рис.2.46, а показаны проекции точки А, а на рис. 2.46, б - прямой а, принадлежащих соответственно горизонтально- проецирующей плоскости Σ и фронтально-проецирующей плоскости Т.
Плоскости уровня. Различают три вида плоскостей уровня:
1) Горизонтальная плоскость, параллельная П1 и перпендикулярная П2 и П3.
2) Фронтальная плоскость, параллельная П2 и перпендикулярная П1 и П3.
3) Профильная плоскость, параллельная П3 и перпендикулярная П1 и П2.
Плоскости уровня можно назвать дважды проецирующими, т. к. каждая из них перпендикулярна к двум плоскостям проекций.
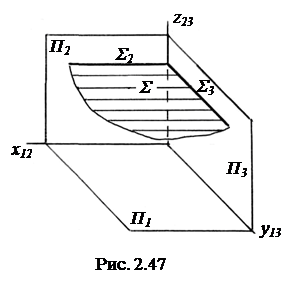 Из проецирующего свойства вытекает, что плоскости уровня проецируются в линии, каждая на двух плоскостях проекций. На рис. 2.47 дано наглядное изображение горизонтальной плоскости уровня Σ. Характерной особенностью чертежей плоскостей уровня является параллельность главной (вырожденной) проекции плоскости одной из осей чертежа. На рис. 2.47 Σ║ П1 и Σ
Из проецирующего свойства вытекает, что плоскости уровня проецируются в линии, каждая на двух плоскостях проекций. На рис. 2.47 дано наглядное изображение горизонтальной плоскости уровня Σ. Характерной особенностью чертежей плоскостей уровня является параллельность главной (вырожденной) проекции плоскости одной из осей чертежа. На рис. 2.47 Σ║ П1 и Σ  П2, Σ
П2, Σ 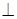 П3. Докажем, что Σ2║ х12.
П3. Докажем, что Σ2║ х12.
Известно, что если две параллельные плоскости пересечь третьей плоскостью, то образуются параллельные прямые. При пересечении П2 и П1 образуется ось х12. При пересечении П2 с Σ образуется ее главная проекция Σ2. Точно также доказывается, что Σ3║ у3.
Горизонтальная плоскость Г (а  b) представлена на рис. 2.48, а, фронтальная плоскость Т (а ║ b) - на рис. 2.48, б, профильная плоскость Ω (∆ АВС) - на рис. 2.48, в.
b) представлена на рис. 2.48, а, фронтальная плоскость Т (а ║ b) - на рис. 2.48, б, профильная плоскость Ω (∆ АВС) - на рис. 2.48, в.
2.4.7. Примеры на инцидентность. Рассмотрим несколько задач на взаимную принадлежность точки и прямой плоскости.
1) Через точку А провести плоскость общего положения Σ (а  b), где а ║ П1 и b ║ П2 (рис. 2.49, а).
b), где а ║ П1 и b ║ П2 (рис. 2.49, а).
Решение: через точку А(А1, А2) проводим проекции горизонтали а ║ П1 и фронтали b ║ П2. Возможны и другие варианты. Так, через точку А можно провести горизонталь или фронталь и пересечь ее прямой общего положения. Можно также через точку А провести две прямые общего положения. Однако в этом случае необходимо осуществить проверку на отсутствие в полученной плоскости профильно-проецирующих прямых, наличие которых указывает на получение профильно-проецирующей плоскости.
2) Заключить прямую а(а1, а2) общего положения в горизонтально- проецирующую плоскость Σ, задав ее своей главной проекцией Σ1 (рис. 2.49, б).
Решение: проводим главную проекцию Σ1 совпадающую с горизонтальной проекцией а1.
3) Построить горизонтальную проекцию прямой b общего положения, пересекающейся с прямой а, чтобы обе прямые принадлежали горизонтально-проецирующей плоскости Т (рис. 2.49, в).
Решение: проводим фронтальную проекцию прямой b так, чтобы b2 не была параллельна или перпендикулярна х12, а горизонтальная проекция b1 совпадала с а1. Главная проекция Т1 плоскости Т в этом случае совпадает с горизонтальными проекциями пересекающихся прямых а и b.
4) Пересечь прямую а прямой частного положения d так, чтобы обе прямые были заключены в горизонтально-проецирующую плоскость Г (рис. 2.49, г).
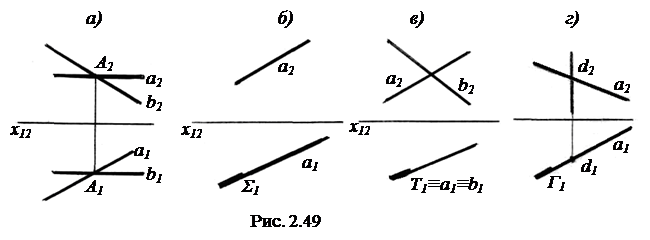 Решение: Прямую а в любом месте пересекаем горизонтально-проецирующей прямой d. Главная проекция Г1 горизонтально-проецирующей плоскости Г совпадает с горизонтальными проекциями а1 и d1 прямых.
Решение: Прямую а в любом месте пересекаем горизонтально-проецирующей прямой d. Главная проекция Г1 горизонтально-проецирующей плоскости Г совпадает с горизонтальными проекциями а1 и d1 прямых.
5) Заключить прямую а в профильно-проецирующую плоскость Ψ (рис. 2.50, а).
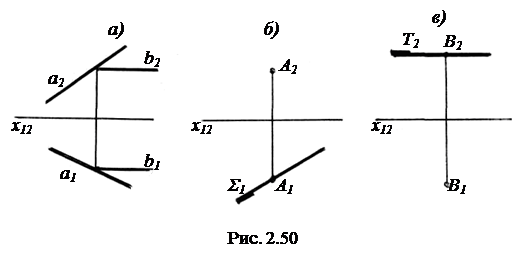
Решение: в простейшем случае пересекаем прямую а профильно- проецирующей прямой b 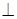 П3. Две пересекающиеся прямые а и b образуют профильно-проецирующую плоскость Ψ, т. к. если в плоскости имеется перпендикуляр к другой плоскости, то эти плоскости перпендикулярны между собой.
П3. Две пересекающиеся прямые а и b образуют профильно-проецирующую плоскость Ψ, т. к. если в плоскости имеется перпендикуляр к другой плоскости, то эти плоскости перпендикулярны между собой.
6) Через точку А провести горизонтально-проецирующую плоскость Σ (рис.2.50, б).
Решение: через точку А1 произвольно, но не перпендикулярно и не параллельно х12 проводим главную проекцию Σ1 плоскости Σ.
7) Через точку В провести горизонтальную плоскость уровня Т (рис. 2.50, в).
Решение: через точку В2 проводим главную проекцию Т2 плоскости Т параллельно х12.
2.4.8. Параллельность прямой и плоскости. Известно, что прямая параллельна плоскости, если она параллельна какой-либо прямой, расположенной в этой плоскости. Пусть, например, через точку М необходимо провести прямую d общего положения параллельно плоскости, заданной в виде треугольника - Σ (АВС) (рис. 2.51).
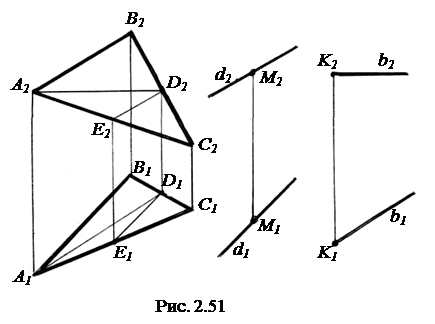 Решение: в плоскости Σ(АВС) проводим произвольную прямую общего положения ED(E1D1, E2D2). Далее через точку М1 проводим горизонтальную проекцию d1║ E1D1 и фронтальную проекцию d2║E2D2 прямой d.
Решение: в плоскости Σ(АВС) проводим произвольную прямую общего положения ED(E1D1, E2D2). Далее через точку М1 проводим горизонтальную проекцию d1║ E1D1 и фронтальную проекцию d2║E2D2 прямой d.
Если через точку К необходимо провести горизонталь b параллельно плоскости Σ (АВС), то построения следует выполнять в следующей последовательности:
1) Строим фронтальную проекцию A2D2 горизонтали AD параллельно оси х12.
2) В проекционной связи находим горизонтальную проекцию A1D1.
3) Через точки К1 и К2 проводим проекции b1║ A1D1 и b2 ║ A2D2 искомой горизонтали b. Следует отметить, что вовсе не обязательно горизонталь проводить через точку А, в чем рекомендуем читателю убедиться.
2.4.9. Параллельные плоскости.Для построения параллельных плоскостей используем признак их параллельности, известный из стереометрии: «Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым второй плоскости».
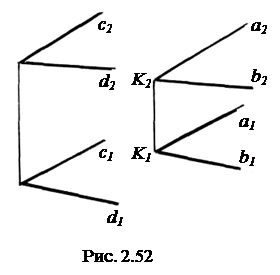 Пусть требуется через точку К (рис. 2.52) провести плоскость Σ (а
Пусть требуется через точку К (рис. 2.52) провести плоскость Σ (а  b) параллельно плоскости Т (с
b) параллельно плоскости Т (с  d). Для решения задачи через точку К проводим а ║ с так, чтобы а1║ с1 и а2║ с2, и b ║ d, чтобы b1 ║ d1 и b2 ║ d2.
d). Для решения задачи через точку К проводим а ║ с так, чтобы а1║ с1 и а2║ с2, и b ║ d, чтобы b1 ║ d1 и b2 ║ d2.
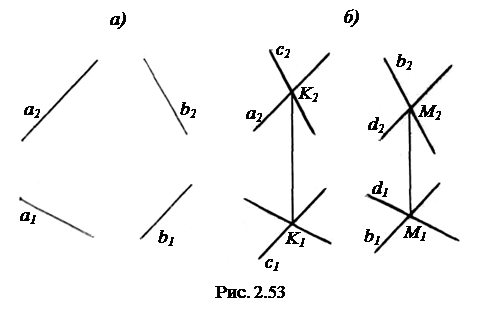 На рис. 2.53 рассмотрена задача, когда требуется прямые а и b заключить в пару параллельных плоскостей. Условие задачи дано на рис. 2.53, а. Для решения ее возьмем на прямых а и b произвольные точки К и М (рис. 2.53, б). Далее через точку К проводим прямую с ║ b, а через точку М прямую d ║ а. В результате получим параллельные плоскости Σ (а
На рис. 2.53 рассмотрена задача, когда требуется прямые а и b заключить в пару параллельных плоскостей. Условие задачи дано на рис. 2.53, а. Для решения ее возьмем на прямых а и b произвольные точки К и М (рис. 2.53, б). Далее через точку К проводим прямую с ║ b, а через точку М прямую d ║ а. В результате получим параллельные плоскости Σ (а  с) и Т (b
с) и Т (b  d), т. к. две пересекающиеся прямые а и с плоскости Σ соответственно параллельны двум пересекающимся прямым b и d плоскости Т.
d), т. к. две пересекающиеся прямые а и с плоскости Σ соответственно параллельны двум пересекающимся прямым b и d плоскости Т.
2.4.10. Построение проекций плоскости при замене плоскостей проекций.Для того, чтобы построить проекции плоскости при замене плоскости проекций, плоскость должна быть задана тремя точками. При построениях каждая точка, задающая плоскость, преобразуется подобно рассмотренному ранее при замене плоскостей проекций. На рис. 2.54 показано преобразование плоскости при произвольной замене плоскости проекций П2 на П4.
Самое сложное положение плоскости в пространстве – плоскость общего положения, более простое – проецирующая плоскость и самое простое - плоскость уровня. При решении задач плоскость обычно ставят из более сложного положения в более простое. Таким образом, ряд 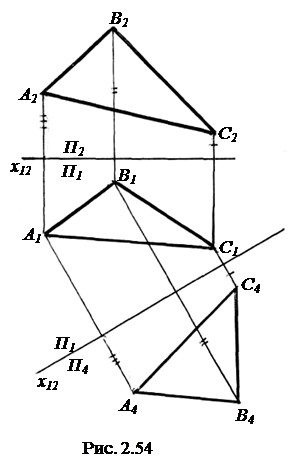 преобразований плоскости имеет вид: плоскость общего положения → плоскость проецирующая → плоскость уровня.
преобразований плоскости имеет вид: плоскость общего положения → плоскость проецирующая → плоскость уровня.
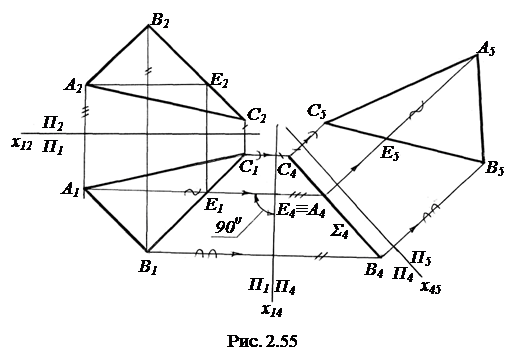
Сделаем первое преобра-зование. Пусть дана плоскость общего положения Σ(АВС) (рис. 2.55), и ее необходимо преобразовать во фронтально- проецирующую. В проецирующей плоскости всегда содержится проецирующая прямая. Любую прямую способом замены плоскостей проекций можно преобразовать в проецирующую: прямую общего положения - с помощью двух преобразований, прямую уровня – с помощью одного преобразования.
Для решения задачи выполним первое преобразование. Для этого:
1) В плоскости Σ(АВС) строим горизонталь АЕ (А2Е2, А1Е1).
2) Ставим АЕ в проецирующее положение, заменив П2 на П4 , причем х14 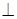 А1Е1.
А1Е1.
3) Проецируем треугольник на новую плоскость П4. При этом в системе П1–П4 треугольник АВС - проецирующий. Его новая фронтальная проекция А4В4С4 представляет собой прямую.
Выполним второе преобразование. В системе П1–П4 (рис. 2.53) Σ (ABC) - фронтально–проецирующая плоскость, и ее необходимо преобразовать в плоскость уровня. Любая плоскость уровня параллельна одной плоскости проекций и перпендикулярна двум другим. В данном случае Σ (АВС) 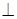 П4. Поэтому, если заменить П1 на П5, поставив П5 ║ Σ (АВС), то в системе П4–П5 плоскость Σ (АВС) станет плоскостью уровня.
П4. Поэтому, если заменить П1 на П5, поставив П5 ║ Σ (АВС), то в системе П4–П5 плоскость Σ (АВС) станет плоскостью уровня.
Произведем построения. Для этого:
1) Проведем ось х45 ║ Σ4.
2) В системе П4–П5 строим проекции точек А5, В5 и С5. Проекция треугольника А5В5С5 представляет его натуральную величину, т. к. плоскость Σ (АВС) ║ П5. При преобразовании плоскости общего положения в положение уровня выполнено два последовательных преобразования. Сначала заменена одна плоскость проекций, затем другая.
2.4.11. Классификация поверхностей.Произведем классификацию поверхностей по двум признакам:
По форме образующей:
1) Прямолинейную образующую имеют плоскости, многогранные поверхности и линейчатые кривые поверхности.
2) Криволинейную образующую, неизменяемую и изменяемую, - все остальные кривые поверхности.
По развертываемости поверхности на плоскость:
1) Развертываемые.
2) Неразвертываемые.
Развертыванием называется такая изометрическая деформация поверхности, при которой она может быть совмещена с плоскостью.
Изометрическую деформацию поверхности называют изгибанием. При изгибании отрезки линий, расположенных на поверхности, не меняют своей длины. Если поверхность может быть совмещена с плоскостью без складок и разрывов, то она развертываемая. Большинство поверхностей не совмещаемы с плоскостью без складок и разрывов и называются неразвертываемыми.
Развертываемыми являются многогранные поверхности и часть линейчатых – цилиндрические, конические и торсовые. О развертываемости плоскости говорить не приходится – она может быть совмещена с любой плоскостью.
Рассмотрим особенности построения изображений отдельных видов поверхностей.
2.4.12. Многогранные поверхности и многогранники. Принято считать ,что многогранной поверхностью называется поверхность, образованная частями (отсеками) пересекающихся плоскостей.
Поверхностью многогранного угла называется поверхность, ребра и грани которой пересекаются в одной точке (вершине). Если пересечь поверхность многогранного угла плоскостью, то образуется геометрическая фигура – пирамида.
Поверхность многогранного угла можно получить движением образующей прямой, которая все время проходит через вершину угла и в то же время скользит по направляющему многоугольнику.
Если вершину многогранного угла отнести в бесконечность, то ребра поверхности станут параллельными, и образуется призматическая поверхность.
Если ограничить призматическую поверхность двумя параллельными плоскими основаниями, то образуется геометрическая фигура – призма.
Определитель многогранной поверхности включает в себя направляющий многоугольник, вершину для многогранного угла и какое–либо ребро для призматической поверхности.
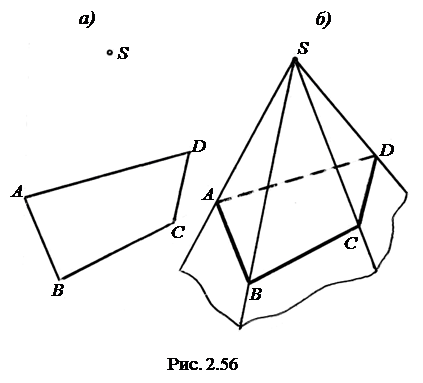
На рис. 2.56 показана поверхность многогранного угла Ф (ABCD, S) в пространственном изображении с направляющим четырехугольником ABCD и вершиной S. На рис. 2.56, а дан определитель поверхности. На рис. 2.56, б построен каркас поверхности.
 +
+
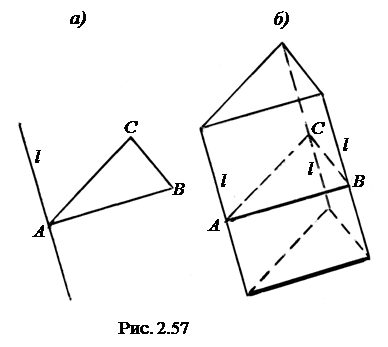
На рис. 2.57, а показана призматическая поверхность Ф (АВС, l) в пространственном изображении с направляющим треугольником АВС и образующей l; на рис. 2.57, б показана призма.
 Определителем пирамиды может быть ее основание и вершина. Определителем призмы – ее основание и одно боковое ребро или одна вершина другого основания.
Определителем пирамиды может быть ее основание и вершина. Определителем призмы – ее основание и одно боковое ребро или одна вершина другого основания.
При изображении многогранников их стараются расположить так, чтобы на проекциях их ребра и грани проецировались по возможности без искажения или с наименьшими искажениями.
Из всего многообразия многогранных поверхностей в качестве примера рассмотрим последовательность построения лишь правильных трёхгранных прямой призмы и пирамиды.
Прямая трехгранная правильная призма. На рис. 2.58, а дано графическое задание призмы Ф (АВС, 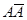 ) своим определителем. Для того, чтобы получить комплексный чертеж призмы (рис. 2.58, б), необходимо достроить два горизонтально–проецирующих ребра В
) своим определителем. Для того, чтобы получить комплексный чертеж призмы (рис. 2.58, б), необходимо достроить два горизонтально–проецирующих ребра В 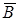 и С
и С 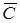 и три горизонтальных ребра верхнего основания
и три горизонтальных ребра верхнего основания 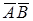 ,
, 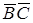 и
и 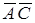 .
.
Проведем анализ элементов боковой поверхности призмы.
Боковые ребра – горизонтально–проецирующие прямые. Ребра оснований – горизонтали, из них ребра АС и 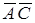 - профильно–проецирующие прямые.
- профильно–проецирующие прямые.
Боковые грани – горизонтально–проецирующие плоскости, из них грань 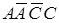 - фронтальная плоскость. Основания – горизонтальные плоскости. На горизонтальной проекции оба основания и их ребра проецируются в натуральную величину. На фронтальной проекции боковые ребра и задняя фронтальная грань
- фронтальная плоскость. Основания – горизонтальные плоскости. На горизонтальной проекции оба основания и их ребра проецируются в натуральную величину. На фронтальной проекции боковые ребра и задняя фронтальная грань 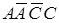 проецируются в натуральную величину.
проецируются в натуральную величину.
Рассмотрим примеры на инцидентность. Пусть дана проекция К2 точки К. Найти К1, считая, что точка лежит на видимой грани призмы (рис. 2.58, б).
На фронтальной проекции видны грани 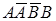 и
и 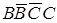 , грань
, грань 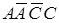 не видна. Поэтому считаем, что точка К лежит на видимой грани
не видна. Поэтому считаем, что точка К лежит на видимой грани 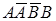 , и ее горизонтальная проекция К1 попадает на вырожденную проекцию грани (проецирующий след грани).
, и ее горизонтальная проекция К1 попадает на вырожденную проекцию грани (проецирующий след грани).
Пусть задана проекция М1 точки М. Найти М2, считая, что точка лежит на видимом основании призмы.
|
|
|
|
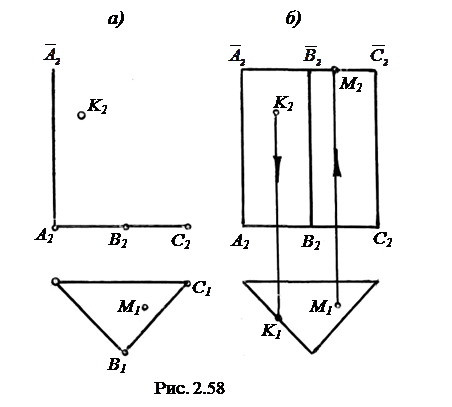
На горизонтальной проекции видно верхнее основание призмы 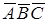 , а нижнее основание не видно. Поэтому фронтальная проекция М2 точки будет лежать на фронтальной проекции
, а нижнее основание не видно. Поэтому фронтальная проекция М2 точки будет лежать на фронтальной проекции 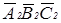 верхнего основания, слившегося в линию.
верхнего основания, слившегося в линию.
Правильная трехгранная пирамида.Определителем пирамиды Ф(АВС,S) служат её основание и вершина (рис. 2.59, а). Соединив вершину S с вершинами основания, получим полный каркас пирамиды. Комплексный чертеж пирамиды, заданный своим каркасом, приведен на рис. 2.59, б.
Проведем анализ элементов боковой поверхности пирамиды. В данной пирамиде все боковые ребра являются прямыми общего положения и проецируются в отрезки, меньшие их натуральных величин.
Боковые грани ASB и BSC являются плоскостями общего положения, а грань ASC – профильно-проецирующей плоскостью, так как она содержит профильно-проецирующее ребро АС.
Рассмотрим примеры на инцидентность. Пусть задана проекция К2 точки К. Найти К1 (рис. 2.59, б). Точка К лежит на видимой грани BSC. Горизонтальную проекцию находим, например, с помощью прямой общего положения, проходящей через точку К и вершину S (построения 1, 2, 3 и 4). Самостоятельно постройте проекцию К1 на рис. 2.59, а, где каркас пирамиды еще не построен.
Пусть задана проекция М2 точки М, построить М1. На фронтальной проекции видны грани ASB и BSC, а грань ASC не видна. Точка М должна лежать на видимой грани ASB.
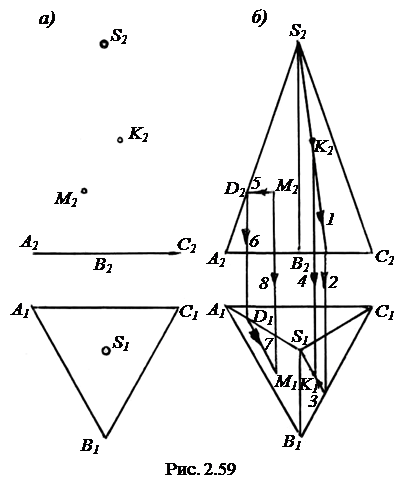 Проекцию М1 находим с помощью горизонтали, лежащей в плоскости грани ASB (построения 5, 6, 7 и 8). Фронтальная проекция горизонтали проведена через М2 параллельно оси х12 до пересечения с А2S2 в точке D2 (построение 5). С помощью линии связи на A1S1 находим точку D1 (построение 6). Проводим горизонтальную проекцию горизонтали параллельно ребру АВ, которое также является горизонталью. Известно, что все горизонтали одной плоскости параллельны (построение 7). Проекцию М1 с помощью линии связи находим на построенной проекции горизонтали (построение 8).
Проекцию М1 находим с помощью горизонтали, лежащей в плоскости грани ASB (построения 5, 6, 7 и 8). Фронтальная проекция горизонтали проведена через М2 параллельно оси х12 до пересечения с А2S2 в точке D2 (построение 5). С помощью линии связи на A1S1 находим точку D1 (построение 6). Проводим горизонтальную проекцию горизонтали параллельно ребру АВ, которое также является горизонталью. Известно, что все горизонтали одной плоскости параллельны (построение 7). Проекцию М1 с помощью линии связи находим на построенной проекции горизонтали (построение 8).
 2.4.13. Поверхности вращения. В соответствии с принятым в начертательной геометрии кинематическим способом образования поверхности, поверхность вращения образуется вращением прямолинейной или криволинейной образующей линии вокруг некоторой оси, как след движущейся линии.
2.4.13. Поверхности вращения. В соответствии с принятым в начертательной геометрии кинематическим способом образования поверхности, поверхность вращения образуется вращением прямолинейной или криволинейной образующей линии вокруг некоторой оси, как след движущейся линии.
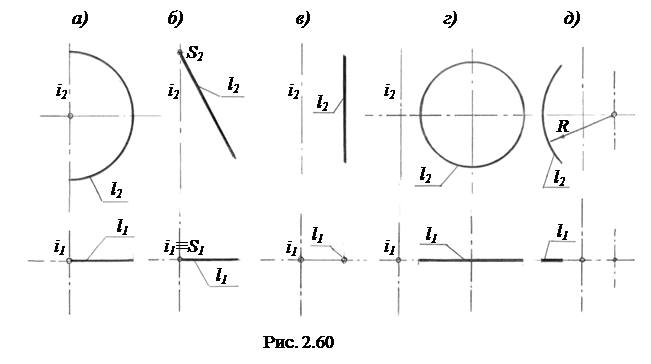
Поверхность вращения может быть задана определителем Ф (i, l), где i – ось вращения, l – образующая (рис.2.60). Тогда при вращения образующей l вокруг оси i получим следующие поверхности: сферическую (рис.2.60, а); коническую (рис.2.60, б); цилиндрическую (рис.2.60, в); торовую (открытую) (рис.2.60, г); торовую (закрытую) (рис.2.60, д).
При образовании поверхности вращения каждая точка образующей описывает окружность в плоскости, перпендикулярной оси вращения. При вращении точки вокруг оси имеем пять элементов процесса вращения (рис.2.61):
1) вращающаяся точка А;
2) ось вращения i;
3) плоскость вращения Т (проходит через точку А перпендикулярно оси вращения i);
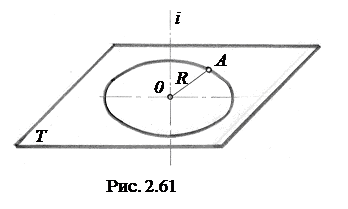 4) центр вращения О (точка пересечения плоскости Т с осью i);
4) центр вращения О (точка пересечения плоскости Т с осью i);
5) радиус вращения R=OA (отрезок, соедияющий центр О с точкой А).
 Вращаясь вокруг оси i, точка А описывает окружность, которая полностью лежит в плоскости вращения Т. Враща-ющаяся точка А и ось вращения i всегда известны, либо ими задаются.
Вращаясь вокруг оси i, точка А описывает окружность, которая полностью лежит в плоскости вращения Т. Враща-ющаяся точка А и ось вращения i всегда известны, либо ими задаются.
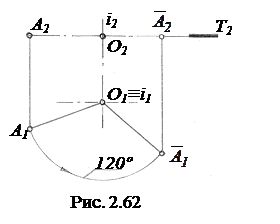
Пусть требуется повернуть точку А вокруг оси i на 1200 против часовой стрелки (рис. 2.62).
Из пяти элементов процесса вращения точка А и ось i (i ^ П1) заданы. Строим третий элемент – плоскость вращения Т. Плоскость вращения Т всегда перпендикулярна оси i, следовательно Т||П1 и Т^П2.
Плоскость Т – горизонтальная уровня, поэтому ее фронтальная проекция Т2, сливаясь в линию (проецирующий след плоскости), проходит через проекцию А2.
Находим четвертый элемент процесса вращения – центр вращения - точку О. Фронтальная проекция центра вращения О2 находится на пересечении i2 с Т2, а горизонтальная О1 совпадает с i1.
Пятый элемент процесса вращения – радиус R=OA. Так как фронтальная проекция О2А2||x12, то отрезок R=OA, являясь горизонталью, имеет горизонтальную проекцию О1А1, равную натуральной величине радиуса вращения (O1A1=R).
Окружность вращения расположена в плоскости Т и на П1 проецируется без искажения. Поэтому проводим окружность радиусом R=O1A1 с центром в точке О1. После поворота А1 по окружности на 1200 против часовой стрелки получаем горизонтальную проекцию точки А в новом положении 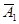 . Фронтальная проекция повернутой точки находится на пересечении линии связи, проводимой через
. Фронтальная проекция повернутой точки находится на пересечении линии связи, проводимой через 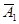 , и следа Т2 плоскости Т.
, и следа Т2 плоскости Т.
Элементы поверхностей вращения. Рассмотрим основные элементы поверхностей вращения, необходимые при построении проекций тел вращения. Введем понятие тела вращения.
Тело вращения – геометрическая объемная фигура, ограниченная поверхностью вращения. Помимо поверхности вращения тело вращения может иметь одно или два основания.
Плоскость, перпендикулярная оси вращения, пересекает поверхность вращения по окружности, которая называется параллелью (рис. 2.63). Окружности вращения точек, принадлежащих поверхности, являются параллелями. Самая большая параллель называется экватором, самая маленькая – горлом.
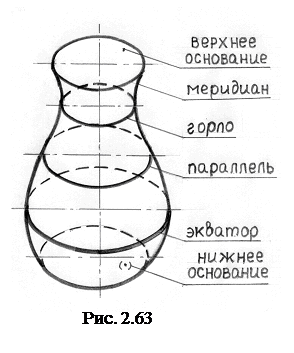 Плоскость, проходящая через ось вращения, называется меридианальной. Она пересекает поверхность по линии (кривой или прямой), которая называется меридианом. Можно сказать, что поверхность вращения образуется при вращении меридиана вокруг оси.
Плоскость, проходящая через ось вращения, называется меридианальной. Она пересекает поверхность по линии (кривой или прямой), которая называется меридианом. Можно сказать, что поверхность вращения образуется при вращении меридиана вокруг оси.
Рассмотрим построение проек-ций наиболее распространенных тел вращения (конуса, цилиндра, сферы, тора).
Конус вращения. Имеет определитель вида Ф(i, l), где i – ось вращения, l – образующая. Фронтальная проекция конуса вращения является его фронтальным очерком (рис. 2.64), который представляет из себя проекции S2A2 и S2C2 образующей в крайних левом и правом положениях относительно наблюдателя. При этом часть поверхности ABCS, обращенная к
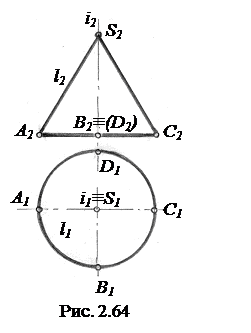 наблюдателю, видна, а часть поверхности ADCS не видна. Плоскость основания конуса параллельна П1. Поэтому фронтальная проекция основания есть прямая A2C2, параллельная оси х12 (ось х12 не показана).
наблюдателю, видна, а часть поверхности ADCS не видна. Плоскость основания конуса параллельна П1. Поэтому фронтальная проекция основания есть прямая A2C2, параллельная оси х12 (ось х12 не показана).
На горизонтальной проекции видна вся боковая поверхность конуса вращения.
Пусть требуется построить недостающие проекции точек М и К, расположенных на поверхности конуса вращения, определитель которого W (l, i) (рис.2.65, а); требуется также построить фронтальный и горизонтальный очерки конуса.
Для решения задачи через М2 проводим главную проекцию 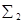 плоскости вращения
плоскости вращения 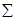 так, что
так, что 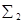 ^ i2 (рис.2.65, б). Строим О2=
^ i2 (рис.2.65, б). Строим О2= 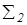 Ç i2 и N2=
Ç i2 и N2= 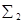 Çl2. По линии проекционной связи находим О1 º i1 и N1Îl1. Очевидно, радиус вращения R точки N равен О1N1. Радиусом вращения R=O1N1 с центром в точке О1 строим горизонтальную проекцию окружности вращения точки N. Фронтальная проекция окружности вращения проецируется в виде отрезка
Çl2. По линии проекционной связи находим О1 º i1 и N1Îl1. Очевидно, радиус вращения R точки N равен О1N1. Радиусом вращения R=O1N1 с центром в точке О1 строим горизонтальную проекцию окружности вращения точки N. Фронтальная проекция окружности вращения проецируется в виде отрезка 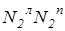 , совпадающего с
, совпадающего с 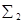 , где
, где 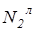 и
и 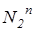 - соответственно фронтальные проекции точки N в крайнем левом и крайнем правом положениях относительно наблюдателя.
- соответственно фронтальные проекции точки N в крайнем левом и крайнем правом положениях относительно наблюдателя.
Фронтальные очерковые образующие конуса проходят через точки 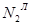 , S2 и
, S2 и 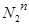 , S2.
, S2.
Для нахождения М1 через М2 проводим линию проекционной связи до пересечения с построенной окружностью. Далее находим К2. Для этого через К1 проводим параллель радиусом R=O1K1, отмечаем крайнее правое (можно крайнее левое) положение 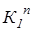 и по линии проекционной связи в точке пересечения с фронтальной очерковой образующей, проходящей через точки S2 и
и по линии проекционной связи в точке пересечения с фронтальной очерковой образующей, проходящей через точки S2 и 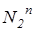 , находим
, находим 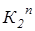 . Проекция
. Проекция 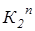 расположена на главной проекции Т2 плоскости вращения точки К. На фронтальной проекции окружности вращения
расположена на главной проекции Т2 плоскости вращения точки К. На фронтальной проекции окружности вращения 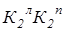 по линии проекционной связи находим К2. Проекция К2 не видна.
по линии проекционной связи находим К2. Проекция К2 не видна.
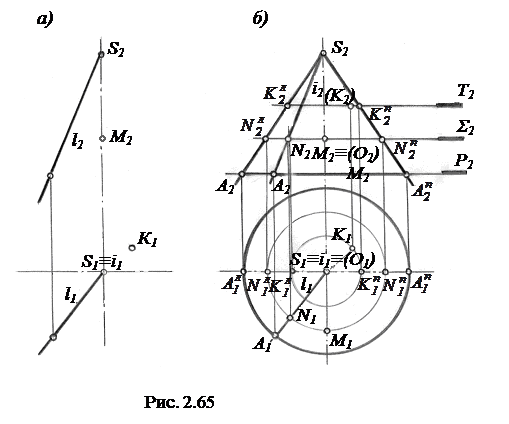
Очерк поверхности конуса содержит не только проекции очерковых образующих, но и проекции основания. Поэтому, обозначая некоторую точку А на образующей l и используя рассмотренный прием введения плоскости вращения Р точки А, имеем фронтальный очерк конуса в виде треугольника 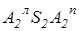 и горизонтальный очерк в виде окружности радиуса R=O1A1.
и горизонтальный очерк в виде окружности радиуса R=O1A1.

Линию на поверхности строят по точкам, задаваясь крайними точками на границе видимости (при наличии таковых), ближайшими к оси вращения и промежуточными. Следует иметь в виду, что очерковые образующие являются границей видимости. Общее количество выбранных на кривой линии точек должно быть не менее 4-6. Аналогичный подход сохраняется и для других поверхностей вращения, рассматриваемых ниже.
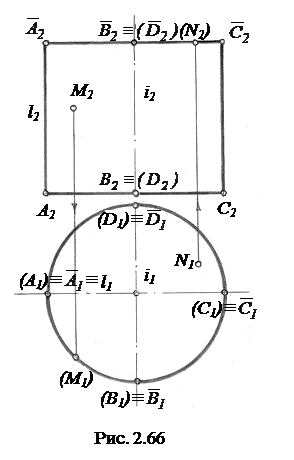
Цилиндр вращения. Имеет определитель Ф(l, i), где l – образующая прямая линия, i – ось вращения. Боковая поверхность такого цилиндра горизонтально–проецирующая, т.к. все его образующие перпендикулярны П1 и, перемещаясь в пространстве, пересекают все точки окружности основания (рис.2.66).
Проекции образующих 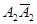 и
и 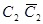 вместе с проекциями верхнего
вместе с проекциями верхнего 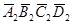 и нижнего A2B2C2D2 оснований являются фронтальным очерком цилиндра. На фронтальной проекции видна часть поверхности
и нижнего A2B2C2D2 оснований являются фронтальным очерком цилиндра. На фронтальной проекции видна часть поверхности 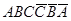 и не видна
и не видна 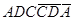 . На горизонтальной проекции боковая поверхность цилиндра проецируется в окружность. Верхнее основание
. На горизонтальной проекции боковая поверхность цилиндра проецируется в окружность. Верхнее основание 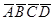 видно на горизонтальной проекции, нижнее ABCD не видно. Построение проекций точек М и N и их видимость показаны на рис.2.66.
видно на горизонтальной проекции, нижнее ABCD не видно. Построение проекций точек М и N и их видимость показаны на рис.2.66.
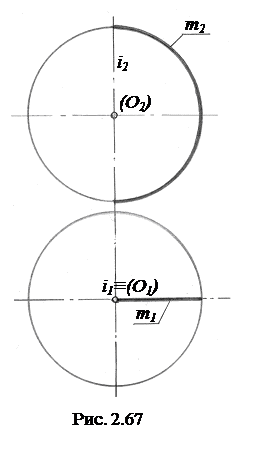
 Сфера. Имея определитель вида Ф(m, i), поверхность сферы образуется вращением полуокружности (меридиана) m вокруг оси i, проходящей через её центр и лежащей в плоскости этой полуокружности (рис. 2.67).
Сфера. Имея определитель вида Ф(m, i), поверхность сферы образуется вращением полуокружности (меридиана) m вокруг оси i, проходящей через её центр и лежащей в плоскости этой полуокружности (рис. 2.67).
|
|
Две другие проекции экватора проецируются в отрезки прямых
 Э2 || х12 и Э3 || у3. При рассечении сферы фронтальной плоскостью уровня S, проходящей через центр сферы О и ее ось i, поверхность рассекается по окружности N. Горизонтальная проекция N1 этой окружности есть отрезок прямой, равный диаметру сферы. Фронтальная проекция N2 есть натуральная величина окружности и является фронтальным очерком сферы. Профильная проекция N3 также представляет из себя отрезок прямой, равный диаметру сферы.
Э2 || х12 и Э3 || у3. При рассечении сферы фронтальной плоскостью уровня S, проходящей через центр сферы О и ее ось i, поверхность рассекается по окружности N. Горизонтальная проекция N1 этой окружности есть отрезок прямой, равный диаметру сферы. Фронтальная проекция N2 есть натуральная величина окружности и является фронтальным очерком сферы. Профильная проекция N3 также представляет из себя отрезок прямой, равный диаметру сферы.
Если рассечь сферу профильной плоскостью уровня Т, проходящей через центр О и ось i, то поверхность сферы также рассечется по окружности L. Фронтальная L2 и горизонтальная L1 проекции ее являются отрезками прямых, равными диаметру сферы. Профильная проекция L3 есть натуральная величина окружности и является профильным очерком сферы.
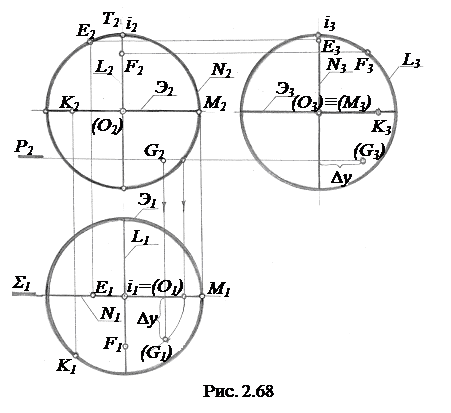
На рис. 2.68 показаны проекции точек К, Е и F, расположенных на соответствующих очерковых окружностях Э, N и L. Все проекции точек видимые, поскольку на горизонтальной проекции видно верхнее полушарие,
ограниченное экватором Э (нижнее не видно), на фронтальной проекции видно переднее полушарие, ограниченное проекцией окружности N фронтального очерка (задняя часть не видна) и на профильной проекции видно левое полушарие, ограниченное проекцией окружности L профильного очерка.
Для нахождения проекций G1 и G3 точки G, заданной на сфере проекцией G2, через точку G проводим горизонтальную уровня плоскость Р, которая рассекает сферу по параллели. На горизонтальной проекции радиусом этой параллели в зоне расположения точки G проводим дугу окружности и на пересечении её с линией проекционной связи, проведенной из точки G2, находим G1. Проекция G3 расположена на линии проекционной связи, проведенной из точки G2, на расстоянии Dу от i3. Проекции G1 и G3 не видны.
Если задана G1 и необходимо найти G2 и G3, то построения проводят в обратном порядке.
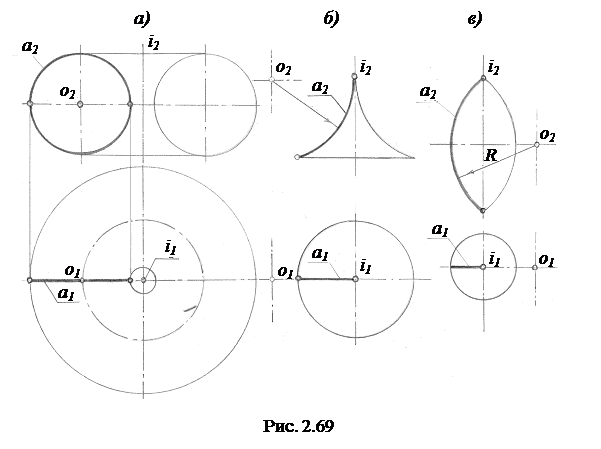
Тор. Имеет определитель вида Ф (а, i), где а – окружность или часть ее, i – ось вращения. Поверхность тора образуется вращением окружности а или части ее вокруг оси i, лежащей в плоскости окружности или ее дуги и не проходящей через центр О (рис. 2.69).
В зависимости от расположения оси i относительно образующей а имеем различные разновидности поверхностей торов. Если ось i лежит вне окружности (рис. 2.69, а), то образуется открытая торовая поверхность, похожая на поверхность баранки. Если ось i пересекается с дугой окружности или её продолжением, то может получится вогнутая (рис. 2.69, б) или выпуклая (рис. 2.69, в) закрытая торовая поверхность.
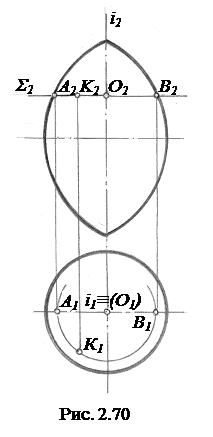
Пусть требуется найти горизонтальную проекцию К1 точки К, расположенной на поверхности тора, заданного фронтальным и горизонтальным очерками (рис. 2.70). Тогда через точку К проводим плоскость вращения  ^i, которая рассекает поверхности по окружности, фронтальная проекция которой есть отрезок прямой А2В2. Радиусом R=О2А2=О2В2 строим горизонтальную проекцию параллели – окружность, на пересечении с которой линии проекционной связи, проведенной из точки К2, находим проекцию К1. Проекция К1 видимая, т.к. лежит на верхней половине тора выше экватора.
^i, которая рассекает поверхности по окружности, фронтальная проекция которой есть отрезок прямой А2В2. Радиусом R=О2А2=О2В2 строим горизонтальную проекцию параллели – окружность, на пересечении с которой линии проекционной связи, проведенной из точки К2, находим проекцию К1. Проекция К1 видимая, т.к. лежит на верхней половине тора выше экватора.
Если задана проекция К1, и надо найти проекцию К2 , то построение выполняем в обратном порядке.
| <== предыдущая страница | | | следующая страница ==> |
| Проекции кривых линий | | | ПОЗИЦИОННЫЕ ЗАДАЧИ |
Дата добавления: 2014-09-26; просмотров: 2274; Нарушение авторских прав

Мы поможем в написании ваших работ!