МЕТОДИКА ЭКСПЕРИМЕНТА

Чтобы результаты эксперимента могли быть распространены на все подобные явления, их необходимо обработать в безразмерной форме. Уравнение подобия для вынужденной конвекции воздуха в трубе имеет вид:

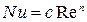, (4.6)

где с и n – константы, которые определяются из опыта; 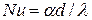– число Нуссельта, определяющее соотношение теплопроводности 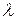, Вт/(м×К) внутри пограничного слоя жидкости и конвективной теплоотдачи 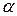, Вт/(м²×К) на его границе; 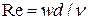– число Рейнольдса, характеризующее режим вынужденного движения жидкости; w – средняя скорость воздуха в трубе, м/с; 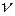- кинематическая вязкость воздуха, м²/с.

Если зависимость (4.6) прологарифмировать, то в логарифмических координатах она будет представлять уравнение прямой линии (см. рис. 4.2):

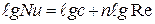. (4.7)

Логарифм константы с отсекается в начале координат прямой АС, а показатель степени n находится из прямоугольного треугольника АВС, с учетом масштабов по осям координат:

.

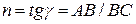Методика обработки экспериментальных данных:

• по опытным данным определяются коэффициенты теплоотдачи a ;

• рассчитываются числа подобия Нуссельта (теплопроводность воздуха 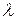брать из рис. 4.4);

• находятся числа подобия Рейнольдса (коэффициенты кинематической вязкости воздуха 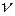взять по рис. 4.4);

• по результатам расчета строится в логарифмических координатах прямолинейная зависимость (см. рис. 4.2);

• из графика находятся константы с и n;

• с учетом найденных значений констант записывается уравнение подобия 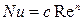, которое справедливо для подобных явлений теплоотдачи при вынужденном движении воздуха внутри труб.

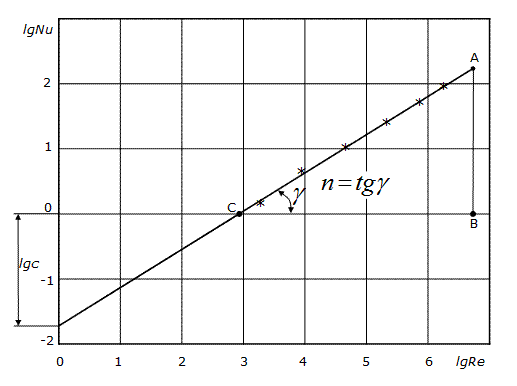
Рис. 4.2. Графическое обобщение экспериментальных данных

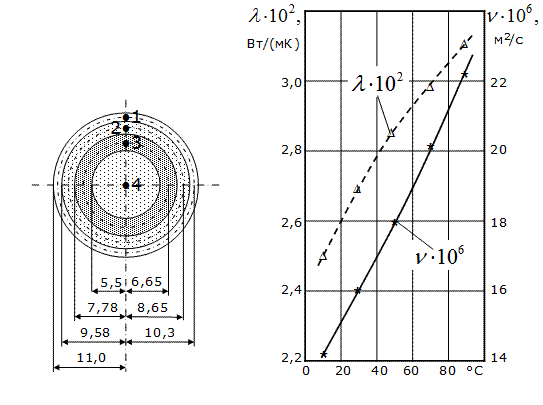
Рис. 4. 3. Точки 1…4 измерений динамических напоров 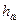в равновеликих сечениях

Рис. 4.4. Физические свойства воздуха

Дата добавления: 2014-09-29; просмотров: 193; Нарушение авторских прав

Мы поможем в написании ваших работ!