
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Проектирование элементов корпуса из тяжелого бетона без предварительного напряжения
7.1 Экспериментальные основы теории сопротивления железобетона
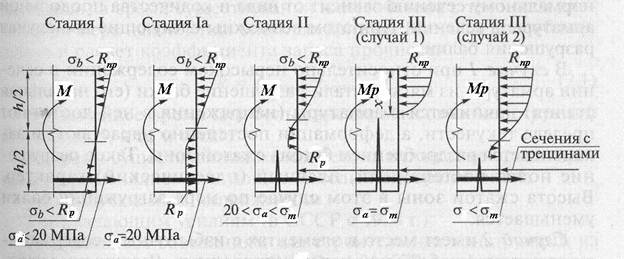
Общая теория прочности железобетона исходит из напряженно-деформированного состояния элемента на различных стадиях его нагружения. Опытами установлено, что при изгибе железобетонных балок нагрузкой вплоть до их разрушения, когда изгибающий момент М равен разрушающему изгибающему моменту Мр, в нормальных сечениях балки наблюдаются три характерные стадии напряженно-деформированного состояния (рис. 7.1).
|
| Рис. 7.1 – Стадии напряженно-деформированного состояния при изгибе: Мр – расчетный разрушающий момент |
Стадия I имеет место при небольших нагрузках (М ≤ Мр ) до образования трещин в растянутой зоне бетона. Напряжения в бетоне и арматуре невелики, деформации носят в основном упругий характер, а эпюры напряжений имеют форму треугольников. В конце стадии (стадия Ia) в волокнах бетона растянутой зоны развиваются неупругие деформации при напряжениях в бетоне, равных расчетному сопротивлению бетона растяжению Rp, а напряжения в растянутой продольной арматуре равны 20 МПа. По стадии Ia рассчитывают изгибаемые элементы на образование трещин и деформации.
При росте нагрузки (0,2M < M < 0,6M) бетон растянутой зоны сечения разрушается и в сечении по трещине не работает (стадия II). В сечении по трещине все внутренние растягивающие усилия воспринимает стальная арматура. На участках между трещинами сцепление арматуры с бетоном не нарушено. Бетон работает на растяжение, а напряжения растяжения в арматуре уменьшаются. С ростом нагрузки трещины в бетоне растянутой зоны раскрываются, а напряжения в растянутой арматуре в отдельных случаях могут достигнуть предела текучести σт. В сжатой зоне бетона развиваются неупругие деформации, как следствие, эпюра нормальных напряжений искривляется. Напряжения в бетоне сжатой зоны меньше призменной прочности бетона. В стадии II изгибающий момент может достигнуть 65% от разрушающего момента 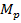 . По стадии II рассчитывают величину раскрытия нормальных трещин и кривизну элемента.
. По стадии II рассчитывают величину раскрытия нормальных трещин и кривизну элемента.
Стадия III (стадия разрушения) характеризуется коротким периодом работы балки. Криволинейность эпюры напряжений сжатия в бетоне становится ярко выраженной и приближается по очертанию к кубической параболе. Бетон растянутой зоны из работы почти полностью исключается. Характер разрушения сечения зависит от вида и количества продольной рабочей арматуры. При этом возможны два следующих случая разрушения балки:
В случае 1 при относительно невысоком содержании в сечении арматуры из мягкой стали разрушение балки начинается с растянутой арматуры, напряжения в которой достигают предела текучести. Деформация балки растет, уменьшается высота сжатой зоны бетона 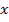 . Как следствие, напряжения в бетоне сжатой зоны растут и достигают предела - призменной прочности бетона
. Как следствие, напряжения в бетоне сжатой зоны растут и достигают предела - призменной прочности бетона 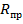 . В сечении образуется пластический шарнир с предельными значениями напряжений в бетоне и арматуре. Относительно пластического шарнира происходит поворот частей балки и плавное разрушение.
. В сечении образуется пластический шарнир с предельными значениями напряжений в бетоне и арматуре. Относительно пластического шарнира происходит поворот частей балки и плавное разрушение.
Случай 2 имеет место в элементах с избыточным содержанием арматуры или переармированных. Разрушение переармированного элемента происходит хрупко по бетону сжатой зоны при напряжениях в бетоне, равных призменной прочности. Напряжения в растянутой арматуре при разрушении не достигают предела текучести. Переход из стадии II в стадию III происходит внезапно. Применение таких элементов нежелательно, так как они неэкономичны. По III стадии напряженно – деформированного состояния выполняют расчет прочности нормальных сечений, где эпюра нормальных напряжений в бетоне принимается прямоугольной с ординатой 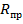 .
.
Во время работы изгибаемого элемента его сечения по длине испытывают разные стадии напряженно – деформированного состояния.
Аналогичные стадии напряженно-деформированного состояния имеют место при внецентренном сжатии и внецентренном растяжении, когда эпюры нормальных напряжений имеют два знака.
При изгибе железобетонной балки действуют одновременно нормальные σ и касательные напряжения τ, которые формируют главные напряжения в наклонных сечениях. Главные напряжения в наклонных сечениях равны
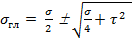 (1)
(1)
Главные сжимающие напряжения воспринимает бетон, они опасности не представляют. Как только главные растягивающие напряжения превышают предел прочности бетона осевому растяжению 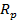 , в наклонном сечении появляется трещина. В сечении по наклонной трещине поперечная сила воспринимается бетоном сжатой зоны и поперечной арматурой, пересекающей наклонное сечение. Разрушение балки по наклонному сечению вызывается одной из следующих причин:
, в наклонном сечении появляется трещина. В сечении по наклонной трещине поперечная сила воспринимается бетоном сжатой зоны и поперечной арматурой, пересекающей наклонное сечение. Разрушение балки по наклонному сечению вызывается одной из следующих причин:
1. Преодолевается сопротивление арматуры и происходит поворот обеих частей балки вокруг общего шарнира, расположенного в сжатой зоне бетона. Арматура течет, или при слабой анкеровке выдергивается из бетона. Высота сжатой зоны уменьшается и бетон разрушается.
2. При достаточном количестве и хорошей анкеровке продольной арматуры происходит смещение одной части балки относительно другой под действием поперечной силы. Разрушается поперечная арматура и бетон сжатой зоны сечения.
3. Таким образом, должны быть обеспечены два условия прочности балки по наклонному сечению: по изгибающему моменту и по поперечной силе.
7.2 Методы расчета прочности сечений железобетонных элементов
7.2.1 Метод расчета по допускаемым напряжениям сложился в общих чертах в конце 19 века. За основу принята вторая стадия напряженно деформированного состояния сечения элемента при допущении следующих гипотез: а) бетон растянутой зоны сечения не работает; б) бетон сжатой зоны сечения и растянутая продольная арматура работают упруго; в) связь между напряжениями и деформациями линейная в соответствии с законом Гука); г) справедлива гипотеза плоских сечений( т.е. нормальные к продольной оси сечения, плоские до изгиба, остаются плоскими после изгиба); д) постоянным является отношение модуля упругости арматуры 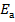 к начальному модулю упругости бетона
к начальному модулю упругости бетона 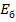
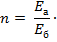
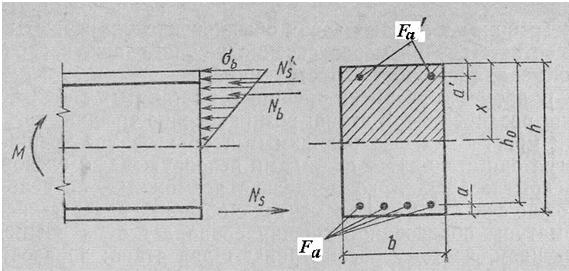
Расчетная схема сечения по допускаемым напряжениям приведена на рис. 7.2, где рассматривается приведенное к бетону однородное сечение с начальным модулем упругости 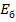 . Площадь сечения растянутой арматуры
. Площадь сечения растянутой арматуры 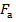 и площадь сечения сжатой арматуры
и площадь сечения сжатой арматуры 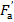 заменяются площадью бетона:
заменяются площадью бетона: 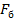 =
= 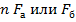 =
= 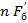 .
.
|
Рис. 7.2 – Расчетная схема нормального сечения по допускаемым напряжениям: М – расчетный изгибающий момент;x – высота сжатой зоны бетона; 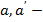 расстояние от центра тяжести арматуры площадью расстояние от центра тяжести арматуры площадью 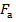 , , 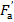 до наиболее удаленного волокна бетона; до наиболее удаленного волокна бетона; 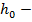 рабочая высота сечения, рабочая высота сечения, 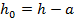 ; ; 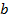 – ширина сечения – ширина сечения
|
Из равенства относительных деформаций бетона и арматуры 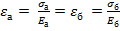
определим нормальное напряжение в арматуре 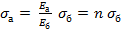 .
.
Максимальное нормальное напряжение в сжатом бетоне для приведенного сечения определяется по формуле
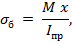
где 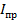 - момент инерции приведенного сечения относительно нейтральной оси
- момент инерции приведенного сечения относительно нейтральной оси
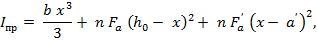
x – высота сжатой зоны бетона, определяемая из равенства нулю статического момента приведенной площади сечения 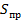 относительно нейтральной оси
относительно нейтральной оси
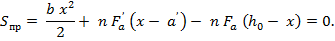
Максимальное нормальное напряжение в растянутой продольной арматуре определяется по формуле
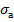 =
= 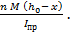
Условия прочности сечения по допускаемым напряжениям имеют следующий вид:
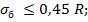
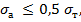
где R – марка бетона. равная кубиковой прочности бетона;
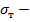 предел текучести арматуры.
предел текучести арматуры.
Недостатки метода:
• действительное распределение напряжений в сжатой зоне бетона на стадии 11 не соответствует треугольной эпюре вследствие развития деформаций ползучести бетона;
• число n – величина переменная;
• допускаемые напряжения являются условными величинами и не позволяют судить о действительном запасе прочности элементов конструкции.
Конструкции судов и доков, спроектированные с использованием данного метода расчета явились достаточно надежными, но данный метод приводил к некоторому перерасходу материалов.
7.2.2 Метод расчета сечений по разрушающим усилиям (1938 г) основан на стадии III напряженно – деформированного состояния изгибаемых элементов (стадии разрушения). Работа бетона растянутой зоны не учитывается. В расчетные формулы вместо допускаемых напряжений вводят предел прочности бетона при сжатии и предел текучести арматуры. Значение модуля упругости бетона не требуется. Эпюра напряжений в бетоне сжатой зоны принимается прямоугольной. Усилие, допускаемое при эксплуатации конструкции, определят делением разрушающего усилия на общий коэффициент запаса прочности 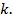
Коэффициент запаса прочности 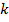 был установлен нормами в зависимости от причины разрушения конструкции , сочетания силовых воздействий и отношения усилий
был установлен нормами в зависимости от причины разрушения конструкции , сочетания силовых воздействий и отношения усилий 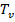 от временных нагрузок к усилиям
от временных нагрузок к усилиям 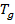 от постоянных нагрузок. Например, для плит и балок при основном сочетании нагрузок и отношении
от постоянных нагрузок. Например, для плит и балок при основном сочетании нагрузок и отношении 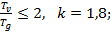 при
при 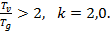
Изгибающий момент, допускаемый при эксплуатации судна, определяется по формуле
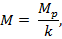
где 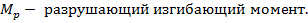
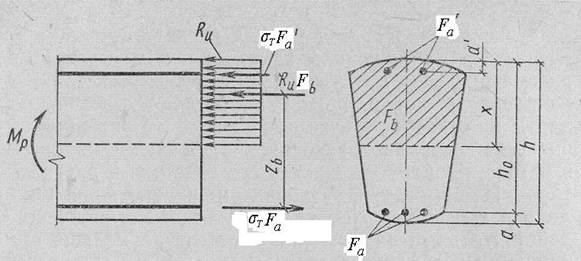
При определении разрушающих усилий сечений элементов, разрушающихся по случаю 1, разрушение которых начинается в растянутой зоне, применяют принцип пластического шарнира. В пластическом шарнире с односторонним трением напряжения в арматуре и бетоне сечения достигают предельных значений одновременно. Расчетная схема для изгибаемого элемента любой симметричной формы сечения приведена на рис. 7.3
Осевая сжимающая сила, допускаемая при эксплуатации сжатых элементов, определяется по формуле
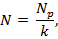
где 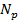 - разрушающая осевая сила.
- разрушающая осевая сила.
|
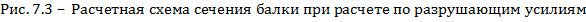
|
Высоту сжатой зоны бетона x для изгибаемых элементов определяют из условия равновесия внутренних усилий в стадии разрушения
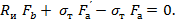
где 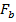 - площадь сжатой зоны бетона, для прямоугольного сечения
- площадь сжатой зоны бетона, для прямоугольного сечения 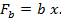
Разрушающий изгибающий момент определяют как момент внутренних усилий относительно оси, проходящей через центр тяжести растянутой арматуры
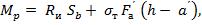
где 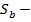 статический момент площади сечения бетона сжатой зоны относительно оси, проходящей через центр тяжести растянутой арматуры,
статический момент площади сечения бетона сжатой зоны относительно оси, проходящей через центр тяжести растянутой арматуры, 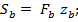
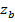 - расстояние от центра тяжести сечения растянутой арматуры до центра тяжести площади сечения сжатой зоны бетона.
- расстояние от центра тяжести сечения растянутой арматуры до центра тяжести площади сечения сжатой зоны бетона.
Граница между первым и вторым случаями разрушения устанавливается на основе опытных данных. При 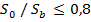 разрушение сечения происходит по случаю I
разрушение сечения происходит по случаю I
( 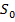 – статический момент всей рабочей площади сечения бетона относительно оси, проходящей через центр тяжести сечения растянутой арматуры). Для прямоугольных и тавровых сечений с полкой в сжатой зоне граничное значение высоты сжатой зоны бетона
– статический момент всей рабочей площади сечения бетона относительно оси, проходящей через центр тяжести сечения растянутой арматуры). Для прямоугольных и тавровых сечений с полкой в сжатой зоне граничное значение высоты сжатой зоны бетона 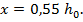
В расчетах сечений по разрушающим усилиям внутренние усилия M, Q, N от нагрузки также определяются с учетом образования пластических шарниров, что позволяет сократить расход материалов.
Преимущество метода: он позволяет установить для конструкции общий коэффициент запаса прочности.
Недостаток: не отражает работу конструкции в стадии эксплуатации. В связи с этим проверку жесткости и трещиностойкости по II стадии напряженно – деформированного состояния сечений железобетонных элементов.
Расчет по разрушающим усилиям сохранился в качестве основного метода в Правилах Российского Речного Регистра с некоторыми уточнениями, полученными на основе опыта эксплуатации и результатов научно – экспериментальных работ.
7.2.3 Метод предельных состояний (1955 г). Предельным называется такое состояние конструкции, при котором ее дальнейшая эксплуатация становится невозможной. При наступлении предельных состояний первой группы (нарушение прочности, устойчивости, выносливости) конструкция превращается в механизм, который эксплуатировать невозможно. Предельное состояние первой группы не наступает, если максимальное усилие в элементе при наиболее неблагоприятном сочетании нагрузок и воздействий не превышает минимальной несущей способности элемента. Расчет прочности выполняется по III стадии напряженно – деформированного состояния сечения.
При наступлении предельных состояний второй группы (по деформациям, по образованию и раскрытию трещин) нормальная эксплуатация конструкции невозможна, требуется ее ремонт. Предельное состояние второй группы не наступает, если деформации, ширина раскрытия трещин не превышают предельно допустимых значений, установленных нормами проектирования. Расчет предельных состояний второй группы выполняется по I или II стадиям напряженно - деформированного состояния сечений.
В железобетонном судостроении метод не применяется ввиду отсутствия необходимого статистического материала.
7.3 Расчет судовых конструкций из обычного железобетона
7.3.1 Определение внешних нагрузок.По своей природе нагрузки, действующие на судно, подразделяются на две категории:
• вызываемые воздействием окружающей среды (волнения, ветра, течения, льда, сейсмические, температурные);
• создаваемые весом судна, а также работой механизмов, устройств, систем и другие, связанные с функционированием судна.
Каждая из категорий может включать постоянные и переменные во времени нагрузки. По характеру реакции конструкции на внешнее воздействие переменные нагрузки делятся на статические и динамические. По относительным размерам зоны своего влияния каждая из указанных категорий нагрузок подразделяется на глобальные (общие) и локальные (местные).
Постоянные статические нагрузки – это нагрузки, не изменяющиеся по величине, положению и направлению при изменении внешних условий (вес судна, вес всего постоянно закрепленного оборудования, силы поддержания при положении судна на тихой воде.
Переменными (случайными) статическими нагрузками являются нагрузки, изменяющиеся во времени по величине и направлению ( ветровая, волновая, ледовая, от веса груза, при навале на сооружение, при испытании корпуса на водонепроницаемость, нагрузки при постановке судна в док). Скорость изменения этих нагрузок настолько мала, что они не оказывают динамического эффекта на конструкцию.
Аварийнымиявляются нагрузки, которые могут привести часть конструкций корпуса в состояние, требующее их замены или ремонта, но не вызывающее разрушения корпуса в целом. К ним относятся глобальные нагрузки при затоплении отсека, при посадке на мель или навале на стенку, гидростатические нагрузки на переборки при затоплении отсека .
Динамическими являются нагрузки, изменяющиеся по величине, положению и направлению достаточно быстро (время изменения близко к периоду собственных колебаний конструкции корпуса судна), чтобы вызвать динамический эффект в поведении конструкции. Динамический эффект в конструкции способны создать порывы ветра, волнение, ледовая и сейсмическая нагрузки.
Прочность корпуса судна должна быть проверена на наихудшее сочетание внешних нагрузок, при котором возможно возникновение наибольших напряжений в конструкции.
Расчетные нагрузки при общем изгибе корпуса судна.При общем изгибе корпус судна рассматривается как балка (зквивалентный брус), в которую включаются все находящиеся в рассматриваемом сечении продольные непрерывные связи корпуса, протяженность которых превышает удвоенную высоту борта, при условии, что соединение этих связей с корпусом обеспечивает их участие в общем изгибе судна. В приведенную площадь эквивалентного бруса включают всю площадь поперечного сечения арматуры и 1/10 площади поперечного сечения сжатой зоны бетона.
Для вычисления изгибающих моментов 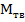 и срезывающих сил
и срезывающих сил 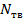 на тихой воде необходимо интегрировать кривую нагрузки не менее, чем по 21 равноотстоящей ординате при наиболее неблагоприятных сочетаниях нагрузки, например,
на тихой воде необходимо интегрировать кривую нагрузки не менее, чем по 21 равноотстоящей ординате при наиболее неблагоприятных сочетаниях нагрузки, например,
• судно порожнем с балластом, с 10% и 100% запасов и топлива;
• судно в полном грузу;
• судно при аварийном затоплении отсеков;
• другие неблагоприятные случаи нагрузки (перевозка тяжеловесов, неполное использование грузоподъемности и т.п.).
Изгибающие моменты 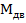 и срезывающие силы
и срезывающие силы 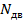 на волне определяют путем постановки судна на вершину или подошву регулярной волны, высота которой определяется классом судна. Методика расчета приведена в Правилах РРР и учитывает статическое и динамическое воздействие волны на корпус судна. Максимальное значение дополнительной волновой перерезывающей силы определяется по формуле
на волне определяют путем постановки судна на вершину или подошву регулярной волны, высота которой определяется классом судна. Методика расчета приведена в Правилах РРР и учитывает статическое и динамическое воздействие волны на корпус судна. Максимальное значение дополнительной волновой перерезывающей силы определяется по формуле
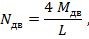
где L – длина судна по конструктивной ватерлинии.
Расчетное значение изгибающих моментов для прогиба и перегиба вычисляется
суммированием значений изгибающего момента на тихой воде с дополнительным волновым изгибающим моментом, аналогично для перерезывающей силы:
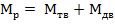 ;
;
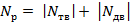 ,
,
где 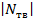 - абсолютное значение перерезывающей силы на тихой воде.
- абсолютное значение перерезывающей силы на тихой воде.
Продольные силы в элементах эквивалентного бруса от участия в общем изгибе допускается определять без учета работы бетона растянутой зоны по формуле
N = 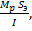
где 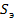 - статический момент приведенной площади поперечного сечения рассматриваемого элемента относительно нейтральной оси эквивалентного бруса;
- статический момент приведенной площади поперечного сечения рассматриваемого элемента относительно нейтральной оси эквивалентного бруса;
I – момент инерции приведенной площади поперечного сечения эквивалентного бруса, подсчитанный при упругой работе материала.
Наибольшие касательные напряжения в вертикальных элементах эквивалентного бруса (бортах и продольных переборках) определяются по формуле
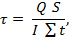
где S – статический момент части приведенного сечения эквивалентного бруса, расположенной по одну сторону от нейтральной оси, взятый относительно нейтральной оси эквивалентного бруса;
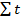 – сумма толщин бортов и продольных переборок на уровне нейтральной оси эквивалентного бруса.
– сумма толщин бортов и продольных переборок на уровне нейтральной оси эквивалентного бруса.
Для однопалубных судов с плоским одинарным днищем наибольшее касательное напряжение определяется по следующей приближенной формуле
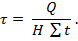
Расчетные нагрузки при расчетах местной прочности корпуса судна.
За расчетную нагрузку на днищевое перекрытие корпусов железобетонных судов принимается равномерно распределенное давление воды, кПа, уменьшенное на величину давления от веса плиты и определяемое по формулам
• в грузу 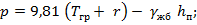
• порожнем 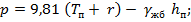
• в балласте 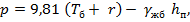
где 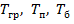 - осадка судна в состоянии в грузу, порожнем, в балласте;
- осадка судна в состоянии в грузу, порожнем, в балласте;
r – половина высоты расчетной волны;
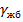 - объемный вес железобетона,
- объемный вес железобетона, 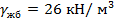 ;
;
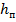 - толщина плиты, м.
- толщина плиты, м.
При расчете рамного, холостого набора и обшивки борта давление воды на борта считают распределенной по высоте борта по треугольнику или трапеции при максимальном напоре на уровне основной линии
• в грузу при 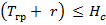 (по треугольнику)
(по треугольнику) 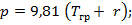
• в грузу при 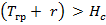 (по трапеции)
(по трапеции) 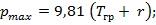
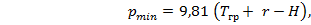
где 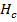 – высота борта судна, м.
– высота борта судна, м.
Расчетное давление на прочные непроницаемые переборки распределено по треугольнику или трапеции. Давление на уровне днища равно
• для переборки форпика 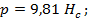
• для остальных переборок 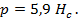
Расчетное давление на палубы
• открытые, не предназначенные для размещения груза р = 5 кПа;
• закрытых участков палуб, предназначенных для размещения пассажиров и экипажа р =3,5 кПа;
• для верхних палуб, недоступных для пассажиров и не предназначенных для грузов
р = 1 кПа.
При определении усилий от местного изгиба за расчетный пролет балок и плит принимают расстояние между осями опор.
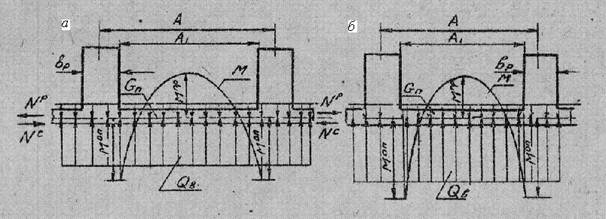
Прямоугольные плиты, опирающуюся по трем или четырем кромкам на балки и имеющей отношение сторон больше 2, рассчитывают как балку – полоску единичной ширины, вырезанной вдоль короткой кромки плиты (рис. 7.4). При отношении сторон меньшем или равном 2 расчет внутренних силовых факторов выполняют по формулам тонкой изотропной плиты.
|
Рис. 7.4 – Нагрузки и усилия, действующие на плиту: а - при поперечной системе набора, б - при продольной системе набора;
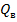 - нагрузка от давления воды; - нагрузка от давления воды; 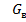 - собственный вес плиты - собственный вес плиты
|
Для неразрезных балок и балочных плит за расчетный опорный момент принимается момент в сечении по грани ребра, являющегося опорой. Наибольшие изгибающие моменты для плиты с отношением сторон больше 2 определяются по следующим формулам:
опорный момент 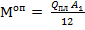 ;
;
пролетный момент 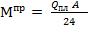 ;
;
где А – пролет плиты, равный расстоянию между осями балок;
А1 – пролет плиты в свету, А1 = А - 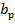 ;
;
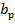 - ширина ребра;
- ширина ребра;
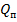 - нагрузка на плиту единичной ширины b = 1 м, длины А, определяемая по выражению
- нагрузка на плиту единичной ширины b = 1 м, длины А, определяемая по выражению
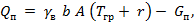
здесь 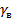 - удельный вес воды,
- удельный вес воды, 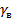 = 9,81 кН/м3;
= 9,81 кН/м3;
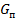 – собственный вес плиты,
– собственный вес плиты, 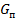 =
= 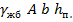
Нагрузка, приходящаяся на один пролет балки, определяется по формуле
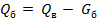 ,
,
где 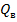 - нагрузка от давления воды,
- нагрузка от давления воды, 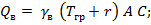
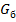 - нагрузка от весе балки,
- нагрузка от весе балки, 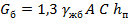 ;
;
С – пролет балки, равный расстоянию между осями опор.
Для однопалубных судов с плоским одинарным днищем осевые усилия ( 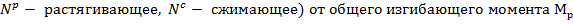 определяются по формуле
определяются по формуле
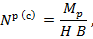
где H – высота борта судна на мидель - шпангоуте до верхней расчетной палубы;
B – ширина по конструктивной ватерлинии на мидель - шпангоуте.
Величина эксцентриситета в опорном 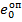 и пролетном
и пролетном 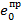 сечениях плиты определяется по выражениям
сечениях плиты определяется по выражениям
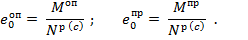
7.3.2 Расчет прочности по нормальным и наклонным сечениям 
Прочность по нормальным сечениям проверяют на действие изгибающих моментов и продольных сил по наиболее нагруженным сечениям элементов или сечениям, где изменяются площади продольных связей. Расчет выполняется по методу разрушающих усилий.
Общий порядок оценки прочности сводится к следующему:
• определяются величины и характер действующих внешних нагрузок;
• вычисляют значения наибольших усилий в связях корпуса, вызванных этими нагрузками;
• находят величины разрушающих усилий в соответствующих связях;
• определяют фактический коэффициент запаса прочности, равный отношению разрушающего усилия к усилию, вызванному расчетной нагрузкой; фактический коэффициент запаса прочности должен быть не менее установленного нормами коэффициента запаса.
Общую прочность корпуса в целом не проверяют, а определяют усилия от общего изгиба в основных продольных связях корпуса, которые суммируют с усилиями от местных нагрузок, далее оценивают прочность каждой связи в отдельности. Все конструкции, проходящие проверку на прочность, необходимо дополнительно проверять на трещиностойкость при действии расчетных эксплуатационных нагрузок.
В расчетах отдельно следует рассматривать следующие сочетания:
• сумма постоянных нагрузок;
• сумма постоянных и случайных нагрузок;
• сумма постоянных и аварийных нагрузок.
Прочность нормального сечения в рассматриваемом сочетании нагрузок обеспечена при выполнении условий:
• при действии изгибающих моментов
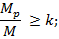
• при действии продольных сил, а также при совместном действии изгибающих моментов и продольных сил
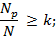
где 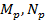 – расчетные значения разрушающего изгибающего момента, разрушающей продольной силы;
– расчетные значения разрушающего изгибающего момента, разрушающей продольной силы;
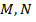 –изгибающий момент, продольная сила от расчетных нагрузок;
–изгибающий момент, продольная сила от расчетных нагрузок;
k – коэффициент запаса прочности; для элементов, участвующих в обеспечении общей и местной прочности и действии постоянной и случайной нагрузок, k = 1,8; при действии аварийных нагрузок k = 1,4.
Проверка прочности по наклонным сечениям действие перерезывающей силы обеспечена при выполнении условий:
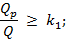
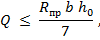
где 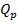 - расчетная разрушающая поперечная сила;
- расчетная разрушающая поперечная сила;
Q – поперечная сила от расчетной нагрузки;
k1 – коэффициент запаса прочности; для элементов, участвующих в обеспечении общей и местной прочности и действии постоянной и случайной нагрузок, k1 = 2,5; при действии аварийных нагрузок k1 = 2,0.
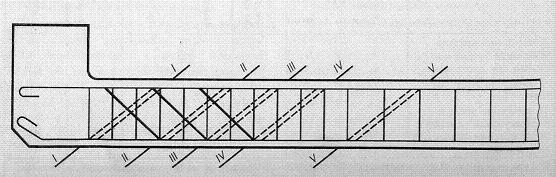
Проверка прочности на действие перерезывающей силы должна быть выполнена по нескольким наклонным сечениям (рис. 7.5):
|
| Рис. 7.5 – Расчетные наклонные сечения балки |
• сечение в месте действия наибольшей перерезывающей силы;
• сечение в месте резкого изменения поперечного сечения элемента;
• сечение I – I, проходящее через грань опоры;
• сечения II – II, III – III, IV – IV, проходящие через расположенные в растянутой зоне начала отгибов;
• сечения, проходящее через расположенные в растянутой зоне точки изменения интенсивности поперечного армирования (V – V).
При проверке прочности бортов и продольных переборок на действие перерезывающей силы от общего изгиба должны выполняться следующие условия:
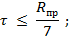
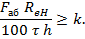
7.3.3 Определение разрушающих усилий
7.3.3.1 Расчетные разрушающие усилия в центрально сжатых элементах определяются по формуле
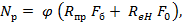
где 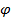 - коэффициент продольного изгиба, с помощью которого учитывается снижение несущей способности гибких элементов,
- коэффициент продольного изгиба, с помощью которого учитывается снижение несущей способности гибких элементов, 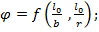
здесь 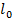 =
= 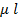 - расчетная длина сжатого элемента, определяемая умножением геометрической длины l на коэффициент приведения μ, зависящий от степени защемления и подвижности концов стержня: μ = 0,7 при полном защемлении одного конца и шарнирно неподвижном закреплении другого конца; μ = 1,0 при шарнирно – неподвижном закреплении обоих концов; μ = 2,0 при одном полность защемленном и одном свободном конце;
- расчетная длина сжатого элемента, определяемая умножением геометрической длины l на коэффициент приведения μ, зависящий от степени защемления и подвижности концов стержня: μ = 0,7 при полном защемлении одного конца и шарнирно неподвижном закреплении другого конца; μ = 1,0 при шарнирно – неподвижном закреплении обоих концов; μ = 2,0 при одном полность защемленном и одном свободном конце;
b – наименьший размер прямоугольного поперечного сечения элемента;
r – наименьший радиус сечения элемента (без учета арматуры;
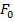 - площадь поперечного сечения всей продольной арматуры.
- площадь поперечного сечения всей продольной арматуры.
7.3.3.2 Расчетные разрушающие усилия в центрально растянутых элементах определяются по формуле
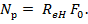
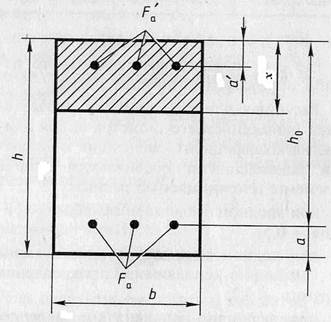
7.3.3.3 Расчетный разрушающий момент в изгибаемых элементах прямоугольного
сечения (рис. 7.6) определяется по формуле
|
| Рис. 7.6 – Расчетная схема для определения Мр в элементах прямоугольного сечения: h – высота сечения, b – ширина сечения. |
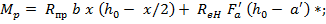
где 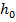 - рабочая высота сечения,
- рабочая высота сечения, 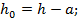
a – расстояние от центра тяжести площади поперечного сечения 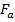 растянутой продольной арматуры до ближайшей кромки сечения;
растянутой продольной арматуры до ближайшей кромки сечения;
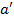 - расстояние от центра тяжести площади поперечного сечения
- расстояние от центра тяжести площади поперечного сечения 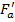 сжатой арматуры до ближайшей кромки сечения;
сжатой арматуры до ближайшей кромки сечения;
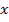 - высота сжатой зоны сечения, определяемая по формуле
- высота сжатой зоны сечения, определяемая по формуле
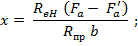
граничные условия при определении высоты сжатой зоны бетона: 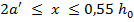 ,
,
при выполнении условия
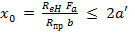 ,
,
площадь сжатой арматуры в формуле (*) 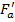 принимается равной нулю (
принимается равной нулю ( 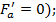
при 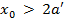 площадь сжатой арматуры в формуле (*)
площадь сжатой арматуры в формуле (*) 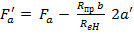 .
.
Расчетные разрушающие моменты в изгибаемых элементах таврового сечения с присоединенным пояском в растянутой зоне определяют как для прямоугольных элементов с шириной, равной ширине ребра.
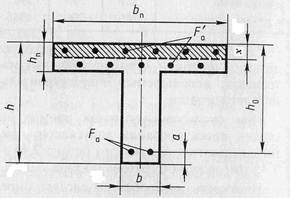
7.3.3.4 Расчетные разрушающие моменты в изгибаемых элементах таврового сечения с присоединенным пояском в сжатой зоне (рис. 7.7) при выполнении условия
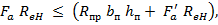
где 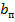 - ширина присоединенного пояска;
- ширина присоединенного пояска;
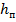 - толщина присоединенного пояска;
- толщина присоединенного пояска;
определяются как для прямоугольного сечения (рис.6) с размерами 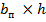 , где h – высота сечения. С незначительной ошибкой в безопасную сторону разрушающий момент можно определить по формуле
, где h – высота сечения. С незначительной ошибкой в безопасную сторону разрушающий момент можно определить по формуле
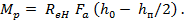
|
Рис. 7.7 – Расчетная схема для определения Мр в элементах таврового сечения при
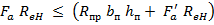
|
7.3.3.5 Расчетные разрушающие силы во внецентренно сжатых элементах
Элементы, подвергающиеся совместному воздействию осевых сил N и изгибающих моментов M, рассчитываются как внецентренно сжатые или внецентренно растянутые. Эксцентриситет силы относительно центра тяжести геометрического сечения элемента определяется по формуле
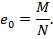
Эксцентриситет 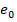 перемещает осевую силу относительно центра тяжести сечения в направлении наибольших суммарных напряжений от силы N и момента M.
перемещает осевую силу относительно центра тяжести сечения в направлении наибольших суммарных напряжений от силы N и момента M.
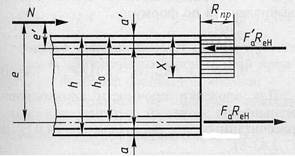
Расчетные разрушающие силы 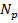 во внецентренно сжатых элементах с большим эксцентриситетом (рис. 8), удовлетворяющих условию
во внецентренно сжатых элементах с большим эксцентриситетом (рис. 8), удовлетворяющих условию 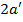
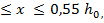 определяются по формуле
определяются по формуле
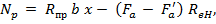
где x – высота сжатой зоны бетона, определяемая по формуле
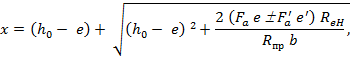
во втором слагаемом подкоренного выражения знак минус принимается в том случае, когда сила 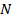 приложена за пределами центров тяжести арматуры
приложена за пределами центров тяжести арматуры 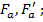
Приведенные на рис.7.8 величины 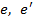 равны расстоянию от силы N до центров тяжести арматуры
равны расстоянию от силы N до центров тяжести арматуры 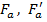 и вычисляются по ниже приведенным формулам.
и вычисляются по ниже приведенным формулам.
|
Рис. 7.8 – Расчетная схема для определения разрушающей силы 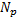 во внецентренно сжатых элементах с большим эксцентриситетом во внецентренно сжатых элементах с большим эксцентриситетом 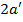 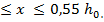
|
Расстояние от точки приложения силы N до центра тяжести арматуры 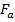 определяется по формуле
определяется по формуле
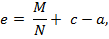
где M, N – расчетные нагрузки- изгибающий момент, сила;
с – расстояние от центра тяжести геометрического сечения до растянутой или наименее сжатой грани (для плит с = 0,5 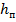 );
);
a – расстояние от центра тяжести сечения растянутой арматуры до растянутой или наименее сжатой кромки бетона.
Расстояние от точки приложения силы N до центра тяжести арматуры 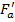 определяется по формулам
определяется по формулам
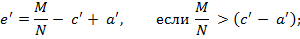
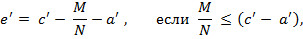
где 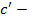 расстояние от центра тяжести геометрического сечения до сжатой или наиболее сжатой кромки (для плит с = 0,5
расстояние от центра тяжести геометрического сечения до сжатой или наиболее сжатой кромки (для плит с = 0,5 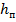 );
);
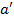 - расстояние от центра тяжести сечения сжатой арматуры до сжатой или наиболее сжатой кромки бетона.
- расстояние от центра тяжести сечения сжатой арматуры до сжатой или наиболее сжатой кромки бетона.
Влияние гибкости при расчете внецентренно сжатых элементов учитывается путем умножения эксцентриситета 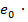 h при гибкости
h при гибкости 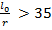 для сечений любой формы, при гибкости
для сечений любой формы, при гибкости 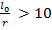 для сечений прямоугольной формы.
для сечений прямоугольной формы.
Коэффициент h для сечений прямоугольной формы определяется по формуле
h = 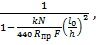
где 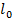 - расчетная длина элемента;
- расчетная длина элемента;
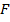 - площадь всего сечения элемента;
- площадь всего сечения элемента;
k – коэффициент запаса прочности.
Расчетные разрушающие силы 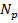 во внецентренно сжатых элементах прямоугольного сечения с малым эксцентриситетом (рис. 7.9) определяют по формулам при
во внецентренно сжатых элементах прямоугольного сечения с малым эксцентриситетом (рис. 7.9) определяют по формулам при
x > 0,55 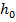
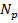 =
= 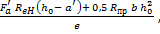
Если сила N приложена между центрами тяжести площадей поперечного сечения арматуры 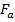 и
и 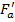 , то необходимо дополнительно определить разрушающую силу по формуле
, то необходимо дополнительно определить разрушающую силу по формуле
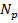 =
= 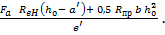
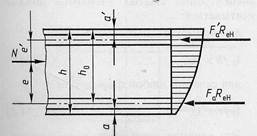
|
Рис. 7.9 – Расчетная схема для определения разрушающей силы 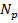 во внецентренно сжатых элементах с малым эксцентриситетом во внецентренно сжатых элементах с малым эксцентриситетом 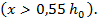
|
7.3.3.6 Расчетные разрушающие силы во внецентренно растянутых элементах
Расчетные разрушающие усилия во внецентренно растянутых элементах при малых эксцентриситетах, когда растягивающая сила N приложена между центрами тяжести площадей арматуры 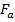 и
и 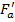 (рис. 7.10) вычисляют по формулам
(рис. 7.10) вычисляют по формулам
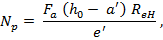
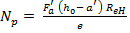 .
.
При проверке несущей способности следует использовать меньшее из двух значений 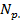
|
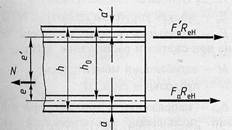
Рис. 7.10 – Расчетная схема для определения разрушающей силы 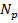 во внецентренно растянутых элементах с малым эксцентриситетом во внецентренно растянутых элементах с малым эксцентриситетом
|
Расчетные разрушающие усилия во внецентренно растянутых элементах прямоугольного сечения при больших эксцентриситетах, когда растягивающие усилия приложены вне центров тяжести площадей 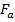 и
и 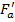 поперечных сечений арматуры (рис. 11), определяются по формулам
поперечных сечений арматуры (рис. 11), определяются по формулам
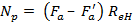 –
– 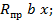
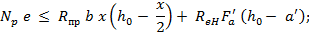
где 
здесь 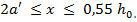
|
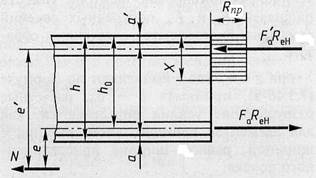
Рис. 7.11 – Расчетная схема для определения разрушающей силы 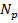 во внецентренно растянутых элементах с большим эксцентриситетом во внецентренно растянутых элементах с большим эксцентриситетом
|
7.3.3.7 Расчетная поперечная разрушающая сила 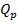 в наклонных сечениях элементов
в наклонных сечениях элементов
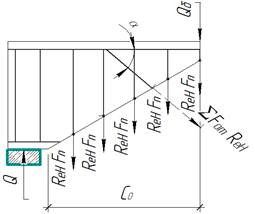
Расчетная разрушающая перерезывающая сила определяется при разрушении наклонного сечения от действия поперечных сил (рис.7.12) при предельных напряжениях в бетоне 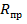 , поперечной и отогнутой арматуре
, поперечной и отогнутой арматуре 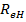 .
.
|
Рис. 7.12 – Расчетная схема для определения разрушающей перерезывающей силы 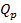
|
Расчетная разрушающая перерезывающая сила в наклонном сечении определяется по формуле
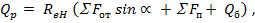
где 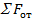 – площадь сечения всех отогнутых стержней арматуры, пересекающих наклонное сечение под углом
– площадь сечения всех отогнутых стержней арматуры, пересекающих наклонное сечение под углом 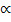 к продольной арматуре;
к продольной арматуре;
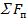 – площадь сечения всех поперечных стержней, расположенных в одной нормальной к оси элемента плоскости, пересекающей рассматриваемое наклонное сечение;
– площадь сечения всех поперечных стержней, расположенных в одной нормальной к оси элемента плоскости, пересекающей рассматриваемое наклонное сечение;
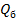 – проекция предельного усилия в бетоне наклонного сечения элемента на нормаль к оси элемента,
– проекция предельного усилия в бетоне наклонного сечения элемента на нормаль к оси элемента,
здесь 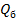 =
= 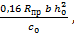
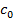 – длина проекции наименее выгодного наклонного сечения на продольную ось элемента:
– длина проекции наименее выгодного наклонного сечения на продольную ось элемента:
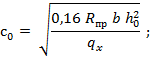
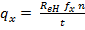 ;
;
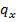 – предельная сила в поперечных стержнях (хомутах) на единицу длины элемента, Н/см;
– предельная сила в поперечных стержнях (хомутах) на единицу длины элемента, Н/см;
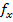 – площадь поперечного сечения одной ветви хомута;
– площадь поперечного сечения одной ветви хомута;
t - расстояние между поперечными стержнями (хомутами) по длине элемента;
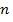 - число ветвей хомутов в одном нормальном сечении элемента.
- число ветвей хомутов в одном нормальном сечении элемента.
Расчетная разрушающая сила при отсутствии отогнутых стержней определяется по формуле
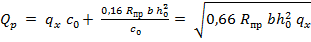 -
- 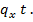
| <== предыдущая страница | | | следующая страница ==> |
| Конструкция корпуса судов из стеклопластика | | | Общие проблемы экономики |
Дата добавления: 2014-10-10; просмотров: 1150; Нарушение авторских прав

Мы поможем в написании ваших работ!