Основная теорема зубчатого зацепления

Возьмём одну пару сопряжённых зубьев в произвольном положении. В точке касания k зубьев проведём общую нормаль ТК и касательную ТТ к профилям зубьев.

Точка К₁ принадлежащая зубу ведущего колеса, будет перемещаться с окружной скоростью V₁=R₁*ω₁ вокруг центра О₁, а та же точка К₁ принадлежащая зубу ведущего колеса, будет перемещаться с окружной скоростью V₂=R₂*ω₂ вокруг центра О₂.

Отсюда следует, что

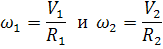
Скорости V₁ и V₂ разложим на направления ТТ и NN и получим составляющие и 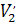а также С₁ и С₂.

Если предположим, что < 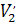, то зуб ведущего колеса должен отставать от зуба ведомого колеса, чего не может быть; если же предположить, что > 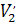, то зуб ведущего колеса будет врезаться в зуб ведомого колеса, чего не должно быть.

Следовательно остаётся единственное правильное предположение, что = .

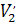Из подобных треугольников KDB и KO₁n, а также KO₂m и 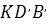со взаимно перпендикулярными сторонами следует, что

откуда

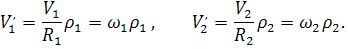
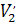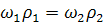Но так как = , то ; передаточное отношение .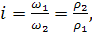

Очевидно, что передаточное отношение i будет постоянным в том случае, если будет постоянным отношение радиусов r₂ и r₁.

Эту основную теорему зубчатого зацепления можно сформулировать так: нормаль в точке контакта профилей делит линию центров на части, обратно пропорциональные угловым скоростям.

Для обеспечения постоянного передаточного отношения профили зубьев должны быть такими, чтобы общая нормаль NN в точке контакта профилей проходила через неизменную точку P на линии центров О₁О₂ и тем самым делила бы последнюю в неизменном отношении:

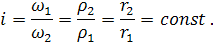
Точку P называют полюсом зацепления, а отрезок nm нормали NN – линией зацепления.

Окружности, очерченные радиусами 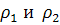, называют основными. Для построения профилей зубьев обычно используют эвольвенту и циклические кривые, в соответствии с чем различают эвольвентные и циклоидные профили зубьев.

Большинство зубчатых колёс изготовляют с эвольвентными профилями зубьев. Это объясняется рядом преимуществ эвольвентнего зацепления: возможностью некоторого отклонения от заданного межосевого расстояния без нарушения постоянства передаточного отношения, простотой изготовления зуборезного инструмента и удобством нарезания зубьев на станках.

Дата добавления: 2014-10-10; просмотров: 394; Нарушение авторских прав

Мы поможем в написании ваших работ!