
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПАССИВНЫЕ ЧЕТЫРЁХПОЛЮСНИКИ И ФИЛЬТРЫ
|
Читайте также: |
5.1. Четырёхполюсники
5.1.1. Основные теоретические положения
Четырёхполюсник (4П)– это часть электрической цепи, у которой выделены четыре зажима (полюса) для подключения к остальной схеме.
 В этой главе рассматриваются линейные пассивные четырёхполюс-ники, имеющие пару входных и пару выходных зажимов и работающие в установившемся режиме при гармоническом воздействии или в цепях постоянного тока (частный случай гармонических).
В этой главе рассматриваются линейные пассивные четырёхполюс-ники, имеющие пару входных и пару выходных зажимов и работающие в установившемся режиме при гармоническом воздействии или в цепях постоянного тока (частный случай гармонических).
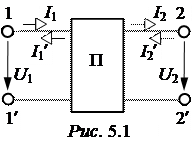
Существуют 3 режима работы пассивных четырёхполюсников (рис. 5.1):
1. Режим прямой передачи энергии: источник подключается к зажимам 1-1', а приёмник – 2-2'. Режим характеризуется системой U1, U2, I1, I2.
2. Режим обратной передачи энергии: вход – 2-2', выход – 1-1'. Режим характеризуется системой U2, U1, I2', I1'.
3. Режим питания с двух сторон. К зажимам 1-1' и 2-2' подключены источники. Режим характеризуется системой I1, U1, U2, I2'.
Четырёхполюсник может быть охарактеризован одним из следующих способов: а) параметрами одной из форм основных уравнений; б) характеристическими параметрами; в) Т- или П-схемой замещения; г) сопротивлениями холостого хода и короткого замыкания. Существуют формулы однозначного эквивалентного перехода от одного способа описания к любому другому.
Два четырёхполюсника считаются эквивалентными, если они имеют одинаковые: а) параметры одной из форм основных уравнений, или б) характеристические параметры, или в) сопротивления схем замещения, или г) параметры холостого хода и короткого замыкания.
Системы основных уравнений. В зависимости от режима питания и представляемого устройства используются 6 форм уравнений, называемых основными уравнениями четырёхполюсника и связывающих величины U1, U2, I1, I2: A, B, Z, Y, H, G-формы уравнений.
Для 1 режима используется A-форма уравнений, коэффициенты A11, A12, A21, A22 (или A, B, C, D)[1] которой есть комплексные числа с различными размерностями:
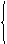
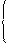
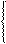 U1 = f(U2, I2), или U1 = A11·U2 + A12·I2, или U1 = A·U2 + В·I2,
U1 = f(U2, I2), или U1 = A11·U2 + A12·I2, или U1 = A·U2 + В·I2,
I1 = f(U2, I2); I1 = A21·U2 + A22·I2; I1 = С·U2 + D·I2.
Коэффициенты обладают свойством
A·В – С·D = 1 – уравнение связи.
Для режима 2 используется В-форма:
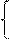
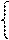 U2 = В11·U1 + В12·I1', или U2 = D·U1 + В·I1',
U2 = В11·U1 + В12·I1', или U2 = D·U1 + В·I1',
I2' = В21·U1 + В22·I1'; I2' = С·U1 + А·I1'.
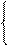 Остальные формы для третьего режима:
Остальные формы для третьего режима:
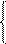
 U1 = Z11·I1 + Z12·I2', I1= Y11·U1 + Y12·U2, U1 = Н11·I1 + Н12·U2, I1 = G11·U1 + G12·I2',
U1 = Z11·I1 + Z12·I2', I1= Y11·U1 + Y12·U2, U1 = Н11·I1 + Н12·U2, I1 = G11·U1 + G12·I2',
U2 = Z21·I1+ Z22·I2', I2' = Y21·U1+ Y22·U2; I2' = Н21·I1 + Н22·U2; U2= G11·U1 + G12·I2'.
В учебниках приводятся формулы по которым осуществляется переход от коэффициентов одной формы к коэффициентам любой другой формы. Чаще используется А-форма.
Характеристические параметры четырёхполюсника включают:
1. Характеристическое (волновое) сопротивление со стороны входных зажимов: Z1С = 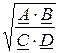 =
= 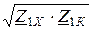 .
.
2. Характеристическое (волновое) сопротивление со стороны выходных зажимов: Z2С = 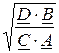 =
= 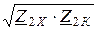 .
.
3. Постоянную передачи Г = 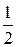 ln
ln 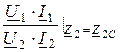 = ln
= ln 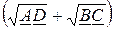 ,
,
причём Г = a + jb (Г = A + jB, g = a + jb) и
коэффициент затухания (постоянная ослабления) a измеряется в неперах (Нп), а коэффициент фазы (постоянная фазы) b – в рад или град.
Основные уравнения четырёхполюсника с характеристическими параметрами имеют следующую редакцию:
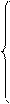 U1=
U1= 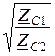 ×(U2×chГ + ZС2×I2×shГ) = A×U2 + В×I2;
×(U2×chГ + ZС2×I2×shГ) = A×U2 + В×I2;
I1= 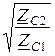 ×(
×( 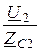 ×shГ + I2×chГ) = С×U2 + D×I2,
×shГ + I2×chГ) = С×U2 + D×I2,
откуда для прямого питания Z1X = 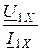 =
= 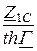 , Z1К =
, Z1К = 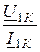 = Z1С ×thГ,
= Z1С ×thГ,
для обратного питания Z2X = 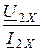 =
= 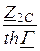 , Z2К =
, Z2К = 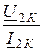 = Z2С ×thГ,
= Z2С ×thГ,
thГ = 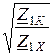 =
= 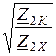 =
= 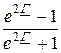 . Тогда e 2Г =
. Тогда e 2Г = 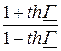 = M×e jm = e 2а×e j2b
= M×e jm = e 2а×e j2b
и а = 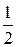 lnM, b =
lnM, b = 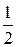 m.
m.
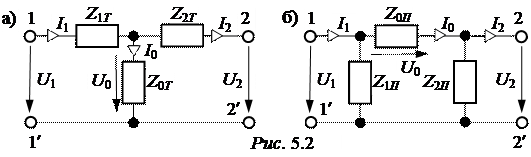 |
Т- (рис. 5.2,а) и П-схемы (рис. 5.2,б) – основные эквивалентные схемы замещения четырёхполюсников. Связь между сопротивлениями схем замеще-ния и коэффициентами А-формы следующая:
A21 = Y0Т, A22 = 1 + Z2Т ·Y0Т, A11 = 1 + Z1Т ·Y0Т, A12 = Z1Т + Z2Т + Z1Т ·Z2Т ·Y0Т;
Z0Т = 1/A21, Z1Т = 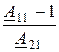 , Z2Т =
, Z2Т = 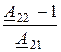 ;
;
A12 = Z0П, A11 = 1 + Z0П ·Y2П, A22 = 1 + Z0П ·Y1П, A21 = Y1П + Y2П + Z0П ·Y1П ·Y2П;
Z0П = A12, Z2П = 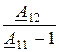 , Z1П =
, Z1П = 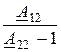 .
.
Сопротивления прямого холостого хода и короткого замыканияZ1Х и Z1К и сопротивления обратного холостого хода и короткого замыкания Z2Х и Z2К четырёхполюсника связаны с коэффициентами А-формы следующим образом:
Z1Х = 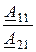 , Z1К =
, Z1К = 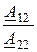 , Z2Х =
, Z2Х = 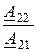 , Z2К =
, Z2К = 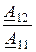 .
.
Отсюда важное соотношение 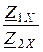 =
= 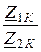 .
.
А11 = 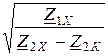 или А11 =
или А11 = 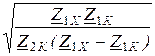 ;
;
А12 = Z2К ×А11; А21 = А11/Z1Х ; А22 = (Z2Х/Z1Х )×А11.
Входные сопротивления четырёхполюсника:
1. Со стороны входа
Z1вх = 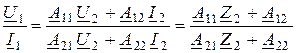 , где Z2 =
, где Z2 = 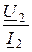 .
.
2. Со стороны выхода
Z2вх = 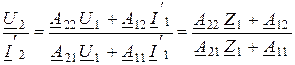 , где Z1 =
, где Z1 = 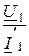 .
.
У симметричного четырёхполюсника
A11 = A22; Z1Х = Z2Х ; Z1К = Z2К ; Z1С = Z2С.
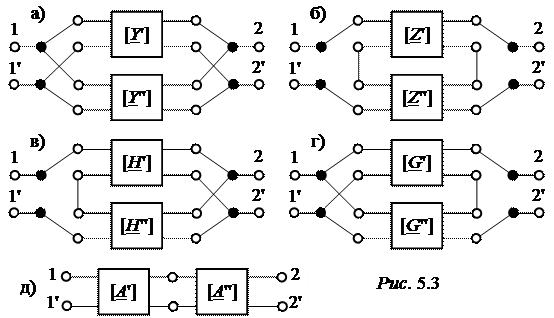
Схемы соединения четырёхполюсников показаны на рис. 5.3:
а) параллельное, при этом матричное уравнение параметров сложного 4П:
[Y] = [Y'] + [Y''];
б) последовательное, при этом [Z] = [Z'] + [Z''];
в) последовательно-параллельное, [H] = [H'] + [H''];
г) параллельно-последовательное, [G] = [G'] + [G''];
д) каскадное, [A] = [А']·[А''].
Комплексной передаточной функцией (КПФ) Н(jw) (или W(jw))называется отношение комплексных амплитуд (или действующих значений) электрических величин на выходе и входе четырёхполюсника:
Н(jw) = 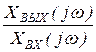 = Н(w)×е jj(w) = B(w) + jM(w).
= Н(w)×е jj(w) = B(w) + jM(w).
В электросвязи, телевидении, в теории автоматического управления
четырёхполюсники работают в широком диапазоне частот, поэтому КПФ рассматривают как функции частоты, то есть как частотные характеристики звена или системы. В связи с этим различают:
- Н(jw) – амплитудно-фазовая частотная характеристика (АФЧХ),
- Н(w) = |Н(jw)| – амплитудная частотная характеристика (АЧХ),
- j(w) – фазовая частотная характеристика (ФЧХ),
- B(w) – вещественная частотная характеристика,
- M(w) – мнимая частотная характеристика.
- годограф вектора Н(jw) на комплексной плоскости – диаграмма Найквиста.
Обычно характеристики строят в логарифмическом масштабе, для чего выражение передаточной функции логарифмируют:
lgН(jw) = lg[Н(w)×е jj(w)] = lgН(w) + jj(w)lgе.
 |
При этом выделяют логарифмическую амплитудную частотную характеристику (ЛАЧХ) L(w) = 20lgН(w) дБ, которую строят в масштабе L(w) = f1(lgw), и логарифмическую фазовую частотную характеристику (ЛФЧХ) как j(w) = f2(lgw), причём логарифмические характеристики строят как асимптотические (отрезки прямых).
| <== предыдущая страница | | | следующая страница ==> |
| Тема 15. Магматические образования Севро-Припятского плеча | | | Уравнения пассивных четырёхполюсников с коэффициентами |
Дата добавления: 2014-10-10; просмотров: 460; Нарушение авторских прав

Мы поможем в написании ваших работ!