
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уравнения пассивных четырёхполюсников с коэффициентами
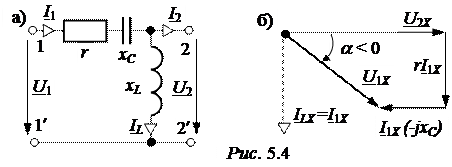 |
Задача 5.1. Рассчитать ABCD–коэффициенты Г-схемы четырёхпо-люсника (рис. 5.4,а), если r = 10 Ом, xС = 10 Ом, xL = 20 Ом. Используя основные уравнения четырёхполюсника, определить входное сопротивление Z1ВХ при нагрузке Z2 = r2 = 20 Ом.
Решение
 Способ 1. Рассматривается схема, нагруженная произвольным сопротивлением Z2, когда напряжение U2 и ток I2 отличны от нуля. Полученная схема описывается системой уравнений Кирхгофа. Методом подстановки избавляются от промежуточных токов и напряжений, приводя систему уравнений к виду: U1 = А·U2 + В·I2;
Способ 1. Рассматривается схема, нагруженная произвольным сопротивлением Z2, когда напряжение U2 и ток I2 отличны от нуля. Полученная схема описывается системой уравнений Кирхгофа. Методом подстановки избавляются от промежуточных токов и напряжений, приводя систему уравнений к виду: U1 = А·U2 + В·I2;
I1 = С·U2 + D ×I2.
При произвольной нагрузке в схеме рис. 5.4,а три неизвестных тока: I1, I2, IL. По первому закону Кирхгофа I1 = IL + I2,
по второму закону Кирхгофа U2 – IL×jxL = 0,
I1×(r – jxС ) + U2 = U1.
Из этих уравнений получаем: I1 = I2 +  = С·U2 + D·I2,
= С·U2 + D·I2,
откуда С =  =
= 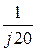 = -j0,05 См, D = 1;
= -j0,05 См, D = 1;
U1 = U2×(1 + 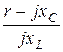 ) + I2×(r – jxС ) = А·U2 + В·I2.
) + I2×(r – jxС ) = А·U2 + В·I2.
откуда А = 1 + 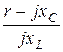 = 1 +
= 1 + 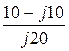 = 0,5 – j0,5 = 0,5
= 0,5 – j0,5 = 0,5 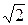 ·е -j·45°,
·е -j·45°,
В = r – jxС = 10 – j10 = 10 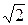 ·е -j·45° Ом,
·е -j·45° Ом,
Способ 2. Коэффициенты рассчитываются по уравнениям Кирхгофа для режимов холостого хода и короткого замыкания четырёхполюсника, когда основные уравнения принимают вид:
 холостой ход U1Х = А·U2Х ; короткое замыкание U1К = В·I2К ;
холостой ход U1Х = А·U2Х ; короткое замыкание U1К = В·I2К ;
I1Х = С·U2Х ; I1К = D ·I2К .
По схеме рис. 5.4,а, соответственно, получаем:
I1Х = 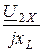 = С·U2Х ; U1Х = I1Х ×(r – jxС) + U2Х = U2Х ×(1 +
= С·U2Х ; U1Х = I1Х ×(r – jxС) + U2Х = U2Х ×(1 + 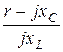 ) = А·U2Х ;
) = А·U2Х ;
I1К = I2К = D ·I2К ; I1К ×(r – jxС) = U1К = В·I2К = I2К ×(r – jxС).
Результаты расчёта коэффициентов совпали с ранее полученными.
Способ 3. Расчёт коэффициентов осуществим по сопротивлениям холостого хода и короткого замыкания четырёхполюсника (рис. 5.4,а):
Z1Х = r – jxС + jxL = 10 – j10 + j20 = 10 + j10 = 10 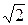 ·е j·45° Ом;
·е j·45° Ом;
Z1К = r – jxС = 10 – j10 = 10 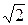 ·е -j·45° Ом;
·е -j·45° Ом;
Z2Х = jxL = j20 = 20×е j·90° Ом;
Z2К = 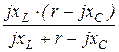 =
= 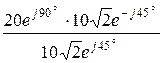 = 20 Ом.
= 20 Ом.
Из основных уравнений для режимов холостого хода и короткого замыкания
Z1Х = А/С, Z2Х = D/С, Z1К = В/D, Z2К = В/А.
Выбирая любые три соотношения с учётом свойства коэффициентов
А∙D – В∙С = 1, получаем сначала один из коэффициентов, а затем через выбранные три соотношения определяем остальные коэффициенты. Например, А = 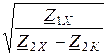 =
= 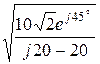 .
.
Комплексное число, стоящее в знаменателе, можно в показательной форме записать двояко:
1) j20 – 20 = 20 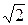 ·е j·135°; 2) j20 – 20 = 20
·е j·135°; 2) j20 – 20 = 20 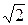 ·е -j·225°.
·е -j·225°.
Соответственно, получаем 2 значения коэффициента А:
А1 = 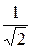 е -j·45°; А2 =
е -j·45°; А2 = 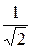 е j·135°.
е j·135°.
Коэффициент А является в общем случае комплексным числом, которое в показательной форме имеет выражение А = а·е ja.
Модуль коэффициента а = 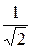 определяется однозначно. А для аргумента a получаем два значения:
определяется однозначно. А для аргумента a получаем два значения:
отрицательное a = a1= -45°, положительное a = a2= +135°.
Отбор единственного значения a произведём на основании векторной диаграммы цепи (рис. 5.4,б) для режима холостого хода четырёхполюсника, когда U1Х = А·U2Х = а·е ja·U2Х .
По векторной диаграмме получаем a < 0, тогда А = 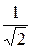 е -j·45°;
е -j·45°;
В = Z2К∙А = 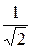 е -j·45°×20 = 10
е -j·45°×20 = 10 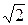 ·е -j·45° Ом;
·е -j·45° Ом;
С = 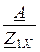 =
= 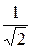
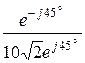 = -j0,05 См;
= -j0,05 См;
D = Z2Х∙С = 20·е j·90°(-j0,05) = 1.
Входное сопротивление четырёхполюсника при произвольной нагрузке Z2 :
Z1 = 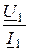 =
= 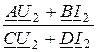 =
= 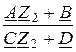 =
= 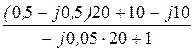 =
= 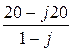 = 20 Ом.
= 20 Ом.
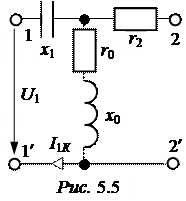 Задача 5.2. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника, собран-ного по Т-схеме (рис. 5.5), если
Задача 5.2. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника, собран-ного по Т-схеме (рис. 5.5), если
х1 = 40 Ом, r2 = 10 Ом, r0 = х0 = 40 Ом.
Используя основные уравнения четырёхполюс-ника в форме А, определить ток I1К на входе при закороченных выходных зажимах, если U1 = 100 В.
Ответ: А = -j; В = -j50 Ом;
С = 0,025 – j0,025 См; D = 1,25 – j0,25; I1К = 2,55 А.
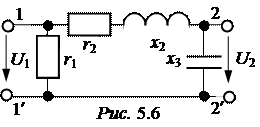 Задача 5.3. Найти элементы матри-цы [H] несимметричного четырёхполюсни-ка, собранного по П-схеме (рис. 5.6), если: r1 =10 Ом, r2 =20 Ом, x2 =20 Ом, х3 = 40 Ом. Используя основные уравнения четырёхпо-люсника в форме [H], определить напря-жение на входе при разомкнутых выходных зажимах, если U2X = 100 В.
Задача 5.3. Найти элементы матри-цы [H] несимметричного четырёхполюсни-ка, собранного по П-схеме (рис. 5.6), если: r1 =10 Ом, r2 =20 Ом, x2 =20 Ом, х3 = 40 Ом. Используя основные уравнения четырёхпо-люсника в форме [H], определить напря-жение на входе при разомкнутых выходных зажимах, если U2X = 100 В.
Ответ: H11 = 7,69 + j1,54 Ом; H12 = -H21 = 0,231 – j0,15;
H22 = -0,0231 – j0,00962 См; U1X = 50 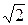 B.
B.
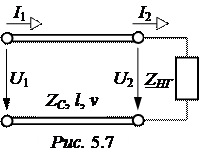 ЗАДАЧА 5.4. Для составления П-схемы заме-щения ЛЭП (рис. 5.7) и определения её входного сопротивления поставлены опыты холостого хода и короткого замыкания: U1X = 30 кВ, I1Х = 6 А, Р1Х = 27 кВт, φ1Х < 0; U1К = 4,5 кВ, I1К = 30 А, Р1К = 69 кВт, φ1К > 0.
ЗАДАЧА 5.4. Для составления П-схемы заме-щения ЛЭП (рис. 5.7) и определения её входного сопротивления поставлены опыты холостого хода и короткого замыкания: U1X = 30 кВ, I1Х = 6 А, Р1Х = 27 кВт, φ1Х < 0; U1К = 4,5 кВ, I1К = 30 А, Р1К = 69 кВт, φ1К > 0.
Определить входное сопротивление ЛЭП Z при RНГ = 1000 Ом, СНГ = 10 мкФ.
Ответ: A = D = 0,9885×е j0,53°; B = 148,3×е j59,80° Ом;
C = 0,198∙10 -3×е j81,91° См; Z1П = Z2П = 10 4×е –j81,64° Ом; Z0П = 148,3×е j59,80° Ом;
ZВХ = 986×е –j19,75° Ом.
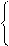 ЗАДАЧА 5.5. Известны уравнения А-формы четырёхполюсника:
ЗАДАЧА 5.5. Известны уравнения А-формы четырёхполюсника:
U1 = -j50×I2 + 1,75×U2;
I1 = 0,5×I2 – j0,0025×U2.
Требуется получить Т-схему замещения четырёхполюсника, а также записать уравнения в Н-форме.
Ответ: Z1T = j300 Ом, Z2T = -j200 Ом, Z0T = j400 Ом;
H11= - j100 Ом, H12 = 2, H21 = -2, H22 = -j0,005 См.
Задача 5.6. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника рис. 5.8,а, если хL = 80 Ом, хC = 40 Ом, r3 = r4 = 40 Ом.
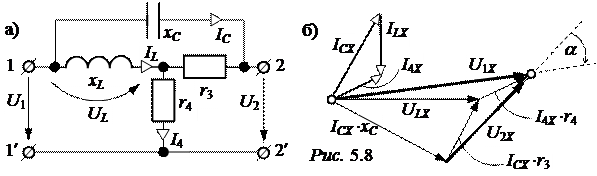 |
Используя основные уравнения четырёхполюсника, рассчитать ток нагрузки I2, если сопротивление нагрузки Z2 = 60 + j30 Ом, а напряжение на входе U1 = 220 В.
| <== предыдущая страница | | | следующая страница ==> |
| ПАССИВНЫЕ ЧЕТЫРЁХПОЛЮСНИКИ И ФИЛЬТРЫ | | | Решение. Расчёт коэффициентов выполним с помощью входных сопротивлений |
Дата добавления: 2014-10-10; просмотров: 530; Нарушение авторских прав

Мы поможем в написании ваших работ!