Реализация булевых функций в различных базисах. анализ комбинационных схем

6.1. Функционально полные системы БФ

Систему БФ {f₁, f₂, …, f_n} называют полной, если любая БФ может быть выражена суперпозицией функций f₁, f₂,…, f_n и булевых переменных. Функции, полученные применением суперпозиции, отличаются от исходных функций, и их свойства отличаются от свойств исходных функций. Среди БФ есть такие, которые обладают основными свойствами. Доказано, что число функций в полной системе не превышает четырех.

6.2. Понятие базиса

Базисом называют полную систему функций алгебры логики, с помощью которых любую БФ можно представить как суперпозицию функций базиса. Минимальный базис состоит из такого набора функций, что исключение любой из них превращает этот набор в неполную систему функций. Известны и широко применяются несколько базисов, состоящих из элементарных функций.

Базис, который называют основным, включает три функции – И, ИЛИ, Не.

1. Базис И, Не включает две функции – конъюнкцию (И) и отрицание (Не). Чтобы реализовать любую функцию в этом базисе, необходимо провести преобразование БФ. Рассмотрим пример функции 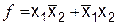. Она записана в базисе И, ИЛИ, Не.

Чтобы представить эту функцию в базисе И, Не, необходимо в исходной функции заменить операцию логического сложения на операцию логического умножения. Выполнить эти преобразования можно с использованием теоремы де Моргана:

.

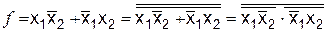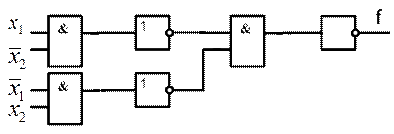
Рис. 6.1. Реализация БФ в базисе И, Не

После такого преобразования функция реализуется только с помощью операции конъюнкции и инверсии. Схема, реализующая эту функцию, представлена на рис. 6.1 и содержит только элементы И и Не, входящие в базис.

2. Базис ИЛИ, Не включает две функции – дизъюнкцию (ИЛИ) и отрицание (Не). Чтобы реализовать любую функцию в этом базисе, необходимо также провести преобразование БФ. Рассмотрим преобразования на примере той же функции. Здесь следует применить теорему Де-Моргана к конъюнкции:

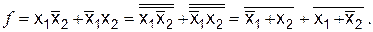
Таким образом, в окончательной формуле присутствуют только операции ИЛИ и Не. Схема, реализующая эту БФ, приведена на рис. 6.2.

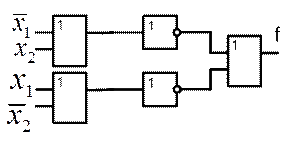
Рис. 6.2. Реализация БФ в базисе ИЛИ, Не

3. Базис И-Не включает в себя только один логический элемент. БФ этого элемента 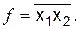На основе этого элемента производятся различные цифровые устройства. Чтобы реализовать любую функцию в этом базисе, необходимо также проводятся преобразования БФ:

.

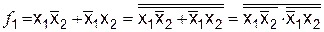Таким образом, в окончательной формуле присутствуют только операции И-Не. Схема, реализующая эту БФ, приведена на рис. 6.3.

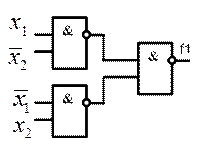
Рис. 6.3. Реализация БФ в базисе И-Не

4. Базис ИЛИ-Не включает в себя только один логический элемент и также назвается универсальным. Чтобы реализовать любую функцию в этом базисе, необходимо провести преобразования БФ:

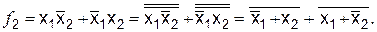
Схема, реализующая эту БФ, приведена на рис. 6.4.

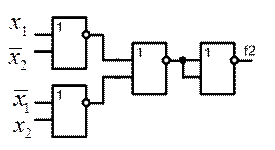
Рис. 6.4. Реализация БФ в базисе ИЛИ-Не

Рассмотрим особенности базисов И-Не и ИЛИ-Не. Элемент И-Не описывается функцией 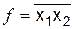. Таблица истинности этой функции приведена в табл. 6.1.

Таблица 6.1

Таблица истинности функции И-Не

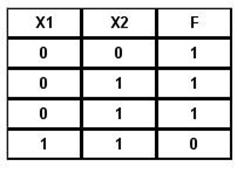
Если на оба входа элемента И-Не подать одну и ту же переменную (первая и четвертая строки таблицы), то в результате получается функция: 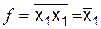, т. е. элемент И-Не становится инвертором (рис. 6.5, а). При последовательном соединении двух элементов И-Не, как показано на рис. 6.5 (б), схема выполняет функцию И. Таким образом, базис И-Не содержит как бы три элемента – И-Не, И, Не.

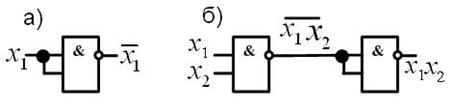
Рис. 6.5. Соединение элементов базиса И-Не:

а – инвертор (Не); б – элемент И

Элемент ИЛИ-Не описывается функцией 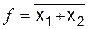. Таблица истинности этой функции приведена в табл. 6.2.

Таблица 6.2

Таблица истинности функции ИЛИ-Не

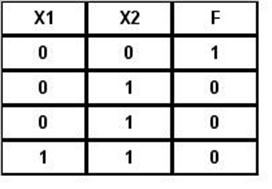
Если на оба входа элемента ИЛИ-Не подать одну и ту же переменную, то получим функцию: 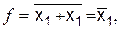т. е. элемент ИЛИ-Не становится инвертором (рис. 6.6, а). При последовательном соединении двух элементов ИЛИ-Не, как показано на рис. 6.6 (б), элемент ИЛИ-Не преобразуется в элемент ИЛИ. Таким образом, базис ИЛИ-Не содержит как бы три элемента – ИЛИ-Не, ИЛИ, Не.

Рис. 6.6. Соединение элементов базиса ИЛИ-Не:

а – инвертор (Не); б – элемент ИЛИ

Рассмотрим примеры реализации функций в различных базисах.

1. Функция D в базисе И-Не (рис. 6.7)

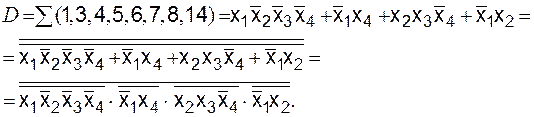
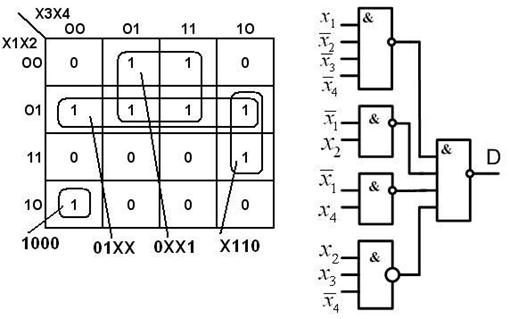
Рис. 6.7. Функция D:

а – карта Карно; б – схема в базисе И-Не

2. Функция К в базисе И-Не (рис. 6.8)

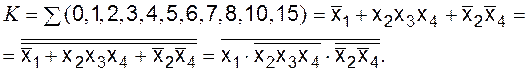
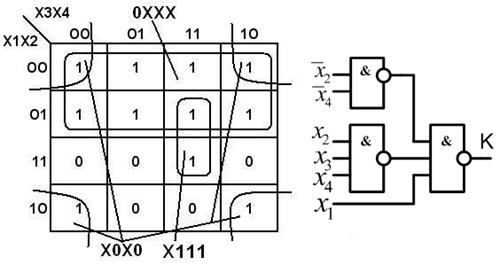
Рис. 6.8. Функция K:

а – карта Карно; б – схема в базисе И-Не

3. Функция F в базисе И-Не (рис. 6.9)

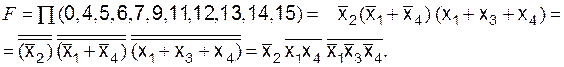
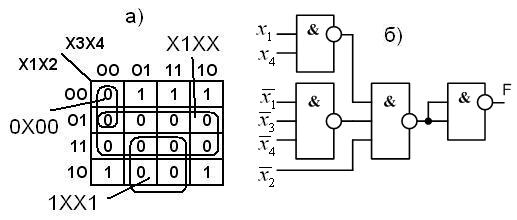
Рис. 6.9. Функция F:

а – карта Карно; б – схема в базисе И-Не

4. Функция Q в базисе И-Не (рис. 6.10)

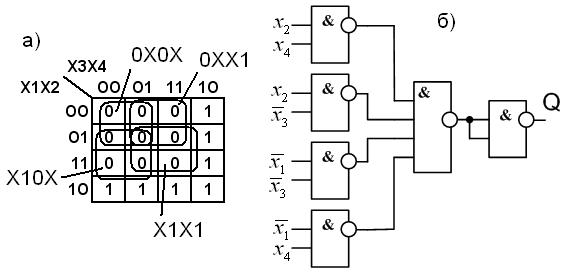
Рис. 6.10. Функция Q:

а – карта Карно; б – схема в базисе И-Не

5. Функция R в базисе ИЛИ-Не (рис. 6.11)

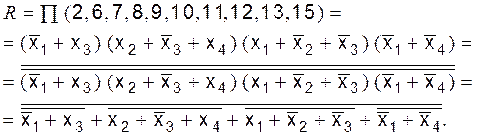
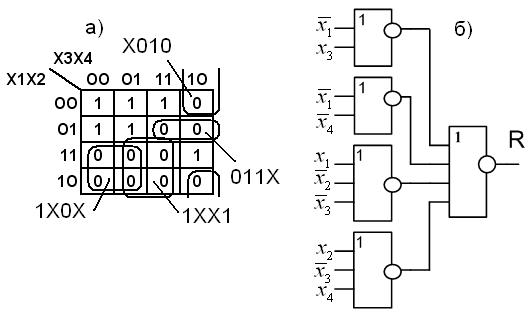
Рис. 6.11. Функция R:

а – карта Карно; б – схема в базисе ИЛИ-Не

6. Функция S в базисе ИЛИ-Не (рис. 6.12)

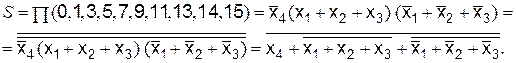
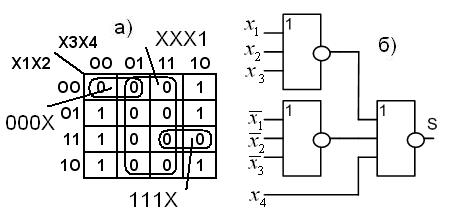
Рис. 6.12. Функция S:

а – карта Карно; б – схема в базисе ИЛИ-Не

7. Функция G в базисе ИЛИ-Не (рис. 6.13)

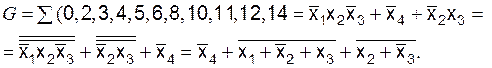
Рис. 6.13. Функция G:

а – карта Карно; б – схема в базисе ИЛИ-Не

8. Функция W в базисе ИЛИ-Не (рис. 6.14)

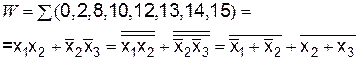
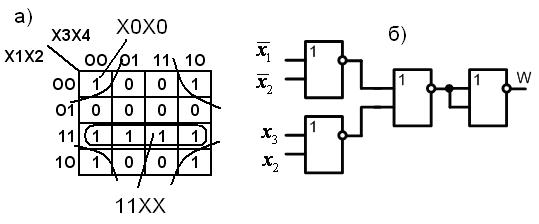
Рис. 6.14. Функция W:

а – карта Карно; б – схема в базисе ИЛИ-Не

Дата добавления: 2014-10-10; просмотров: 2567; Нарушение авторских прав

Мы поможем в написании ваших работ!