Разложение булевых функций

Любая БФ может быть преобразована к виду:

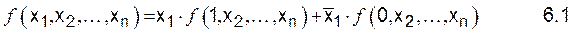
Например,

.

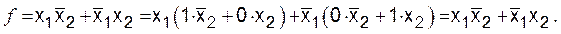В общем случае разложение может быть проведено для любого количества переменных k, где k≤n, и тогда БФ может быть представлена в виде:

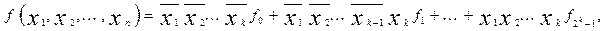
где 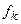– БФ, получаемая из исходной подстановкой в нее набора переменных, равного значению k. При этом можно получить БФ в форме, упорядоченной по отношению к некоторым переменным. Например, БФ можно представить так, что каждая конъюнкция функции будет зависеть от х₁ и х₂ или их инверсий даже в тех случаях, когда в конъюнкциях исходной функции они отсутствуют. Например,

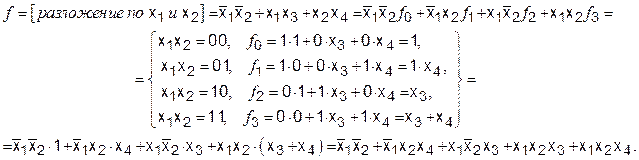
Теперь каждая конъюнкция функции зависит от х₁ и х₂. При проведении разложения по всем переменным можно получить СДНФ БФ. Разложение БФ используется в тех случаях, когда БФ должна быть представлена так, чтобы в каждой конъюнкции присутствовали необходимые переменные.

Дата добавления: 2014-10-10; просмотров: 348; Нарушение авторских прав

Мы поможем в написании ваших работ!