
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Анализ комбинационных схем
Задача анализа комбинационных схем состоит в нахождении булевой функции КС. БФ при анализе может быть представлена или в аналитической форме, или в виде таблицы истинности. Анализ проводят для того, чтобы определить функциональные свойства КС или для проверки правильности функционирования КС, или же для того, чтобы определить работоспособность схемы в режимах, отличающихся от заданных при проектировании КС. Работу устройств железнодорожной автоматики необходимо анализировать и при повреждениях некоторых его элементов. При этом важно выполнение основного требования: любое повреждение не должно приводить к изменению алгоритма функционирования, которое может нарушить условия обеспечения безопасности движения поездов.
При анализе КС важным является определение возможности упрощения КС. Этого можно достичь минимизацией и упрощением БФ. Отдельной задачей является выяснение поведения устройства в переходных режимах и нарушения работы именно в эти периоды.
Анализ КС проводят в два этапа.
1. Из имеющейся принципиальной схемы устройства удаляют все несущественные или вспомогательные элементы, которые не влияют на логику работы КС, а предназначены для обеспечения надежности или устойчивости, или дополнительных возможностей схемы. Тогда схема будет состоять только из элементов, выполняющих логические функции.
2. На основе полученной таким образом схемы записывается булева функция (в базисе И, ИЛИ, Не), которая и подвергается анализу.
При анализе контактной схемы функция в виде ДНФ записывается непосредственно по самой схеме:
1) последовательно соединенные группы контактов записываются с помощью операции И;
2) параллельно соединенные группы контактов записываются с помощью операции ИЛИ;
3) нормально-разомкнутые контакты записываются с помощью прямой переменной;
4) нормально-замкнутые контакты записываются с помощью инверсной переменной;
5) все контакты одного реле записываются под именем одной переменной;
6) БФ минимизируется;
7) проводится анализ БФ.
Для схемы, представленной на рис. 6.15 (а), запишем БФ в форме ДНФ:
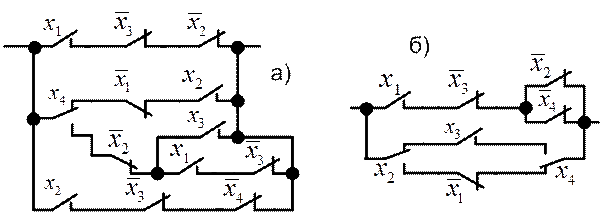
Рис. 6.15. Контактная схема
а – исходная схема; б – упрощенная схема
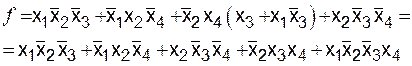
Доопределим эту ДНФ до СДНФ. Для этого каждую конъюнкцию ДНФ необходимо умножить на сумму
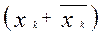 ,
,
чтобы получить конституенты единицы, где k – номер переменной, недостающей в конъюнкции.
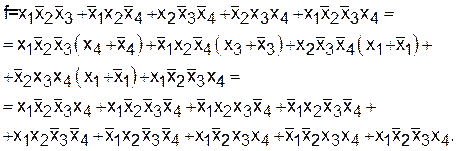
Нанесем СДНФ на карту Карно (рис. 6.16) и минимизируем. В результате минимизации получится более простая функция, схема которой показана на рис 6.15 (б).
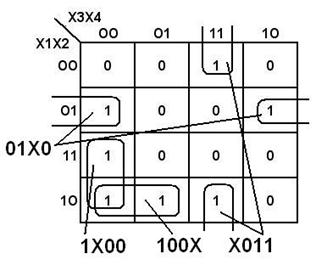
Рис. 6.16. Минимизация функции f картой Карно

При анализе схемы на электронных элементах функция также может записываться непосредственно по самой схеме. Но при сложной схеме это может оказаться затруднительным. В этом случае можно предложить следующий алгоритм:
1) выходу каждого логического элемента приписывается какое-либо имя;
2) выходная функция каждого элемента записывается в терминах переменных на ее входах;
3) последовательно от входов к выходам описывается вся схема;
4) функция преобразуется в базис И, ИЛИ, Не и представляется в ДНФ;
5) при необходимости функция доопределяется до СДНФ и минимизируется;
6) проводится анализ БФ.
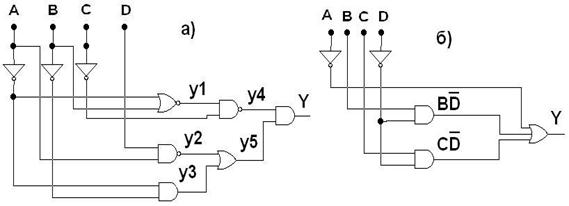
Рис. 6.17 Комбинационная схема и функция Y
а – исходная КС; б – минимизированная КС
Рассмотрим схему, приведенную на рис. 6.17 (а). Выход каждого элемента обозначен своей функцией. Запишем функцию каждого элемента, выведем БФ Y и построим схему (рис. 6.17, б):
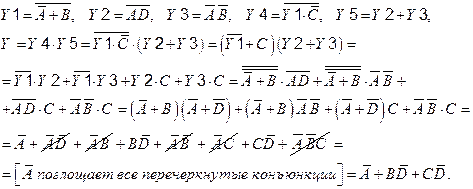
Иногда удобно закон схемы представить в виде таблицы истинности. Для этого составляют таблицу, в левой части которой записаны все возможные наборы аргументов. Затем вычисляется значение выходного сигнала схемы для каждого набора переменных и результат заносится в таблицу. При этом можно использовать следующие очевидные свойства элементов.
A. Для электронных схем:
¨ 0 на любом входе схемы И приводит к появлению 0 на выходе, независимо от сигналов на любых других входах;
¨ 1 на любом входе схемы ИЛИ приводит к появлению 1 на выходе, независимо от сигналов на любых других входах;
¨ 0 на любом входе схемы И-Не приводит к появлению 1 на выходе, независимо от сигналов на любых других входах;
¨ 1 на любом входе схемы ИЛИ-Не приводит к появлению 0 на выходе, независимо от сигналов на любых других входах.
B. Для релейных схем:
1) если контакт любого реле, стоящий в цепи последовательно соединенных контактов, оказался разомкнут, то все контакты других реле, стоящие последовательно с ним, можно не рассматривать, т. к. цепь разомкнута и значение функции этой цепочки равно 0;
2) если последовательно соединенные контакты реле, находящиеся в одной цепочке, соединяющей вход и выход схемы, оказались замкнуты, то все остальные, параллельные ей, цепи можно не рассматривать, а в таблице истинности записать значение БФ равное 1.
Например, задана КС (рис. 6.18). Составить для нее таблицу истинности.
Для решения задачи обозначим выходы элементов Z, G, F, Y и составим следующую таблицу истинности (для упрощения вычислений выход каждого элемента обозначен своей функцией и занесен в таблицу):
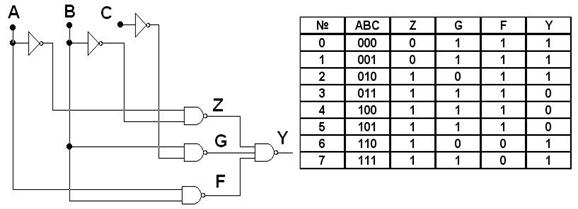
Рис. 6.18. Комбинационная схема и таблица истинности
1) функцию Z реализует элемент И-Не, на выходе которого будет 1, если А=1 или В=1 (строки со второй по 7);
2) функцию G реализует элемент И-Не, на выходе которого будет 1, если В=0 или С=1 (строки 0, 1, 4, 5, 3, 7);
3) функцию F реализует элемент И-Не, на выходе которого будет 1, если А=0 или В=0 (строки 0, 1, 2, 3, 4, 5);
4) функцию Y реализует элемент И-Не, на выходе которого будет 1 в строках, где или Z=0, или G=0, или F=0 (строки 0, 1, 2, 6, 7).
При решении таких задач промежуточные столбцы (Z, G, F) в таблице истинности могут быть опущены, а вычисление выходных сигналов производится прямо на схеме. Например, на рис. 6.19 рассмотрены состояния выхода схемы при ABC={010, 100, 101, 111}. Результат совпадает с предыдущим анализом.
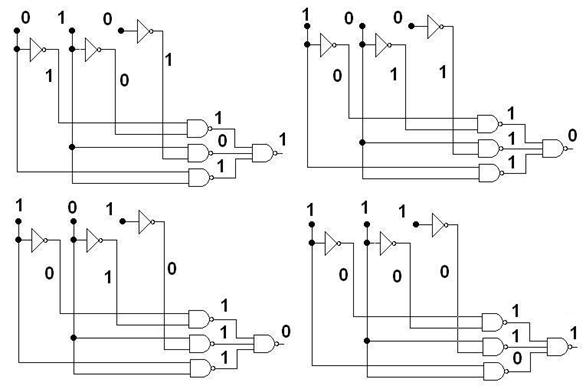
Рис. 6.19. Значения выхода схемы при различных наборах
входных переменных
Пусть задана контактная схема (рис. 6.20), для которой необходимо составить таблицу истинности. При рассмотрении схемы цепи, имеющие разомкнутые контакты, будем разрывать, а замкнутые контакты соединять проводником. Слева от каждой схемы представлены наборы аргументов в последовательности х1, х2, х3, а справа над схемой показано значение функции (рис. 6.21).
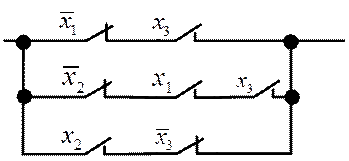
Рис. 6.20. Контактная схема
На наборах 0, 4, 7 все три параллельные цепи имеют разрывы, а значит, ток через цепь течь не может и значение функции равно 0. На наборах 1, 3 замкнута верхняя цепь, на наборах 2, 6 – нижняя, на наборе 5 – средняя. На этих наборах значение функции равно единице (табл. 6.3).
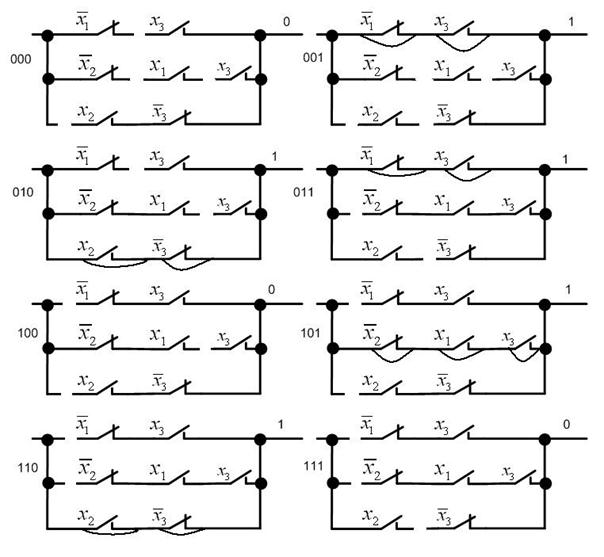
Рис. 6.21. Состояние контактов схемы при различных наборах
аргументов
Таблица 6.3
Восстановленная таблица истинности релейной схемы
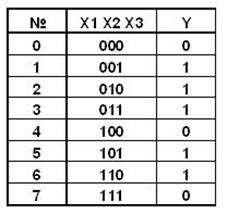
На рис. 6.22, 6.23, 6.24 приведены схемы устройств. Таблицы истинности схем сведены в табл. 6.4. Полученные функции минимизированы и построены новые схемы на основе МДНФ в различных базисах.

Рис. 6.22. Преобразование схемы:
а – исходная схема; б – минимизированная схема
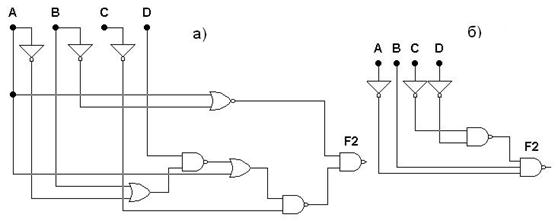
Рис. 6.23. Преобразование схемы:
а – исходная схема; б – минимизированная схема
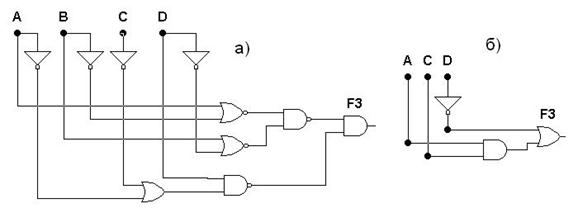
Рис. 6.24. Преобразование схемы:
а – исходная схема; б – минимизированная схема

Таблица 6.4
Таблица истинности для F1, F2, F3
| № | ||||||||||||||||
| ABCD | ||||||||||||||||
| F1 | ||||||||||||||||
| F2 | ||||||||||||||||
| F3 |
При анализе некоторых схем достаточно вывести выходную функцию, чтобы найти более короткую формулу, описывающую схему.
Например, на рис. 6.25 приведена схема устройства, для которого выведена выходная функция (выход элемента DD5). Элемент DD6 на этой схеме реализует ту же самую функцию, что и заданная схема.
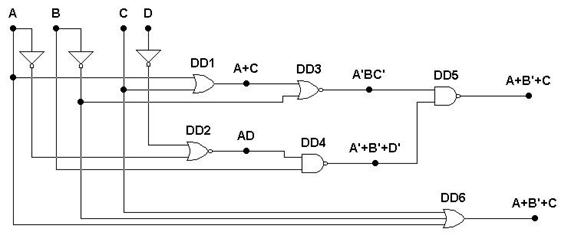
Рис. 6.25. Анализ схемы и ее минимизация
Покажем вывод выходной функции схемы:
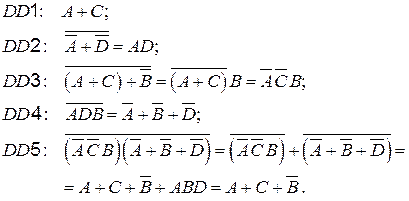
На рис. 6.26, 6.27 приведены еще две схемы, для которых приведены значения выходных функций.
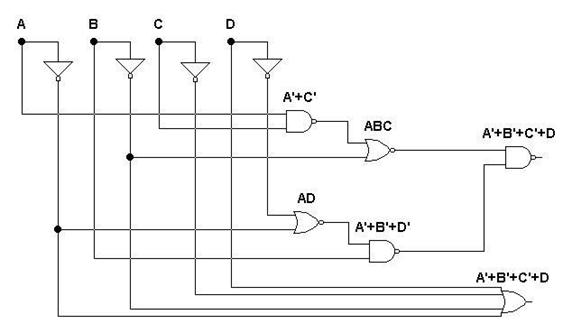
Рис. 6.26. Анализ схемы и ее минимизация
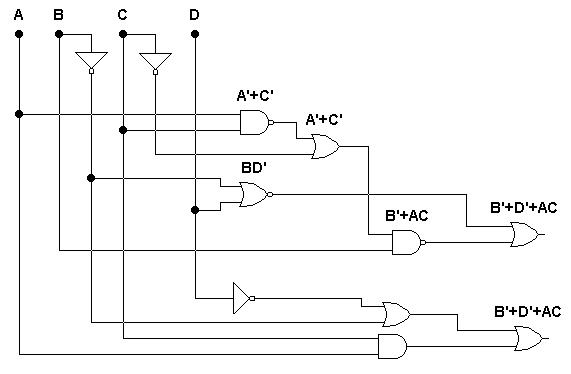
Рис. 6.27. Анализ схемы и ее минимизация
| <== предыдущая страница | | | следующая страница ==> |
| Разложение булевых функций | | | Power Point Создание однослайдовой презентации |
Дата добавления: 2014-10-10; просмотров: 652; Нарушение авторских прав

Мы поможем в написании ваших работ!