
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Математические методы при подготовке и обосновании решений в горном производстве
Г л а в а III
§3.1 Принятие решений.
После анализа в предыдущем разделе монографии возможностей использования классических методов исследования для решения современных проблем горного производства рассмотрим некоторые математические методы.
Произвольное решение во всех случаях глубоко отрицательно. Любое обоснование решения, даже в условиях риска или неопределенности, ведет к положительному эффекту. Для большей достоверности принимаемого решения следует попытаться его обосновать различными методами. Например, одну и ту же задачу несколько независимых экспертов решают различными методами, а конечный результат представляет собой среднее из рассмотренных вариантов решения.
Все чаще при подготовке решений используются методы исследования операций. Назначение этих методов - объективно разобраться в явлении или процессе, численно оценить планируемые действия и представить варианты решений, из совокупности которых ответственное лицо выберет одно единственное для преобразования его в действие. Чем сложнее планируемые мероприятия, тем менее допустимы «волевые решения» и тем важнее научные методы, позволяющие прогнозировать последствия реализации каждого решения. Цель исследования операций - предварительное обоснование оптимальных (лучших в данных условиях) решений. Задачи исследования операций делятся на прямые и обратные. Прямые задачи отвечают на вопрос, что будет, если в заданных условиях примем некоторое решение, и чему будет равен в этом случае показатель эффективности. В обратной задаче, отвечают на вопрос, что надо предпринять, чтобы критерий эффективности был максимальным (минимальным). Параметры, совокупность которых образует решение, называется элементами решения. Задача исследования операций - подготовка решения, которая возлагается на экспертов, советы, соответствующие отделы, службы, а принятие решения относится к компетенции ответственного лица.
В исследовании каждой конкретной операции, явления различают несколько этапов:
· постановка задачи, выбор цели;
· формализация ситуации и составление модели (математической, физической, интуитивно-мысленной);
· анализ модели и определение элементов решения;
· принятие решения;
· преобразование информации в действие с последующим контролем эффективности решения и, в случае необходимости, уточнением первоначальных цели и модели.
Анализ моделей проводится:
· аналитическими методами исследования экстремальных задач;
· посредством имитационного моделирования;
· методом игр и статистических решений;
· с помощью экспертных оценок и по результатам специально организованных деловых игр.
Модель принятия решений имеет несколько различных элементов: перечень целей, перечень параметров альтернатив, вероятности (если они есть) исходов принимаемых решений, критерий решений (показатель эффективности), определяющий путь нахождения лучшей альтернативы. Обычно этим способом решаются обратные задачи исследования операций.
Существуют и другие методы принятия решений. В большинстве случаев решения принимаются бессознательно в силу инстинктов, рефлексов - автоматически. Это относится, прежде всего, к прямым задачам, когда ситуация предельно ясна (поломка оборудования, разрушение коммуникаций, оползни, природные катаклизмы и др.). Основы правильности решений, ограниченных сжатыми сроками, в этом случае составляет квалификация и осведомленность работников, личные качества руководителя, принимающего решение и организующего контроль результатов действия. Интуиция (предчувствие, ощущение, догадка) зависит от опыта принимающего решение в данной области.
На втором месте по частоте применения стоит метод проб и ошибок. Его успех зависит от скорости обучения, памяти, опыта, от способности фиксировать событие, - был ли результат хорошим или плохим по отношению к цели операции. Этот метод принятия решения долог и не особенно хорош.
Следующий метод принятия решения связан с обращением к авторитету (более опытный специалист, книги, учебник). Однако, обращение к авторитету не всегда обоснованно и может означать уклонение от ответственности. Обращение к авторитету обосновано на стадии, когда готовится решение.
По числу критериев задачи принятия решений делятся на однокритериальные и многокритериальные. Однокритериальные детерминированные задачи являются более простыми с точки зрения определенности их решения. В этих задачах - цель операции, ее оценка и исход - связаны детерминированной зависимостью со стратегией оперирующей стороны. Поэтому принцип оптимальности здесь очевиден, - оптимальное решение соответствует максимуму (минимуму) критерия оптимизации.
При решении однокритериальных задач принятия решений в условиях риска или неопределенности, а также многокритериальных, возникают проблемы выбора, иерархии (относительной важности) и др. И только затем приступают к решению проблем формально-математического характера. Сложности возникают, прежде всего, от того, что не ясен сам принцип оптимальности. Главным является вопрос: какое решение следует считать оптимальным в условиях риска, неопределенности и многокритериальности задач?
Применительно к однокритериальным задачам в условиях риска и неопределенности главная проблема заключается в детерминизации случайных и неопределенных величин. Посредством замены случайных величин параметрами их распределений (математическое ожидание, дисперсия) задачу сводят к детерминированной. Сложнее вопрос выбора оптимальности применительно к многокритериальным задачам (принцип «скаляризации»). В результате решения этой проблемы многокритериальная задача, соответствующая некоторой сложной, многоцелевой операции, сводится к однокритериальной. В практике задачи «детерминизации» и «скаляризации» возникают как порознь, так и совместно в зависимости от сочетания признаков «определенность - риск - неопределенность».
В однокритериальных детерминированных задачах принятия решений предпочтительно применение аналитического исследования, так как лишь оно является наиболее полным решением. Однако, воспользоваться аналитическим исследованием задачи удается сравнительно редко из-за принципиальных трудностей решения систем уравнений математической модели, к тому же содержащей, как правило, эмпирические коэффициенты. Тем не менее, использование аналитических методов столь эффективно, что часто идут на значительные упрощения и огрубления первоначальной модели. Детерминированные математические модели, состоящие из систем уравнений (или даже всего одного уравнения) отражают наиболее важные свойства объекта, так как излишне подробное описание приводит к неразрешимости задачи. С помощью детерминированных моделей, характеризующих основные закономерности изучаемых объектов, можно определить общие свойства целой группы объектов, относящихся к одному классу явлений. Обычно в основе математических моделей лежит баланс масс, энергий, импульсов.
Например, задача о взрыве, важнейшая для горного производства, решалась многими выдающимися учеными аналитическими методами и с применением методов подобия и размерностей. Эти исследования позволили установить важнейшие закономерности этого процесса, распределение скорости, давления, плотности и температуры за фронтом ударной волны для различных термодинамических характеристик газа. Аналитически установлено, что вблизи центра взрыва возникают большие градиенты температуры, а плотность стремится к нулю, температура и энтропия к бесконечности. Закон затухания ударной волны зависит от формы заряда. Свойства вязкости и теплопроводности могут оказывать некоторое влияние на движение газа вблизи центра взрыва. При сильном взрыве можно пренебречь давлением перед ударной волной по сравнению с давлением за ударной волной. Скорость распространения ударной волны в общем случае зависит от термодинамических характеристик газа (показатель Пуассона 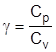 ).
).
Если же возмущение распространяется с бесконечно большой скоростью, то возможно решение без ударной волны. С использованием метода теории подобия и размерностей установлено, что применение больших сосредоточенных зарядов для подъема горной массы энергетически невыгодно по сравнению с рассредоточением зарядов. Таким образом, аналитические исследования взрыва очень важны, но для практического применения мало пригодны, так как требуют знания многих опытных коэффициентов, зависящих от характеристик породы, от свойств ВВ, газа и многих других факторов, для определения которых нужен эксперимент. Поэтому на практике часто действие взрыва характеризуют только массой ВВ, которая пропорциональна энергии взрыва, и в этом случае пренебрегают формой, химической и физической природой заряда. Это не всегда правильно, в частности, в вопросах действия кумулятивных зарядов.
В нормативной литературе [14] при расчете расстояний (r), безопасных по действию ударной волны при взрывах рекомендуется применять формулы
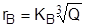 для открытых зарядов ВВ при Q>10 т (3.1)
для открытых зарядов ВВ при Q>10 т (3.1)
 для тех же условий при Q< 10 т , (3.2)
для тех же условий при Q< 10 т , (3.2)
где Q - масса заряда ВВ.
Для определения расстояний (м), при которых колебания грунта, вызываемые однократным взрывом сосредоточенного заряда ВВ, становятся сейсмически безопасными для зданий и сооружений, рекомендуется формула:
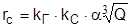 (3.3)
(3.3)
Формулы (3.1)-(3.3) эмпирические, найдены в определенных условиях и справедливы лишь для исследованных интервалов изменения переменных. Опытные коэффициенты КВ, kВ, kг, kС, α, изменяются в широком диапазоне. Так, для открытых зарядов Кв в (3.1) изменяется от 400 (отсутствие повреждений зданий) до 30-50 (полное разрушение застекления, повреждение рам и дверей). В формуле (3.2) kВ уменьшается с 50-150 (отсутствие повреждений) до 2-4 (разрушение внутренних перегородок, рам, дверей, сараев) и 1,5-2,0 (разрушение малостойких каменных и деревянных зданий). В формуле (3.3) рекомендуется [14] принимать Кг = 5 (ненарушенные скальные породы), Кг =8 (нарушенные скальные породы), Кг =12 (необводненные песчаные, глинистые грунты глубиной до 10 м).
Кг =20 (водонасыщенные грунты). Коэффициент kС изменяется от 1 (одиночные производственные здания с железобетонным и металлическим каркасом) до 2 (небольшие жилые поселки). И, наконец, α =1 - взрыв на рыхление, α = 0,8 - взрыв на выброс,
α = 0,5 - взрыв полууглубленного заряда. В случае, когда не подходит ситуация под указанные варианты, используют коэффициенты, дающие больший радиус безопасной зоны.
Как отмечалось, формулы (3.1) - (3.3) эмпирические, но и в этом случае будет получен лучший результат, если при подборе вида формулы учитывались теоретические представления о сущности происходящего процесса [5]. Применительно к рассмотренным примерам, легко убедиться, что формулы вида (3.1) и (3.3) могут быть получены из допущения пропорциональности скорости изменения действия заряда площади поражения, так как из 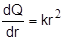 следует
следует 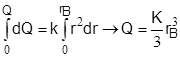 Откуда
Откуда 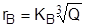
Точно также может быть получена формула (3.3). Формула (3.2) находится при условии, что
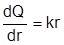
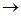
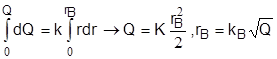 .
.
В статье [5] показаны различные случаи нахождения эмпирических формул с учетом физики процесса. Применяя тот же принцип, что и в случае (3.1)-(3.3), можно определить зависимость давления ударной волны Р от расстояния г, исходя из допущения 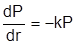 (скорость изменения давления ударной волны пропорциональна текущему значению Р). В результате инте-грирования находим экспоненциальный закон изменения Р(r). Учитывая неоднозначность ситуации из-за большой вариабельности коэффициентов пропорциональности в эмпирических формулах считаем возможным рекомендовать использовать для принятия решений (особенно в вопросах безопасности) упрощенные методы расчета последствий взрыва. Конечно, при этом следует знать, что пренебрегаем сопротивлением воздуха, допускаем аддитивность потоков энергии взрыва. До 10-15% энергии ВВ расходуется на разрушение горной массы (при заглублении ВВ). Часть энергии ВВ идет на нагрев среды (в центре) и химические реакции, какая-то часть может быть поглощена или, напротив, отражена от препятствия (стена или др.) и усилить ударную волну в одном из направлений.
(скорость изменения давления ударной волны пропорциональна текущему значению Р). В результате инте-грирования находим экспоненциальный закон изменения Р(r). Учитывая неоднозначность ситуации из-за большой вариабельности коэффициентов пропорциональности в эмпирических формулах считаем возможным рекомендовать использовать для принятия решений (особенно в вопросах безопасности) упрощенные методы расчета последствий взрыва. Конечно, при этом следует знать, что пренебрегаем сопротивлением воздуха, допускаем аддитивность потоков энергии взрыва. До 10-15% энергии ВВ расходуется на разрушение горной массы (при заглублении ВВ). Часть энергии ВВ идет на нагрев среды (в центре) и химические реакции, какая-то часть может быть поглощена или, напротив, отражена от препятствия (стена или др.) и усилить ударную волну в одном из направлений.
Рассмотрим приближенный вариант расчета разброса (разлета) кусков породы при взрыве.
Тепловая энергия Е (в единицах механической работы) взрыва ВВ массой Q:
Е=Q.q, (3.4)
где q - удельная теплота взрыва ВВ (например, для тротила q=4,2 МДж/кг).
Начальную скорость v0 разлета кусков породы находим из выражения кинетической энергии 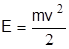 :
:
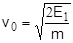 ,
,
где E1- часть энергии взрыва, приходящейся на живое сечение ω «куска» с массой m. Эта часть составляет долю сферы с поверхностью 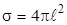 (
( 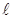 - расстояние «куска» от места взрыва):
- расстояние «куска» от места взрыва):
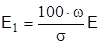 .
.
Таким образом, 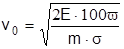 . (3.5)
. (3.5)
Исследуя баллистику (парабола) разлета «кусков» находим, что 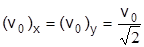 , так как самая большая дальность полета «куска», улетающего под углом 45°. Уравнение траектории полета куска породы находим из условия непрерывного перехода кинетической энергии, сообщенной телу (куску), в потенциальную. В этой задаче используется вариационный принцип - принцип Гамильтона. Этот принцип состоит в переходе из одного состояния в другое таким образом, чтобы интеграл действия (функционал) имел минимальное значение:
, так как самая большая дальность полета «куска», улетающего под углом 45°. Уравнение траектории полета куска породы находим из условия непрерывного перехода кинетической энергии, сообщенной телу (куску), в потенциальную. В этой задаче используется вариационный принцип - принцип Гамильтона. Этот принцип состоит в переходе из одного состояния в другое таким образом, чтобы интеграл действия (функционал) имел минимальное значение:
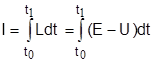 , (3.6)
, (3.6)
где Е, U - соответственно кинетическая ( 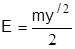 ) и потенциальная (U=mgy) энергии системы (L=Е-U - функция Лагранжа). Экстремаль y(t), дающую функционалу (3.6) минимальное значение, находим из уравнения Эйлера:
) и потенциальная (U=mgy) энергии системы (L=Е-U - функция Лагранжа). Экстремаль y(t), дающую функционалу (3.6) минимальное значение, находим из уравнения Эйлера:
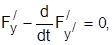
где 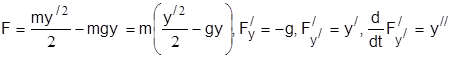 .
.
После подстановки найденных величин в уравнение Эйлера находим: у" + g = 0.
Откуда у'=-gt+с и  .
.
С учетом начальных условий (у'(t=0)=(v0)y и y(t = 0) = h) получим уравнение движения куска породы:
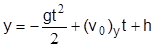 (3.7)
(3.7)
В самой высокой точке траектории у'=уy (t=t1)=0. Следовательно, из (3.7) y'=-gt+(vо)у при t=t1, имеем 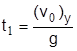 . Полное время полета куска по параболе
. Полное время полета куска по параболе 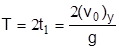 ,а радиус поражения R = (v0)x · Т.
,а радиус поражения R = (v0)x · Т.
Если рассматривается произвольный начальный угол α, то
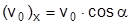 и
и 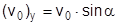 . Считаем также, что рассмотренный метод можно использовать в обратном порядке - для определения массы ВВ для известных R и m.
. Считаем также, что рассмотренный метод можно использовать в обратном порядке - для определения массы ВВ для известных R и m.
Например, для 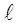 =2 м, m =4 кг, ω=0,01 м2, Q=0,6 кг находим
=2 м, m =4 кг, ω=0,01 м2, Q=0,6 кг находим 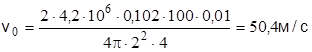 .
.
Откуда 
Полное время полета куска породы 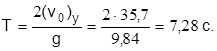
Радиус поражения R=(v0)x · T=35,7· 7,28=260м.
Приведенные примеры показывают эффективность аналитического исследования при подготовке решения.
Задачи принятия решений в условиях риска имеют место, когда каждая стратегия оперирующих сторон имеет множество исходов, каждому из которых соответствует своя вероятность его получения. В подобных задачах решение неизбежно основано на статистических характеристиках стохастических (случайных) факторов. При подготовке решения в подобных ситуациях используются два принципа: искусственное сведение стохастической задачи к детерминированной и оптимизация в среднем. В первом случае случайные факторы заменяются неслучайными величинами, что в ряде случаев может привести к значительным ошибкам. Во втором случае (оптимизация в среднем) ориентируются на получение среднего значения показателя эффективности. В большинстве случаев такой подход дает положительный результат, особенно при многократном повторении операций (см. имитационное моделирование). Этот метод не избавляет от случайности исхода, но во избежание нежелательных результатов в модель принятия решений вводят дополнительные ограничения, чтобы с заданной вероятностью вывода значение показателя эффективности было не меньше (не больше) заданного.
Гораздо сложнее вопрос стоит, когда вероятностные характеристики случайных факторов неизвестны или вообще не существуют. Для решения задач с неопределенностью разработан специальный математический раздел «Теория игр и статистических решений». Цель теории игр - выработка рекомендаций по рациональному образу действий противоборствующих сторон в конфликтной ситуации. В игре могут сталкиваться интересы двух или более сторон. Примером может служить задача выбора лучшей технологии при производстве различной продукции. Наибольшее распространение получили парные игры.
Если обозначить стратегии противоборствующих сторон
А = {А1, А2} и В = {В1, В2} , а исход применения стратегий 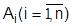 и
и 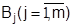 равным aij ,то игру можно представить в виде матрицы ║aij║:
равным aij ,то игру можно представить в виде матрицы ║aij║:
| В А | В1 | В2 | α |
| А1 | а11 | а12 | α1 |
| А2 | а21 | а22 | α2 |
| β | β1 | β2 |
Игры, в которых выигрыш одной стороны равен проигрышу другой называются играми с нулевой суммой. Анализ матрицы игры ║аij║ проводится на основе принципа осторожности: сторона А выбирает стратегию, при которой минимальный выигрыш максимален (принцип максимина), а сторона В свое поведение строит так, чтобы максимальный проигрыш был минимальным (минимакс). Для реализации указанного принципа анализом матрицы устанавливается нижняя цена игры.
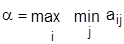 и верхняя цена игры
и верхняя цена игры 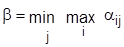 .
.
В случае α= β игра решается в чистых стратегиях (игра с седловой точкой) и обе стороны устраивает один и тот же исход аij. В случаях α ≠ β (а эти ситуации наиболее часты) игра называется игрой со смешанными стратегиями. В оптимальном варианте необходимо найти чередование нескольких стратегий Аi и Вj.
Задача анализа в этом случае - найти частоты pi, qj (вероятности) применения стратегий Аi, Bj. Оптимальные стратегии
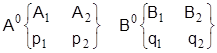
p1+p2=1 q1+q2=1 находим
из систем уравнений:  (16)
(16)
где 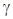 - средний гарантированный выигрыш α ≤
- средний гарантированный выигрыш α ≤ 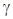 ≤ β)
≤ β)
Метод игр может быть проиллюстрирован на примере выбора наилучшего варианта сооружения или реконструкции шламохранилища.
Поскольку вышеуказанная задача многокритериальная (несколько элементов Сi системы, каждый из которых может быть выбран в качестве самостоятельного критерия безопасности) и решение принимается в условиях определённости, то для её решения можно использовать метод игр и статистических решений.
В условиях неопределённости используются критерии Лапласа, Гурвица, Сэвиджа, минимакса. Основное различие между указанными критериями определяется стратегией лица, принимающего решение в условиях большой .неопределённости. Например, критерий Лапласа, приписывающий всем возможным состояниям равные вероятности, более оптимистичен, чем принцип минимакса, рассчитывающий на лучший вариант среди худших исходов. Критерий Гурвица можно использовать при различных подходах - от наиболее оптимистичного до наиболее пессимистического. Перечисленные критерии, несмотря на их количественную природу, отражают субъективную оценку ситуации, в которой приходится принимать решение. К сожалению, не существует общих правил оценки применимости того или иного критерия, так как поведение (часто меняющееся) лица, принимающего решение, обусловленное неопределённостью ситуации, по всей видимости, является наиболее важным фактором при выборе подходящего критерия.
Все критерии, перечисленные выше, базируются на том, что лицу (группе лиц), принимающему решение, не противостоит разумный противник. Когда в роли противника выступает «природа», нет оснований предполагать, что она стремится причинить вред лицу, принимающему решение.
Данные, необходимые для принятия решений в условиях неопределённости, обычно задают в форме матрицы, строки которой соответствуют возможным действиям, а столбцы - возможным состояниям системы. Каждому действию Аi и каждому возможному состоянию Вj соответствует результат (исход), определяющий выигрыш аij (или потери rij) при выборе данного действия и реализации данного состояния.
Рассмотрим несколько вариантов принятия решений в условиях неопределённости. Сторона А, принимающая решение, имеет две стратегии:
А1 - заниженная оценка безопасности системы (это реализация принципа осторожности, пессимизма). Обычно это лучший образ действия (принцип максимина, критерий Ваальда, Сэвиджа);
А2 - завышенная оценка безопасности системы (это оптимизм при анализе факторов, влияющих на безопасность).
Сторона В характеризуется двумя состояниями :
В1 - безаварийное и В2 - аварийное. Затраты на обеспечение в поддержание безаварийного состояния или на преодоление последствий аварии изменяются в пределах от Сmin до Сmах Эти величины можно пронормировать:
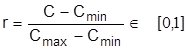 .
.
Все элементы матрицы rij можно взять в долях 1 или, после умножения всех элементов .матрицы на 10, rij ≤ 10 .
В рассмотренной ситуации матрица игры может быть записана в виде
Таблица 3.1
| B | |||
| B1 | B2 | ||
| A | A1 | r11 | r12 |
| A2 | r21 | r22 |
В таблице 3.1 можно допустить (экспертная оценка) в первом случае r22 > r21, r22 > r11, r11 < r12 < r21. В оценочных цифрах (можно рассмотреть, как это сделано ниже, различные варианты) матрица игр имеет вид:
Таблица 3.2
| B | α | |||
| B1 | B2 | |||
| A | A1 | |||
| A2 | ||||
| β |
Методы решения игр изложены в специальной литературе [19] и поэтому здесь не рассматриваются.
Находим нижнюю цену игры:
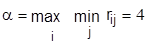
и верхнюю цену игры:
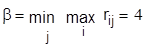
Это игра в чистых стратегиях, которая рекомендует использовать а1 (заниженную оценку безопасности) и ориентирует на безаварийную эксплуатацию объекта.
Во втором варианте принятия решений можно рассмотреть ситуацию, когда : r22 > r11 > r12> r21
Матрица игры в этом варианте имеет вид:
Таблица 3.3
| B | α | |||
| B1 | B2 | |||
| A | A1 | |||
| A2 | ||||
| β |
По данным таблицы 3.3 нижняя цена игры:
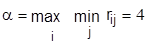
и верхняя цена игры:
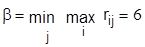
В данной ситуации α < β и , следовательно, решение может быть смешанным:
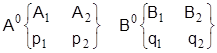
p1+p2=1 q1+q2=1
Здесь рi и qj- частоты (вероятности) использования стратегий Аi и Вj для нахождения средних потерь 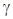 (α ≤
(α ≤ 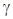 ≤ β) и pi, qj необходимо решить системы уравнений:
≤ β) и pi, qj необходимо решить системы уравнений:
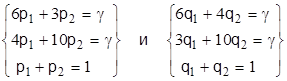
Из первой системы уравнений находим:
6р1+3(1-р1)=4р1+10(1-р1).
Откуда р1=0,78 и р2=0,22; 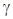 = 5,33 ( α<
= 5,33 ( α< 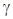 < β ) .
< β ) .
Из второй системы уравнений получим:
6q1+4(1-q1)=Зq1+10(1-q1).
Откуда q1=0,67 , q2=0,33 , 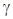 = 5,33.
= 5,33.
Таким образом, в рассмотренном случае оптимальный образ действий может быть записан как:
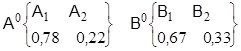
Предпочтение, хотя и не безоговорочно, и в этой ситуации отдаётся принятию решения с заниженной оценкой безопасности (р1=0,78>р2=0,22) и ориентация также в большей степени на обеспечение безаварийной эксплуатации шламохранилища (q1=:0,67>q2=0,33).
В связи с полученным анализом методом игр, влияние неопределённости при оценке безопасности шламохранилища, на наш взгляд, представляет интерес рассмотрение двух решений по шламохранилищам:
• А1 - строительство нового шламохранилища;
• А2 - реконструкция существующего шламохранилища.
Матрица игры для обоснования решения имеет вид (табл.3.1). В рассматриваемом случае а1 - решение по строительству нового шламохранилища, А2 - решение по реконструкции старого шламохранилища, В1 затраты на строительство или реконструкцию шламохранилища, В2-затраты на преодоление негативных последствий в случае возникновения аварии на шламохранилище.
Рассматриваются различные варианты соотношения затрат Сij при Аi и Вj. Также , как и в предыдущем случае, проведено нормирование Сij и все элементы rij умножены на 10. Допускается, что r22>r11 , r11>r12 , r11>r21 , r12<r21. Проанализированы различные варианты решений с отношениями
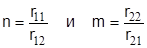
Таблица 3.4
| Варианты | |||||
| n | 1,16 | 1,14 | 1,75 | 1,8 | 2,0 |
| m | 2,5 | 2,2 | 2,0 | 1,8 | 1,5 |
Решение находилось тем же методом из принципа максимина :
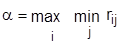 и
и 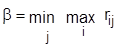
Во всех пяти вариантах имеем смешанную игру. Результаты расчётов сведены в табл. 3.5.
Таблица 3.5
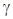 Вариант Вариант
| А | В | n | |||
| p1 | p2 | q1 | q2 | m | ||
| 0,86 | 0,14 | 0,57 | 0,43 | 6,57 | 0,464 | |
| 0,73 | 0,27 | 0,66 | 0,34 | 6,33 | 0,636 | |
| 0,625 | 0,375 | 0,75 | 0,25 | 6,25 | 0,875 | |
| 0,58 | 0,42 | 0,81 | 0,19 | 6,41 | 1,0 | |
| 0,49 | 0,51 | 0,94 | 0,06 | 6,8 | 1,33 |
Рассмотрены самые различные варианты соотношений потерь при различных вариантах сочетания Ai и Вj. Это даёт возможность проанализировать общие тенденции при обосновании решения Аi. Во-первых, во всех случаях, кроме пятого варианта, предпочтение по безопасности (риску возникновения аварии и преодоления ее. последствий) отдаётся решению по строительству нового шламохранилища. С точки зрения безопасности, это легко обосновывается (рассредоточение нагрузки, повышенная надёжность элементов сооружения, уменьшение масштабов негативного влияния экстремальных природных явлений (ураганы, бури, землетрясения). При этом учитывается высокая степень (заниженная экспертная оценка) опасности аварии и различного рода нарушений безопасности (достаточно высокое значение q2). В пятом варианте предпочтение отдаётся (с очень малым преимуществом р1=0,49 против р2=0,51) выбору решения по реконструкции старого шламохранилища. Однако, при этом следует обратить внимание, что доля влияния безопасности решения (q1=0,06) ничтожно мала по сравнению с весом затрат на реконструкцию (q1=0,94). Этот вариант имеет, на наш взгляд, не очень высокий уровень достоверности. Поэтому остаётся признать наиболее обоснованным с позиции уменьшения риска возникновения аварий на шламохранилище решение о строительстве нового сооружения.
Методы теории игр используются и в теории статистических решений. Принципиальная разница в этих задачах в том, что неопределенная ситуация не имеет конфликтной окраски. Таковы многие задачи прогнозирования разработки природных ресурсов, воздействия на окружающую среду, предсказания метеоусловий и др. Поэтому игры в теории статистических решений называются играми с природой, игрой статистика с природой или статистической игрой.
Пусть сторона А располагает стратегиями А1, А2 (в общем случае 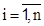 ) в условиях недостаточной информации о природе, состояния которой В1, В2,... Вm, (
) в условиях недостаточной информации о природе, состояния которой В1, В2,... Вm, ( 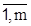 ). Исход (выигрыш или ущерб) аij (rij) заранее известен для каждой пары Аi, Вj. Кроме матрицы выигрышей (ущерба) в статистической игре могут быть известны вероятности возможных состояний природы Вj. Задача состоит в выборе оптимальной стратегии поведения стороны А. Матрица выигрышей может быть заменена на матрицу рисков
). Исход (выигрыш или ущерб) аij (rij) заранее известен для каждой пары Аi, Вj. Кроме матрицы выигрышей (ущерба) в статистической игре могут быть известны вероятности возможных состояний природы Вj. Задача состоит в выборе оптимальной стратегии поведения стороны А. Матрица выигрышей может быть заменена на матрицу рисков 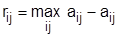
Применяются несколько критериев выбора оптимальных решений.
Согласно максиминному критерию Ваальда в качестве оптимальной выбирается стратегия Аi, при которой минимальный выигрыш по Вj максимален по Аi, то есть
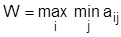
Критерий Ваальда ориентирует принимающего решение на получение максимального выигрыша в худших условиях. В связи с этим его называют критерием крайнего пессимизма.
Следующий критерий Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию, при которой величина риска принимает наименьшую величину в самой неблагоприятной обстановке, то есть: 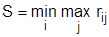
Критерий пессимизма-оптимизма Гурвица рекомендует при выборе решения в условиях неопределенности не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Он имеет вид:
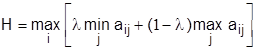 ,
,
где 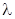 - коэффициент, выбираемый субъективно из интервала между 0 и 1. При
- коэффициент, выбираемый субъективно из интервала между 0 и 1. При 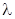 = 0 критерий Н превращается в критерий крайнего оптимизма, а при
= 0 критерий Н превращается в критерий крайнего оптимизма, а при 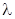 =1 - крайнего пессимизма. Задача принимающего решение - выбрать
=1 - крайнего пессимизма. Задача принимающего решение - выбрать 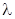 сообразно содержанию задачи. Ситуацию целесообразно анализировать с разных позиций, и если рекомендации со всех позиций совпадают, то это подтверждает правильность принимаемого решения. Если же рекомендации противоречивы, то окончательное решение следует принимать с учетом слабых и сильных сторон оптимистического и пессимистического подходов.
сообразно содержанию задачи. Ситуацию целесообразно анализировать с разных позиций, и если рекомендации со всех позиций совпадают, то это подтверждает правильность принимаемого решения. Если же рекомендации противоречивы, то окончательное решение следует принимать с учетом слабых и сильных сторон оптимистического и пессимистического подходов.
В том случае, когда неопределенность Вj характеризуется вероятностью qi , при принятии решения стремятся выбрать ту стратегию, которая дает максимум для среднего выигрыша
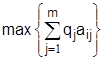
или минимум среднего риска
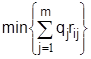
В случае, когда исход от стратегии Аi при одном и том же состоянии Вj имеет вероятностный характер, число возможных стратегий следует увеличить. Таким образом, метод статистических решений рассматривает задачи с неопределенностью и это подчеркивает важность его в задачах прогнозирования. Подробнее о методах решения игр и принятия статистических решений дано в [6].
В заключение о способах решения задач с неопределенностью отметим способ экспертных оценок. Суть метода заключается в том, что проводится анкетированный опрос компетентных лиц по интересующему вопросу (проблеме), а затем полученные ответы обрабатываются статистически. Это позволяет оценить вероятность того или иного события. Опрос может проводится в несколько этапов, становясь постепенно более конкретным. Оптимальное число экспертов - 15, а число вопросов в анкете - не более 25. Таким образом, ситуация в конечном итоге сводится к принятию решений в условиях риска. Особенно часто используется метод экспертных оценок в задачах прогнозирования.
| <== предыдущая страница | | | следующая страница ==> |
| ОБРАЗЕЦ ИСТОРИИ БОЛЕЗНИ ПО ТЕМЕ | | | Прогнозирование в горной промышленности |
Дата добавления: 2014-10-14; просмотров: 529; Нарушение авторских прав

Мы поможем в написании ваших работ!