
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Прогнозирование в горной промышленности
Временные интервалы прогнозов могут изменяться в широких пределах — от часов до многих лет в зависимости от содержания задачи. Они зависят от цикличности воздействий в системе и должны быть достаточно велики, чтобы обеспечивалась возможность нашего влияния на ожидаемые изменения. Если процесс цикличен, то прогноз составляется на период не меньший, чем продолжительность цикла. Если прогнозируемый процесс имеет тенденцию к возрастанию в течение длительного времени, то прогноз должен рассчитываться на такой промежуток времени, за который можно осуществить мероприятия но сохранению экологического равновесия окружающей среды, наращиванию мощностей и приобретению необходимого оборудования, внедрению рекомендаций по управлению процессом разработки месторождения.
Необходимость ставить на первое место сохранение равновесия в экосистеме обязывает разработчиков анализировать последствия разработки минеральных ресурсов на долговременный период. Задача очень сложная, связанная с применением решений в условиях риска и даже неопределенности из-за тесной взаимной связи всех процессов в биосфере Земли.
Генеральным направлением горнодобывающей и пере-рабатывающей отраслей должно быть создание экологически чистых технологий добычи и переработки горных пород. Совершенствование существующих производств должно быть направлено на обязательное снабжение их природоохранными сооружениями. В крайних случаях существования опасности необратимого вредного влияния производства на состояние земельных ресурсов, воздушного и водного бассейнов оно должно быть остановлено или переориентировано на новые экологически чистые технологии.
Таким образом, прогнозирование решает следующие задачи: изучение тенденций изменения потребности в тех или иных минеральных ресурсах; изучение спроса на виды продукции, предсказание новых видов изделий в будущем; оценка и распределение сырьевых баз для различных направлений использования ресурсов в народном хозяйстве; определение тенденций развития технологии и оборудования добывающе-перерабатывающих отраслей; анализ воздействий производства на экосистему, на напряженно-деформированное состояние массива; выявление перспективных направлений развития отрасли и удельного веса различных направлений использования данных полезных ископаемых в народном хозяйстве; оценка обеспеченности всеми видами ресурсов, необходимых для достижения поставленных целей; отыскание оптимальных путей достижения целей.
Основной целью объекта прогнозирования является разработка его адекватной модели, на основании которой можно было бы судить о будущих состояниях. Особенностью прогностических моделей служит невозможность прямой проверки соответствия модели и оригинала. В этом специфика и вместе с тем проблема моделирования будущего. Более распространены в прогностических моделях графические изображения (так называемые "кривые роста") и математические описания. При отсутствии теоретических предпосылок о поведении объекта исследований в будущем, используют методы аналогий и математической обработки опытных данных, характеризующих прошлое и настоящее, подбора вида и параметров формул роста, на основании которых можно прогнозировать поведение системы в будущем. Не следует забывать, что эмпирическая формула справедлива лишь для интервала опытных значений, и экстраполяция связана с погрешностью тем большей, чем дальше стремимся распространить зависимость за пределы исследованного промежутка. С целью повышения достоверности прогноза следует предусмотреть его определение несколькими различными методами. Это всегда дает хороший результат.
В основе составления и анализа прогнозов лежат различные методы: усреднение данных наблюдений в прошлом и настоящем и экстраполяция в будущее полученных зависимостей; корреляционный и регрессионный анализы; математическое программирование в задачах распределения ресурсов; имитационное моделирование с использованием метода статистических испытаний; теория игр в задачах принятия решений; анализ случайных функций; экспертные оценки и аналогии в задачах прогнозирования.
Метод усреднения наблюдений основан на допущении справедливости судить о будущем по информации о прошлом и настоящем. Процесс изменения переменной представляет собой сочетание двух составляющих - детерминированной и случайной:
y(x)=f(x)+ŋ(x)
Считается, что f(х) представляет детерминированную функцию от аргумента. Эта составляющая называется трендом, тенденцией. Подбирается f (х) в виде полинома. С повышением порядка последнего увеличивается объем необходимой информации.
Составляющая ŋ (х) считается некоррелированным случайным процессом с нулевым математическим ожиданием. Роль ŋ (х) возрастает по мере увеличения длительности прогноза или с ростом неопределенности системы. Оценка ŋ (х) в прогнозах — наиболее сложное дело. Здесь имеет место явление масштабного эффекта, под которым понимают погрешности моделирования из-за нарушения подобия (структурного, геометрического, кинематического, термического и др.) модели и объекта прогнозирования. Величина f(х) характеризует нарушение подобия во взаимодействии тел с внешней средой. Оценка случайности f(х) проводится сравнением средних значений параметров по критерию Стьюдента. Слагаемое ŋ (х) определяется вероятностной сущностью структуры горных пород, процессов переноса вещества, импульса и энергии. Оценка неслучайности ŋ (х) проводится сравнением дисперсий величин по критерию Фишера.
Чем шире теоретическая информация о существе прогнозируемых процессов, тем с большим основанием можно экстраполировать эмпирическую формулу. Положительный результат достигается при сочетании, комбинировании различных методов прогнозирования. Решению задач прогнозирования может помочь использование подобия общих закономерностей напряженно-деформированного состояния горных пород, роста характеристик технических устройств, биологического и социального развития.
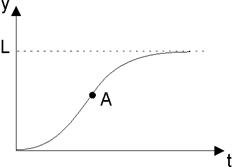 Среди "кривых роста" в прогнозах особое место занимает S-образная кривая Перла (рис.3.1), которой подчиняется изменение эффективности тепловых электростанций, кпд паровых двигателей в течение всего периода их развития.
Среди "кривых роста" в прогнозах особое место занимает S-образная кривая Перла (рис.3.1), которой подчиняется изменение эффективности тепловых электростанций, кпд паровых двигателей в течение всего периода их развития.
 Этой кривой соответствует тенденция роста объема производства минеральных удобрений в мире. Заметна тенденция приближения объема этого производства к пределу — асимптоте. Особенность кривой Перла состоит в ее получении из допущения пропорциональности скорости изменения функции текущему значению и расстоянию до асимптоты (возможного предела изменения функции). Кривая Перла позволяет предсказать скорость, с которой новое технологическое решение вытесняет предыдущее, устаревшее, используемое для получения той же продукции. В других случаях нас интересует скорость адаптации новой техники, так как естественно вначале недоверие к ней, внедрение новых идей идет трудно, и лишь постепенно темп растет. Со временем возможности существующей технологии исчерпываются, что характеризуется уменьшением скорости роста. На кривых Перла этот момент характеризуется точкой перегиба (точка А на рис.3.1). В подобных ситуациях возникает необходимость замещения старой техники, технологии новыми, основанными на революционных идеях и решениях. Многие исследователи считают, что замещение одной (старой) технологии другой (новой) представляется S-образными кривыми роста (Перла, Гомперца). Например, замена паруса двигателем, дерева — металлом в судостроении характеризуется S-образной кривой. Используя кривые роста, можно прогнозировать темпы увеличения характеристик, определить "потолок", а при известном пределе можно предсказывать темп роста функциональных характеристик в будущий период. Одной из важнейших проблем прогнозирования служит предсказание тенденций роста за пределами существующей технологии с учетом неизвестных в настоящее время новых видов продукции.
Этой кривой соответствует тенденция роста объема производства минеральных удобрений в мире. Заметна тенденция приближения объема этого производства к пределу — асимптоте. Особенность кривой Перла состоит в ее получении из допущения пропорциональности скорости изменения функции текущему значению и расстоянию до асимптоты (возможного предела изменения функции). Кривая Перла позволяет предсказать скорость, с которой новое технологическое решение вытесняет предыдущее, устаревшее, используемое для получения той же продукции. В других случаях нас интересует скорость адаптации новой техники, так как естественно вначале недоверие к ней, внедрение новых идей идет трудно, и лишь постепенно темп растет. Со временем возможности существующей технологии исчерпываются, что характеризуется уменьшением скорости роста. На кривых Перла этот момент характеризуется точкой перегиба (точка А на рис.3.1). В подобных ситуациях возникает необходимость замещения старой техники, технологии новыми, основанными на революционных идеях и решениях. Многие исследователи считают, что замещение одной (старой) технологии другой (новой) представляется S-образными кривыми роста (Перла, Гомперца). Например, замена паруса двигателем, дерева — металлом в судостроении характеризуется S-образной кривой. Используя кривые роста, можно прогнозировать темпы увеличения характеристик, определить "потолок", а при известном пределе можно предсказывать темп роста функциональных характеристик в будущий период. Одной из важнейших проблем прогнозирования служит предсказание тенденций роста за пределами существующей технологии с учетом неизвестных в настоящее время новых видов продукции.
Применимость для данной задачи кривой Перла 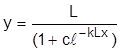 проще определить приведением этой зависимости к линейному виду заменой
проще определить приведением этой зависимости к линейному виду заменой 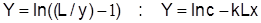
Исследованием графической зависимости Y(х) визуально или с помощью коэффициента корреляции убеждаемся в правомерности использования кривой Перла в данном случае.
Следует отметить характерную ошибку в прогнозах, когда на основании постоянной скорости роста в прошлом предполагают ту же скорость процесса в будущем. Такой подход в прогнозировании называется "наивным" в том смысле, что все происходящее в прошлом и сформировавшаяся тенденция в настоящем будут иметь место и в будущем. В двух случаях "наивная экстраполяция" неприменима - при наличии естественного предела (истощение ресурса и др.) и при изменении факторов, обуславливающих тенденцию в прошлом (темпы осушения, воздействие на окружающую среду и др.). Достаточно часто в прогнозах используют экспоненциальный рост, вызванный бурным развитием техники и технологии. Экстраполяция процесса в будущее в виде экспоненциальной функции в ряде случаев дает заведомо неверный результат.
Повысить достоверность модели прогноза можно, если учесть теоретические представления об изучаемом процессе. Это позволяет ограничиться минимумом экспериментальных данных и дает возможность обоснованной экстраполяции за пределами проведенных исследований. В некоторых случаях удается воспользоваться известными заранее соотношениями для скорости процессов (деформирования, нагревания, охлаждения, фильтрации и др.) или данными об угловом коэффициенте касательной к искомой траектории.
Таким образом, степень достоверности прогностической модели зависит от умения рассматривать ситуацию с различных точек зрения при сочетании различных методов решения задачи.
§3.3.Методы оптимизации.
Математическая модель, предназначенная для подготовки и обоснования наилучшего решения, содержит функцию цели и дополнительные условия – ограничения в виде уравнений. Критерий оптимизации, зависимость которого от искомых и заданных параметров представляет функцию цели, должен иметь количественную оценку, как правило, изменяющуюся монотонно. Объект оптимизации должен располагать определенными степенями свободы, то есть управляющими воздействиями, за счет которых можно менять его состояние. Главная проблема решения многокритериальных задач: - сведение их к однокритериальным, так как в принципе нельзя одновременно достичь экстремума нескольких несовместимых критериев (например, максимум производительности при одновременном наилучшем качестве и минимальных затратах и т.д.). В этом случае применяют обобщенный критерий – функцию желательности, метод Паретовских решений, метод последовательных уступок и другие.
Оптимизация предполагает использование различных математических методов поиска наилучшего решения.
Наиболее часто, если функция цели представлена аналитической непрерывной зависимостью, применяется метод исследования функций на экстремум (определяется первая производная и приравнивается нулю, а затем знак производной исследуется в области экстремума). В случае, если в задаче необходимо определить экстремум функции Z(x,y) при наличии ограничений типа f(x,y), применяют метод Лагранжа. Вводится в рассмотрение функция 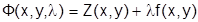 , где
, где 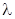 - множитель Лагранжа.
- множитель Лагранжа.
Координаты оптимальной точки 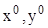 и параметр
и параметр 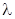 находятся из системы уравнений:
находятся из системы уравнений:
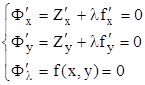
Характер экстремума определяется соотношениями:
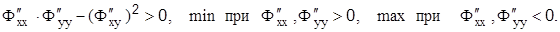
Метод множителей Лагранжа может быть использован при определении оптимальной формы и размеров различных геометрических объектов (бункеров, гранул, отвалов, профилей различных сооружений и т.д.), при распределении сырья, продукции между параллельно работающими конвейерами и в других задачах.
Вариационное исчисление применяется во многих задачах механики. Например, при определении моментов инерции, центра тяжести, уравнения траектории, поверхности, площади поверхности вращения и других. Многие задачи механики и физики в целом сводятся к утверждению, что функционал в рассматриваемом процессе должен достигать максимума или минимума. Эти законы носят название вариационных принципов механики. К числу вариационных принципов принадлежат: принцип наименьшего действия, законы сохранения энергии, импульса, принцип Кастилиано в теории упругости и другие.
Таким образом, многие инженерные задачи связаны с необходимостью поиска функции y(x), реализующей экстремум (max или min)функционала 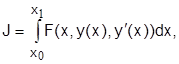 где
где 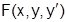 - заданное выражение.
- заданное выражение.
Необходимым условием существования экстремума функционала J служит уравнение Эйлера 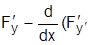 )=0. Экстремаль y(x), найденная из уравнения Эйлера, должна удовлетворять граничным условиям. Характер экстремума определяется по знаку второй производной F по
)=0. Экстремаль y(x), найденная из уравнения Эйлера, должна удовлетворять граничным условиям. Характер экстремума определяется по знаку второй производной F по 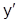 (условие Лежандра): при
(условие Лежандра): при 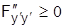 имеем minJ, а при
имеем minJ, а при 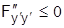 - maxJ.
- maxJ.
Если функция в подынтегральном выражении содержит производные более высокого порядка 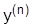 :
:
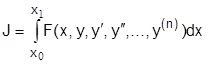
с граничными условиями
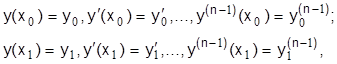
то уравнение Эйлера принимает вид:
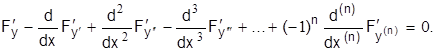
А в тех случаях, когда требуется найти систему функций 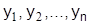 , реализующую экстремум функционала
, реализующую экстремум функционала
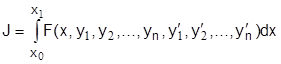
совместно с условиями вида 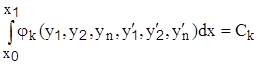
(Ск- заданные постоянные), для гладких функций 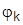 применим метод Лагранжа:
применим метод Лагранжа:
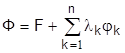 .
.
И в этом случае неизвестные функции 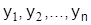 и множители Лагранжа
и множители Лагранжа 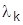 находятся из системы уравнений Эйлера, решенных совместно с дополнительными условиями в виде интегралов.
находятся из системы уравнений Эйлера, решенных совместно с дополнительными условиями в виде интегралов.
Метод линейного программирования особенно эффективен в геолого-экономических задачах оптимального выбора, распределения и использования сырьевых, материальных и других видов ресурсов. Среди решенных задач линейного программирования можно указать задачи составления смесей, шихты, распределения площадей под разработку, календарное планирование, транспортные задачи снабжения n- потребителей продукции (сырья) с m-предприятий при условии минимальных транспортных и других видов издержек.
Модель линейного программирования состоит из совокупности линейных уравнений и неравенств, выражающих функцию цели и ограничения на нее. Математическая модель линейного программирования имеет вид:
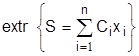 (3.8)
(3.8)
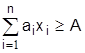 (3.9)
(3.9)
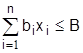 (3.10)
(3.10)
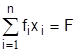 (3.11)
(3.11)
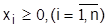
В задачах на min (3.8) преобладают ограничения типа (3.9), на max – типа (3.10), в транспортных задачах nxm – (3.11). Критерий оптимизации S (3.8) чаще всего является экономическим (прибыль, приведенные затраты, рентабельность), но применяются и технологические показатели (производительность, часы работы, площади и объемы разработок и т.д.). Ограничения (3.9)-(3.11) представляют собой ограничения по материальным, сырьевым, трудовым ресурсам, мощностям, соотношения технологий и многое другое.
Большинство практически значимых задач линейного программирования связано с поиском большого числа неизвестных (от десятков до тысяч) и поэтому требует для своего решения применения вычислительной техники. Многие типовые задачи имеют стандартное обеспечение.
Однако не следует забывать, что при сравнительно небольшом числе неизвестных (например, до 10) может с успехом применяться ручной способ решения симплекс-методом, а в случае двух неизвестных (выбор оптимального варианта из двух существующих) эффективно используется наглядный геометрический метод решения. С этой целью с помощью уравнений-ограничений строим область Д допустимых решений. Оптимальное решение (точка или множество точек) находится в одной из вершин или во множестве точек одной из сторон области Д. Для заданного (любого) значения S строится функция цели и затем мысленно перемещается от начала координат в сторону области Д. Первая точка области Д, которой касается функция цели, точка минимума, а последняя точка области Д, которой касается 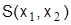 при выходе из Д, дает координаты
при выходе из Д, дает координаты 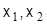 максимума.
максимума.
Для более подробного ознакомления с особенностями линейного программирования авторы отсылают читателя к специальной литературе [5,16].
Динамическое программирование (планирование) применяется для нахождения оптимальных решений в многошаговых (многоэтапных) задачах. Принцип оптимальности динамического программирования сформулирован впервые Р.Беллманом: «Оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, полученного в результате первоначального решения.»
Примерами задач, решаемых методом динамического программирования, могут служить:
- планирование производственной программы по периодам года при минимальных затратах на производство и содержание запасов;
- оптимальное распределение средств и ресурсов на расширение производства при максимизации прироста выпуска продукции;
- оптимальное планирование замены устаревшего оборудования более совершенным при максимизации прибыли;
- календарное планирование ремонта либо замены устаревшего оборудования при минимуме эксплуатационных затрат;
- выбор оптимального маршрута при минимуме транспортных расходов и т.д.
Любую многоэтапную задачу можно решать двумя способами: искать оптимальное решение сразу на всем протяжении процесса или строить его шаг за шагом. После оптимизации i-го шага, исходя из результатов предыдущего, оптимизируют следующий (i+1)-й шаг. Второй способ проще и, конечно, эффективнее. Его суть в постепенной, поэтапной оптимизации, что особенно ценно в задачах, в которых ситуация меняется во времени и пространстве и поэтому необходимо планировать события с учетом изменяющихся факторов.
Принцип оптимальности Беллмана реализуется в виде рекуррентного соотношения:
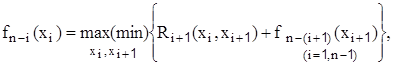
где 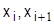 - решение (управление), выбранное на i-том шаге (дуга из xi в xi+1);
- решение (управление), выбранное на i-том шаге (дуга из xi в xi+1); 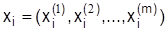 - состояние системы на i-то шаге; Ri – эффект, достигнутый на i-том шаге; fn-i – оптимальное значение эффекта, достигаемого за n-i – шагов; n-число шагов (этапов).
- состояние системы на i-то шаге; Ri – эффект, достигнутый на i-том шаге; fn-i – оптимальное значение эффекта, достигаемого за n-i – шагов; n-число шагов (этапов).
Указанная формула в словесной форме может быть записана так:
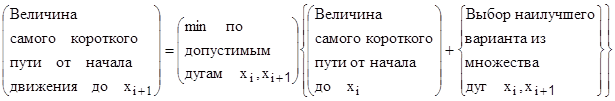
Чтобы определить оптимальное решение по указанной рекуррентной формуле необходимо выполнить следующее (например, в задаче на max):
1. Записать функциональное уравнение для последнего состояния процесса, системы (для i=n-1):
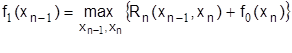
2. Найти 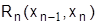 из дискретного набора его значений при некоторых фиксированных
из дискретного набора его значений при некоторых фиксированных 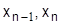 (так как всегда начальное условие принимают
(так как всегда начальное условие принимают 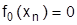 , то
, то 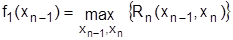 .
.
В результате первого шага известно решение 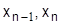 и значение
и значение 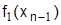 .
.
3. Уменьшить значение i на единицу и записать соответствующую рекуррентную формулу для второго шага.
4. Найти условно-оптимальное решение на втором шаге (этапе).
5. При i=0 расчет условно-оптимальных значений заканчивается, так как найдено оптимальное решение для первого состояния системы.
6. Вычислить оптимальное решение задачи для каждого последующего шага процесса, двигаясь от конца маршрута к началу.
Задачи оптимизации с нелинейными или трудно вычислимыми соотношениями являются предметом нелинейного программирования.
Как правило, решения задач нелинейного программирования могут быть найдены лишь численными методами с применением вычислительной техники. Среди них наиболее часто пользуются градиентными методами (методы релаксации, градиента, наискорейшего спуска и восхождения), а также безградиентными методами детерминированного поиска (методы сканирования, симплексный и другие) и методами случайного поиска.
§3.4.Элементы теории вероятностей и математической
статистики.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение. Случайные величины могут быть дискретными (фиксированными) или непрерывными, принимающими любое значение в заданном интервале.
Вероятность события – это численная мера объективной возможности этого события. Она изменяется от нуля (невозможность события) до 1 (достоверное событие). Если ввести понятие относительной частоты (частости) события, как отношение числа случаев ni, благоприятствующих событию i, ко всем наблюдавшимся случаям (n), то вероятность i-го события находится по формуле 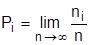 .
.
Сумма вероятностей всех возможных событий i равна 1, т.е. 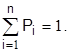 При достаточно большом значении n относительная частота достаточно правильно отражает (оценивает) значение вероятности события. Суммарная вероятность (
При достаточно большом значении n относительная частота достаточно правильно отражает (оценивает) значение вероятности события. Суммарная вероятность ( 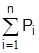 ) распределена определенным образом между отдельными i-ми событиями. Случайная величина полностью задана, если известно ее распределение. Закономраспределения называется соотношение между возможными значениями случайной величины и соответствующими им вероятностями.
) распределена определенным образом между отдельными i-ми событиями. Случайная величина полностью задана, если известно ее распределение. Закономраспределения называется соотношение между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой задания закона распределения дискретной случайной величины служит таблица, в которой перечислены все значения xi и pi
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
 Указанная таблица называется рядом распределения.
Указанная таблица называется рядом распределения.
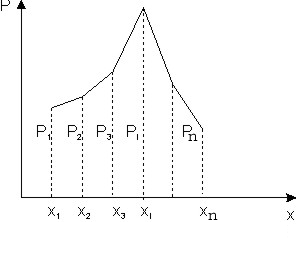
Для наглядности ряд распределения часто изо-бражается графически. Для этого по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – вероятности этих зна-чений. Полученная гео-метрическая фигура (рис.3.2.) называется мно-гоугольником (полигоном) распределения.
Иногда удобна «механическая» интерпретация ряда распределения. Это некоторая масса, равная 1 и распределенная по оси х так, что в отдельных точках x1,x2,…,xn помещены соответствующие массы P1,P2,…,Pn.
Для количественной характеристики распределения непрерывной случайной величины удобно пользоваться не вероятностью данного события Х=х, а вероятностью события Х<х, где х - текущая переменная. Вероятность события Х<х величина переменная функция от х. Эта функция называется функцией распределения случайной величины Х и обозначается F(x): F(x)=P(X<x).
Функцию распределения называют иногда интегральной функцией распределения или интегральным законом распре-деления. Она обладает свойствами:
а) F(x) – неубывающая функция своего аргумента, т.е. при х2>x1
F(х2)>F(x1);
б) На минус бесконечности F(x) равна нулю ( 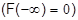 );
);
в) На плюс бесконечности F(x) равна 1 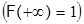 ;
;
График F(x) в общем виде показаны на рис.3.3.
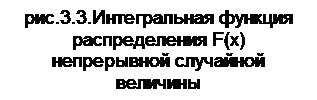
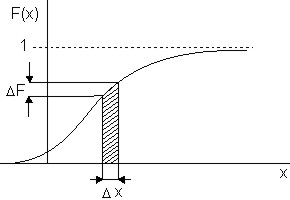 Если для непрерывных случайных величин F(x) сплошная гладкая линия, то для дискретных величин F(x) выражается ступенчатой линией, скачки которой наблюдаются в точках возможных значений случайных величин и соответствующих им вероятностей.
Если для непрерывных случайных величин F(x) сплошная гладкая линия, то для дискретных величин F(x) выражается ступенчатой линией, скачки которой наблюдаются в точках возможных значений случайных величин и соответствующих им вероятностей.
Сумма высот всех скачков равна 1. По мере увеличения числа возможных значений случайной величины скачки становятся меньше по высоте и функция F(x) все ближе приближается к распределению непрерывной величины. В пределе при 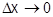 закон распределения дискретной величины приближается к функции распределения непрерывной величины. Вероятность попадания случайной величины на заданный участок
закон распределения дискретной величины приближается к функции распределения непрерывной величины. Вероятность попадания случайной величины на заданный участок 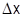 равна приращению функции распределения на этом участке. Вероятность любого отдельного значения непрерывной случайной величины равна нулю. Вычисляя вероятность попадания в интервал
равна приращению функции распределения на этом участке. Вероятность любого отдельного значения непрерывной случайной величины равна нулю. Вычисляя вероятность попадания в интервал 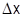 , воспользуемся понятием производной. Тогда
, воспользуемся понятием производной. Тогда
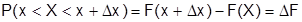
Или в пределе 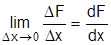 . Обозначим
. Обозначим 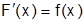 . Производная функции распределения f(x) называется плотностью распределения (характеризует плотность распределения случайной величины). Плотность распределения иногда называют дифференциальной функцией распределения. Это одна из форм закона распределения. Эта функция существует только для непрерывных случайных величин (условие дифференцируемости). Вероятность попадания в элементарный промежуток
. Производная функции распределения f(x) называется плотностью распределения (характеризует плотность распределения случайной величины). Плотность распределения иногда называют дифференциальной функцией распределения. Это одна из форм закона распределения. Эта функция существует только для непрерывных случайных величин (условие дифференцируемости). Вероятность попадания в элементарный промежуток 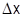 равна вероятности
равна вероятности 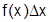 . Вероятность попадания на отрезок
. Вероятность попадания на отрезок 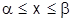 равна:
равна:
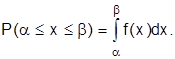
Геометрически это площадь криволинейной трапеции в промежутке 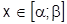 .
.
Связь функции распределения с плотностью распределения дается формулой:
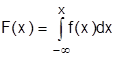 .
.
Свойства плотности распределения:
а) Плотность распределения неотрицательная функция: 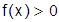 .
.
б) Интеграл в бесконечных пределах от плотности вероятности равен 1, т.е. 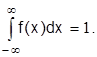
Размерность: F(x) – безразмерная; f(x) - имеет размерность, обратную случайной величине.
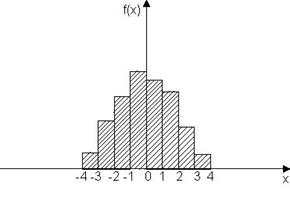 Гистограмма – это статистический ряд, оформленный графически. Для построения гистограммы на оси абсцисс откладываются интервалы и на каждом из интервалов, как на основании, строится прямоугольник, площадь которого равна относительной частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника (рис.3.4.).
Гистограмма – это статистический ряд, оформленный графически. Для построения гистограммы на оси абсцисс откладываются интервалы и на каждом из интервалов, как на основании, строится прямоугольник, площадь которого равна относительной частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника (рис.3.4.).
Этот график представляет собой плотность распределения случайной величины Х. Интервалы для построения гистограмм выбираются произвольно, но для определения оптимальной величины интервала можно применять формулу:
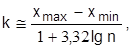
где 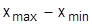 - размах изменения случайной величины; n –число наблюдений в выборке.
- размах изменения случайной величины; n –число наблюдений в выборке.
В качестве основных числовых характеристик применяется математическое ожидание, дисперсия, асимметрия, эксцесс.
Математическим ожиданием случайной величины называется сумма произведений значений случайной величины на вероятность этих значений: 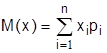 (при достаточно больших n математическое ожидание может быть оценено средним арифметическим
(при достаточно больших n математическое ожидание может быть оценено средним арифметическим 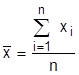 ).
).
Для непрерывной случайной величины:
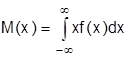
Свойства математического ожидания:
а) 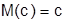
б) 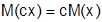
в) 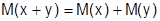
г) 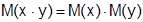
Дисперсией (рассеиванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
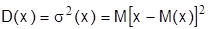
Для дискретных величин:
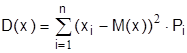
И для непрерывных случайных величин:
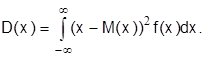
Свойства дисперсии:
а) 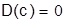
б) 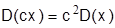
в) 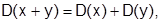 если x и y независимы.
если x и y независимы.
г) 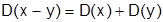
д) 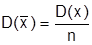 (Отсюда свойство стандартного отклонения
(Отсюда свойство стандартного отклонения 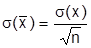 ).
).
е) 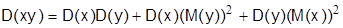 , если x и y независимы.
, если x и y независимы.
Размерность D(x) равна квадрату размерности случайной величины.
Мода случайной величины (М0) – это ее наиболее вероятное значение. В общем случае M(x) и М0 не совпадают, но при симметричном (нормальном) распределении оказывается М0= M(x).
Медианой случайной величины (Ме) называется ее данное значение, для которого 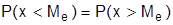 . Медиана делит площадь, ограниченную плотностью распределения
. Медиана делит площадь, ограниченную плотностью распределения 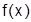 пополам.
пополам.
Асимметрия – характеристика, служащая для определения степени скошенности плотности распределения. Для симметричного распределения 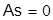 . Для выборочной совокупности наблюдений
. Для выборочной совокупности наблюдений
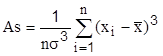 ,
,
Для дискретных случайных величин
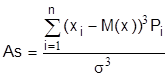 ,
,
а для непрерывных
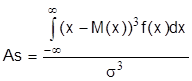 .
.
Эксцесс служит для характеристики крутости плотности распределения
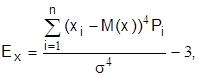
если рассматриваются дискретные величины, а для непрерывных
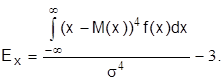
При 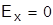 имеет место нормальное распределение (распределение Гаусса). Для выборочной совокупности наблюдений
имеет место нормальное распределение (распределение Гаусса). Для выборочной совокупности наблюдений
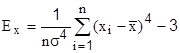 .
.
Обычно характеристики 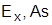 применяют при
применяют при 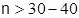 . Отличные от нуля
. Отличные от нуля 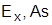 указывают на отклонение распределения от нормального.
указывают на отклонение распределения от нормального.
Нормальным называют распределение вероятностей непрерывной случайной величины, которая описывается дифференциальной функцией
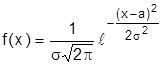
Кривая распределения по нормальному закону симметрична, имеет холмообразный (колоколообразный) вид (рис.3.5.). Определяется двумя параметрами:
|
 математическим ожиданием и средним квадратическим отклонением. Математическое ожидание нормального распределения равно
математическим ожиданием и средним квадратическим отклонением. Математическое ожидание нормального распределения равно 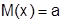 , а среднеквадратическое отклонение нормального распределе-ния равно
, а среднеквадратическое отклонение нормального распределе-ния равно 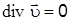 и
и 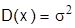 . Максимальная ордината кривой равна
. Максимальная ордината кривой равна 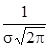 , соответствует мате-
, соответствует мате-
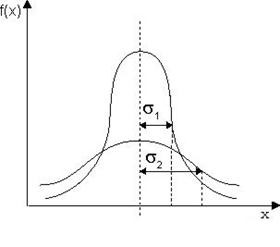
матическому ожиданию. Точка перегиба соответствует величине среднеквадратического отклонения 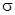 . Плотность распределения f(x) при
. Плотность распределения f(x) при 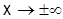 стремится к f(x)=0. Наибольшая ордината обратно пропорциональна
стремится к f(x)=0. Наибольшая ордината обратно пропорциональна 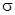 . С увеличением
. С увеличением 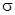 вершина f(x) опускается, а сама кривая становится более плоской (рис. 3.5.).
вершина f(x) опускается, а сама кривая становится более плоской (рис. 3.5.).
Нормированным называют нормальное распределение с параметрами a=0 и 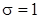 . Нормирование проводят введением параметра
. Нормирование проводят введением параметра 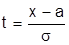 . В этом случае M(t)=0, а
. В этом случае M(t)=0, а 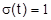 . Дифференциальная функция нормированного распределения:
. Дифференциальная функция нормированного распределения:
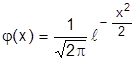
Эта функция табулирована. Вероятность того, что Х примет значение, принадлежащее интервалу 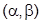 , равна
, равна
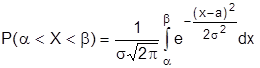 .
.
Обозначив 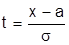 , преобразуем интеграл в виде функции Лапласа
, преобразуем интеграл в виде функции Лапласа 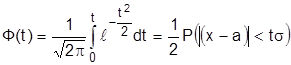 .
.
Функция Ф(t) называется интегралом вероятности, ее значения можно найти в справочных таблицах. Р – вероятность попадания случайной ошибки в симметричный интервал 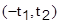 . В таблицах значения Ф(t) даны лишь для положительных t, а для отрицательных значений аргумента справедливо выражение:
. В таблицах значения Ф(t) даны лишь для положительных t, а для отрицательных значений аргумента справедливо выражение:
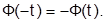
Вероятность попадания в любой интервал 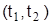 в случае нормального закона:
в случае нормального закона: 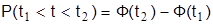 .
.
И, наконец, вероятность того, что случайная ошибка выйдет за границы 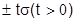 равна:
равна: 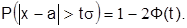
При больших значениях t вероятность Р очень мала. Так, при 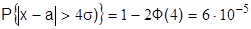 ,
, 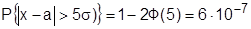 . Вероятность выхода за пределы
. Вероятность выхода за пределы 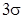 уже настолько мала, что ее считают невозможной. Отсюда следует правило трех сигм: случайные ошибки измерения практически ограничены по абсолютной величине значением
уже настолько мала, что ее считают невозможной. Отсюда следует правило трех сигм: случайные ошибки измерения практически ограничены по абсолютной величине значением 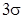 .
.
Для анализа близости экспериментального распределения нормальному закону используют критерий согласия 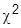 («
(« 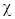 и» – квадрат):
и» – квадрат):
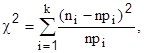
который при достаточно большом числе испытаний n приближенно распределен по закону 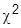 с (к-3) степенями свободы. В формуле pi – оценка вероятности попадания в интервал
с (к-3) степенями свободы. В формуле pi – оценка вероятности попадания в интервал 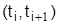 , находится как разность значений функции Лапласа:
, находится как разность значений функции Лапласа:
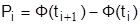 .
.
Найденное значение 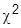 сравнивается с табличными значениями. По числу степеней свободы
сравнивается с табличными значениями. По числу степеней свободы 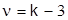 и экспериментальному
и экспериментальному 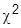 находим вероятность Р того, что рассматриваемое различие экспериментального и нормального распределений является случайным. Малые значения Р соответствуют малой вероятности случайного отличия и свидетельствуют о наличии систематических отклонений от нормального закона. Нормальный закон распределения случайной величины имеет место, когда исходы их представляют собой сумму большого числа независимых величин, дисперсии которых малы по сравнению с дисперсией всей суммы.
находим вероятность Р того, что рассматриваемое различие экспериментального и нормального распределений является случайным. Малые значения Р соответствуют малой вероятности случайного отличия и свидетельствуют о наличии систематических отклонений от нормального закона. Нормальный закон распределения случайной величины имеет место, когда исходы их представляют собой сумму большого числа независимых величин, дисперсии которых малы по сравнению с дисперсией всей суммы.
В том случае, если возможные значения случайной величины лежат в интервале (а,b) и нет оснований отдать предпочтение какому-либо из этих значений, то имеет место закон равномерной плотности распределения. Этому закону может подчиняться, например, погрешность при измерениях, если ни одному из возможных значений нельзя отдать предпочтение.
Закон равномерного распределения записывается в виде (рис. 3.6.)
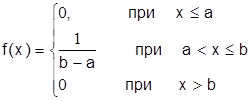
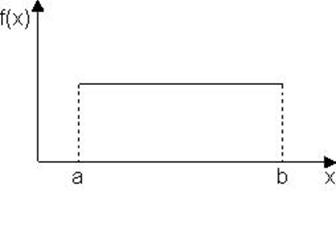 Математическое ожидание в этом случае
Математическое ожидание в этом случае 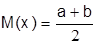 и средне-квадратическое отклонение
и средне-квадратическое отклонение
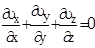
|
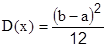 )
)
Медиана совпадает с математическим ожиданием, а моды этот закон не имеет, так как все значения плотности вероятности равны между собой.
Показательным (экспоненциальным) называют распре-деление вероятностей, которое описывается дифференциальной функцией
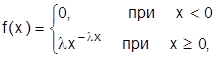
где 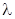 - постоянная положительная величина. Как видим, показательный закон распределения определяется всего одним параметром
- постоянная положительная величина. Как видим, показательный закон распределения определяется всего одним параметром 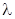 . Эта особенность указывает на преимущество этого закона распределения. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий в потоке. Интегральная функция показательного закона распределения:
. Эта особенность указывает на преимущество этого закона распределения. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий в потоке. Интегральная функция показательного закона распределения:
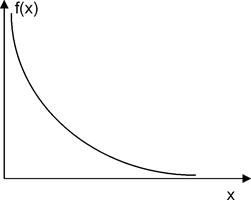
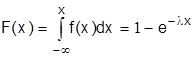 .
.
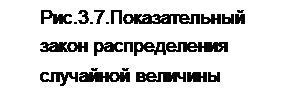 График показательного закона распределения показан на рис. 3.7. Вероятность попадания в интервал (a,b) непрерывной случайной величины, распределенной по показательному закону, находится по формуле
График показательного закона распределения показан на рис. 3.7. Вероятность попадания в интервал (a,b) непрерывной случайной величины, распределенной по показательному закону, находится по формуле
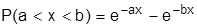
Математическое ожидание показательного распределения равно обратной величине параметра 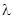 :
:
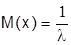 .
.
Дисперсия распределения в этом случае 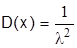 , а среднее квадратическое отклонение
, а среднее квадратическое отклонение 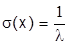 . Следовательно, в случае показательного закона распределения
. Следовательно, в случае показательного закона распределения 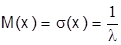 .
.
Показательное распределение широко применяется в приложениях, в частности, в теории надежности.
Часто длительность времени безотказной работы элемента имеет показательное распределение, интегральная функция которого
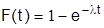 .
.
Функция надежности, определяющая вероятность безотказной работы элемента за время длительностью t, в случае показательного распределения времени безотказной работы элемента имеет вид:
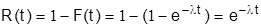 .
.
Таким образом, показательным законом надежности называют функцию надежности
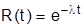 ,
,
где 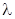 - интенсивность отказов (среднее число событий в единицу времени). Если на практике изучается показательное распределение с неизвестным параметром
- интенсивность отказов (среднее число событий в единицу времени). Если на практике изучается показательное распределение с неизвестным параметром 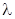 , то при отсутствии данных о значении математического ожидания используют его приближенную оценку – арифметическое среднее, т.е.
, то при отсутствии данных о значении математического ожидания используют его приближенную оценку – арифметическое среднее, т.е. 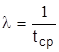 .
.
Для оценки справедливости гипотезы о показательном распределении находят выборочную среднюю 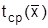 и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение 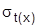 . Если эти величины
. Если эти величины 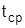 и
и 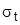 отличаются незначительно, то есть все основания считать справедливым применение экспоненциального закона распределения случайных величин. В противном случае от этой гипотезы следует отказаться.
отличаются незначительно, то есть все основания считать справедливым применение экспоненциального закона распределения случайных величин. В противном случае от этой гипотезы следует отказаться.
Нередко возникает необходимость сравнения результатов экспериментов различных серий с целью установления закономерного или случайного характера расхождения. Например, одна и та же характеристика измеряется разными приборами или способами (типовым или экспериментальным) или сравниваются свойства одной и той же горной породы, но пробы которой взяты из разных месторождений. В результате сравнения средних и дисперсий устанавливают, является ли расхождение случайным или нет с заданной надежностью вывода. Если расхождение не случайно, то следует искать причину этого (различие состава породы из разных месторождений, ошибка выбранного принципа измерения и т.д.). Если же расхождения случайны, то измерения двух серий наблюдений могут быть объединены в одну совокупность. Таким образом, это также вопрос сопоставимости результатов исследований различных авторов или сравнения качества изделий с одними и теми же номинальными характеристиками, но изготовленными на разном оборудовании или по различным технологиям.
Сравнение средних значений проводится следующим образом. Пусть с одной и той же точностью произведены две серии независимых измерений и при этом n1 наблюдений первой серии дали средние значения 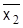 , и эмпирическую дисперсию σ12, а во второй серии соответственно получили n2,
, и эмпирическую дисперсию σ12, а во второй серии соответственно получили n2, 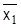 , σ22 . Напомним, что
, σ22 . Напомним, что
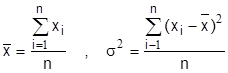
для большой выборки (п>30) и
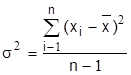
для малой выборки (п<30).
Для решения вопроса о случайном или неслучайном расхождении средних значений рассчитываем отношение
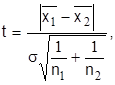 3.12)
3.12)
где
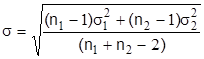 (3.13)
(3.13)
Задаем желаемую вероятность вывода Р и по табл. 3.6 находим значение t(P,f), соответствующее заданной вероятности Р и числу степеней свободы f=n1+n2-2.
Таблица 3.6
Значения распределения t(Р, f) Стьюдента
| f | ||||||||||||
| Р | 0,9 | 2,132 | 2,015 | 1,943 | 1,895 | 1,860 | 1,833 | 1,812 | 1,734 | 1,725 | 1,676 | 1,660 |
| 0,95 | 2,776 | 2,571 | 2,447 | 2,365 | 2,306 | 2,262 | 2,228 | 2,103 | 2,086 | 2,008 | 1,984 | |
| 0,99 | 4,604 | 4,032 | 3,707 | 3,499 | 3,355 | 3,250 | 3,169 | 2,878 | 2,845 | 2,677 | 2,626 |
Если абсолютная величина расчетного значения t по (3.12) превосходит найденное табличное значение t(Р,f), то расхождение средних значений можно считать неслучайным (значимым) с надежностью вывода Р. В противном случае нет оснований считать расхождение значимым. При значимом расхождении следует выяснить причины этого и сделать выводы о степени пригодности нового метода или прибора, технологии.
Заметим, что если расчетное отношение t оказывается немногим меньше значения t(Р, f) при заданном Р, то может быть целесообразным увеличить число измерений для получения более надежного вывода, тем более, что значения t(Р, f) уменьшаются с увеличением f.
Сравнение точности различных измерительных приборов, степени влияния случайных факторов и многие другие исследовательские и производственные задачи связаны с анализом дисперсий различных серий наблюдений.
Для решения вопроса о случайном или неслучайном расхождении дисперсий рассматривают отношение большей эмпирической дисперсии к меньшей (критерий Фишера):
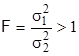 (3.14)
(3.14)
Затем задают желаемую надежность вывода Р и находят по известным степеням свободы f1=n1-1 и f2=n2-1 критическое значение отношения F (табл. 3.7).
Если отношение F по (3.14) оказывается больше критического (табличного) значения Fкр, то расхождение дисперсий считается неслучайным (значимым) с надежностью вывода Р. В этом случае следует искать причину неслучайного расхождения. В противном случае для этого нет оснований.
Таблица 3.7.
Критические значения отношения Fкр по формуле (3.14)
для Р=0.95.
| f2 | f1 | ||||||
| 4,53 | 4,28 | 4,15 | 4,06 | 3,94 | 3,87 | 3,81 | |
| 4,12 | 3,87 | 3,73 | 3,63 | 3,50 | 3,44 | 3,38 | |
| 3,84 | 3,58 | 4,44 | 3,34 | 3,21 | 3,15 | 3,08 | |
| 3,63 | 3,37 | 3,23 | 3,13 | 3,00 | 2,93 | 2,86 | |
| 3,48 | 3,22 | 3,07 | 2,97 | 2,84 | 2,77 | 2,70 | |
| 3,26 | 3,00 | 2,85 | 2,76 | 2,62 | 2,54 | 2,46 | |
| 3,11 | 2,85 | 2,70 | 2,60 | 2,46 | 2,39 | 2,31 | |
| 3,01 | 2,74 | 2,59 | 2,49 | 2,35 | 2,28 | 2,20 | |
| 2,93 | 2,66 | 2,51 | 2,41 | 2,27 | 2,19 | 2,11 | |
| 2,87 | 2,60 | 2,45 | 2,35 | 2,20 | 2,12 | 2,04 |
(таблица допускает линейную интерполяцию).
Пример.
Сравнить средние дисперсии содержания KCI в руде 1РУ ПО «Беларуськалий» по данным 1982, 1985гг. :
| 1982г. | 1985г. | |||||
| № | KCI | ∆x1 | ∆x21 | x2 | ∆ x2 | ∆ x22 |
| 28,4 | -0,3 | 0,09 | 26,9 | 0,2 | 0,04 | |
| 29,7 | 1,0 | 1,0 | 26,4 | -0,3 | 0,09 | |
| 28,6 | -0,1 | 0,01 | 26,0 | -0,7 | 0,49 | |
| 28,4 | -0,3 | 0,09 | 25,8 | -0,9 | 0,81 | |
| 28,5 | -0,2 | 0,04 | 25,5 | -1,2 | 1,44 | |
| 29,5 | 0,8 | 0,64 | 27,4 | 0,7 | 0,49 | |
| 29,3 | 0,6 | 0,36 | 0,3 | 0,09 | ||
| 29,2 | 0,5 | 0,25 | 27,3 | 0,6 | 0,36 | |
| 29,7 | 1,0 | 1,0 | 27,4 | 0,7 | 0,49 | |
| 28,9 | 0,2 | 0,04 | 26,7 | |||
| 27,5 | -1,2 | 1,44 | 27,8 | 1,1 | 1,21 | |
| 27,0 | -1,7 | 2,89 | 26,6 | -0,1 | 0,01 | |
| ∑ | 344,7 | 7,76 | 320,8 | 5,52 |
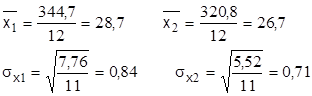
Сравнение средних: 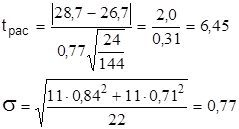
tтабл.(Р=0,95,f=n1+ n2 – 2=22)=2,086
tтабл. <t расч. – следовательно, расхождение значимо с надежностью вывода 0,95. Это значит, что есть объективная причина расхождения, например, изменение качества руды, и , следовательно, объединять в одну выборку данные 1982 и 1985гг. нельзя. 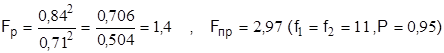
Следовательно, дисперсии свойств (содержание KCI) отличаются незначительно ( точность одна и та же) с надежностью вывода 0,95.
§3.5. Подбор вида эмпирических формул.
Расчет коэффициентов.
Далеко не всегда удается аналитически, опираясь лишь на теоретическое исследование данного процесса, описать необходимую зависимость. В таких случаях основой количественного описания являются экспериментальные данные. Применяют два метода построения эмпирических формул. Один из них состоит в том, что подбирается алгебраический многочлен, принимающий в заданных точках установленные значения, а именно: по наблюдаемым двум точкам строится линейная функция (прямая), по трем - квадратичная (парабола) и т.п. Достоинство метода в том, что полученная формула в точности воспроизводит экспериментальные значения. Такого рода формулы называются интерполяционными многочленами. Способы построения интерполяционных многочленов (Лагранжа, Ньютона, Чебышева) освещены в курсе “Высшая математика” [6]. К недостаткам интерполяционных многочленов следует отнести то, что при большом числе экспериментальных наблюдений многочлен получается высокой степени и нахождение коэффициентов требует громоздких вычислений, а в интервалах между опытными значениями различия между опытной и расчетной зависимостями могут быть как угодно большими. Кроме того, качество математической модели тем выше, чем меньше эмпирических коэффициентов она содержит.
Другой метод подбора эмпирических формул состоит в том, что подбирается наиболее простая формула того или иного вида, во многих случаях содержащая всего два коэффициента, определяемых по экспериментальным данным.
Если при подборе вида формулы удается учесть теоретические представления об изучаемом процессе, то это часто позволяет ограничиться минимумом экспериментальных данных и при этом возможна экстраполяция за пределами проведенных исследований.
В некоторых случаях при подборе вида формулы удается воспользоваться известными заранее соотношениями для скорости процесса (охлаждения, нагревания, фильтрации, диффузии и др.) или данными об угловом коэффициенте касательной к искомой траектории. В табл.3.8 приведены наиболее распространенные случаи скоростей изменения функций и виды их общих закономерностей.
В других случаях вид формул может быть получен при использовании механического (работа, давление и др.) или геометрического (объем, поверхность, дуга и др.) смысла определенного интеграла.
Уравнения в дифференциалах получают в результате составления соотношений между приращениями и переменными. Для этого процесс мысленно разбивают на элементарные акты, позволяющие допустить линейность соотношения между приращениями и переменными, независимость частей целого, применимость фундаментальных законов физики. При использовании материальных или тепловых балансов допускают для элементарного акта или объема независимость потоков субстанций за счет различных движущих сил.
Наиболее надежным и простым является определение коэффициентов a, b линейной зависимости у=ах+b. Применяют один из способов: метод выбранных точек, метод средних и метод наименьших квадратов. По методу выбранных точек выбирают две точки (хо,уо) и (х1,у1), отстоящие достаточно друг от друга и от концов исследуемого интервала. Коэффициенты а,b находятся из
концов исследуемого интервала. Коэффициенты а,b находятся из уравнения:
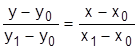
Коэффициенты а,b методом средних находятся из условия равенства нулю алгебраической суммы отклонений экспериментальных n точек от прямой:
Таблица 3.8
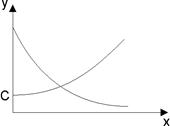
Скорость и общая закономерность некоторых процессов.
| № п/п | Скорость | Закономерность | График зависимости |
 1. 1.
| 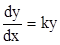
| 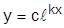
| Экспонента |
 2. 2.
| 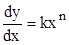
| 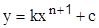
| Степенная зависимость |
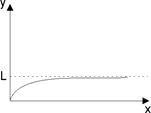 3. 3.
| 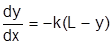
| 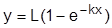
| Асимптота |
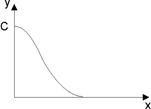 4. 4.
| 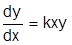
| 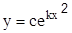
| Кривая вероятностей |
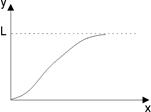 5. 5.
| 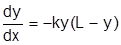
| 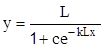
| Кривая Перла |
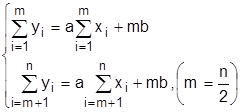
Метод наименьших квадратов является более предпочтительным, так как он требует равенства нулю суммы квадратов отклонений. Параметры a,b находятся из системы:
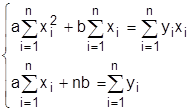
Во многих случаях нелинейные зависимости (степенные, показательные, логарифмические) могут быть приведены к линейному виду с помощью простейших алгебраических действий и замены переменных. Этот метод называется выравниванием функций. Например, зависимость у= аеbx после логарифмирования и замены
lп у=Y приводится к линейному виду Y=lп а +bх.
Зависимость
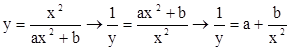
после замены 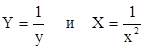
представляется в линейном виде Y = а+bX.
Зависимость
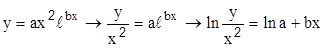
после замены 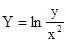 имеет вид Y=lna +bх.
имеет вид Y=lna +bх.
Наиболее полное исследование зависимости требует применения корреляционного и регрессионного анализов. Две случайные величины считаются корреляционно связанными, если математическое ожидание одной из них . меняется в зависимости от изменения другой. Выборочный коэффициент линейной корреляции рассчитывается по формуле:
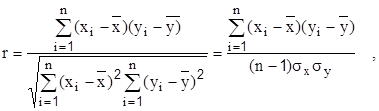
где 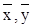 - средние арифметические значения хi, уi;
- средние арифметические значения хi, уi;
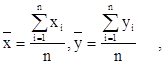
σx,σy - среднеквадратические отклонения;
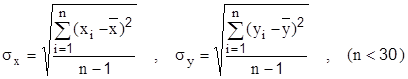
Коэффициент корреляции изменяется в пределах r Є[-1,1]. Знак “минус” - признак обратной связи. Недостаток коэффициента корреляции - его применимость лишь для оценки степени сопряженности величин, связанных линейной зависимостью. Метод выравнивания функций, о котором говорилось выше, позволяет значительно расширить возможности использования коэффициента корреляции для оценки меры тесноты связей. Линейную связь обычно считают слабой, если |г|<0,5, сильной при |г|>0,7 и практически функциональной при |г|>0,9.
В отличие от корреляционной, зависимость между случайной и неслучайной величинами называется регрессионной, а метод анализа этой зависимости - регрессионным анализом. Уравнение линейной регрессии у по х имеет вид:
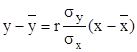 ,
,
где 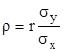 - коэффициент линейной регрессии.
- коэффициент линейной регрессии.
При подборе вида эмпирической формулы удобно пользоват
| <== предыдущая страница | | | следующая страница ==> |
| Математические методы при подготовке и обосновании решений в горном производстве | | | Фрагмент имитационного моделирования работы экскаватора |
Дата добавления: 2014-10-14; просмотров: 509; Нарушение авторских прав

Мы поможем в написании ваших работ!