Уравнения линии в пространстве

Уравнение прямой на плоскости - определение.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.

Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.

Другими словами, уравнение прямой на плоскости в прямоугольной системе координат Oxyесть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.

Осталось разобраться с вопросом, какой вид имеет уравнение прямой на плоскости. Ответ на него содержится в следующем пункте статьи. Забегая вперед, отметим, что существуют различные формы записи уравнения прямой, что объясняется спецификой решаемых задач испособом задания прямой линии на плоскости. Итак, приступим к обзору основных видов уравнения прямой линии на плоскости.

Уравнения линии в пространстве

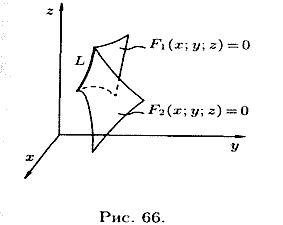
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, об­щих двум поверхностям.

Есл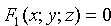и и 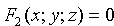— уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

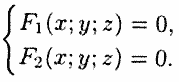(12.1)

Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, 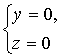есть уравнения оси Ох.

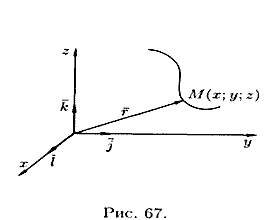
Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

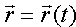
(12.2)

или параметрическими уравнениями

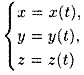
проекций вектора (12.2) на оси координат.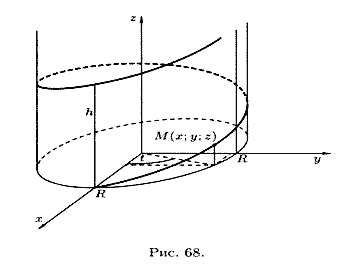

Например, параметрические уравнения винтовой линии имеют вид

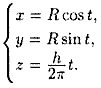
Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

Параметрические уравнения прямой

Замечая, что 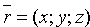, , 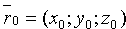, 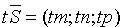уравнение (12.11) можно записать в виде

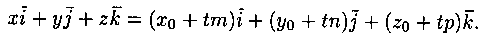
Отсюда следуют равенства:

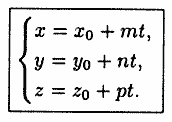(12.12)

Они называются параметрическими уравнениями прямой в пространстве.

Дата добавления: 2014-10-17; просмотров: 598; Нарушение авторских прав

Мы поможем в написании ваших работ!