Общее уравнение прямой

Вид уравнения прямой в прямоугольной системе координат Oxy на плоскости задает следующая теорема.

Теорема.

Всякое уравнение первой степени с двумя переменными x и y вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида .

Уравнение называется общим уравнением прямой на плоскости.

Поясним смысл теоремы.

Заданному уравнению вида соответствует прямая на плоскости в данной системе координат, а прямой линии на плоскости в данной системе координат соответствует уравнение прямой вида .

Посмотрите на чертеж.

С одной стороны можно сказать, что эта линия определяется общим уравнением прямой вида , так как координаты любой точки изображенной прямой удовлетворяют этому уравнению. С другой стороны, множество точек плоскости, определяемых уравнением , дают нам прямую линию, приведенную на чертеже.

Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным. Неполное уравнение прямой вида определяют прямую, проходящую через начало координат. При А=0уравнение задает прямую, параллельную оси абсцисс Ox, а при В=0 – параллельную оси ординат Oy.

Таким образом, любую прямую на плоскости в заданной прямоугольной системе координатOxy можно описать с помощью общего уравнения прямой при некотором наборе значений чисел А, В и С.

Нормальный вектор прямой, заданной общим уравнением прямой вида , имеет координаты .

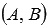Все уравнения прямых, которые приведены в следующих пунктах этой статьи, могут быть получены из общего уравнения прямой, а также могут быть обратно приведены к общему уравнению прямой.

Рекомендуем к дальнейшему изучению статью общее уравнение прямой. Там доказана теорема, сформулированная в начале этого пункта статьи, приведены графические иллюстрации, подробно разобраны решения примеров на составление общего уравнения прямой, показан переход от общего уравнения прямой к уравнениям другого вида и обратно, а также рассмотрены другие характерные задачи.

4Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид 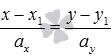, где и – некоторые действительные числа, причем и одновременно не равны нулю.

Очевидно, что прямая линия, определяемая каноническим уравнением прямой, проходит через точку . В свою очередь числа и , стоящие в знаменателях дробей, представляют собой координаты направляющего вектора этой прямой. Таким образом, каноническое уравнение прямой 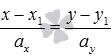в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку и имеющей направляющий вектор .

Для примера изобразим на плоскости прямую линию, соответствующую каноническому уравнению прямой вида . Очевидно, что точка принадлежит прямой, а вектор является направляющим вектором этой прямой.

Каноническое уравнение прямой вида 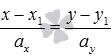используют даже тогда, когда одно из чисел или равно нулю. В этом случае запись 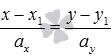считают условной (так как содержится ноль в знаменателе) и ее следует понимать как . Если , то каноническое уравнение принимает вид и определяет прямую, параллельную оси ординат (или совпадающую с ней). Если , то каноническое уравнение прямой принимает вид и определяет прямую, параллельную оси абсцисс (или совпадающую с ней).

Параметрические уравнения прямой на плоскости имеют вид , где и – некоторые действительные числа, причем и одновременно не равны нулю, а - параметр, принимающий любые действительные значения.

Параметрические уравнения прямой устанавливают неявную зависимость между абсциссами и ординатами точек прямой линии с помощью параметра (отсюда и название этого вида уравнений прямой).

Пара чисел 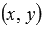, которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра , представляет собой координаты некоторой точки прямой. К примеру, при имеем , то есть, точка с координатами 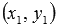лежит на прямой.

Следует отметить, что коэффициенты и при параметре в параметрических уравнениях прямой являются координатами направляющего вектора этой прямой.

Для примера приведем параметрические уравнения прямой вида . Эта прямая в прямоугольной системе координат Oxy на плоскости проходит через точку с координатами 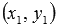и имеет направляющий вектор .

Дата добавления: 2014-10-17; просмотров: 443; Нарушение авторских прав

Мы поможем в написании ваших работ!